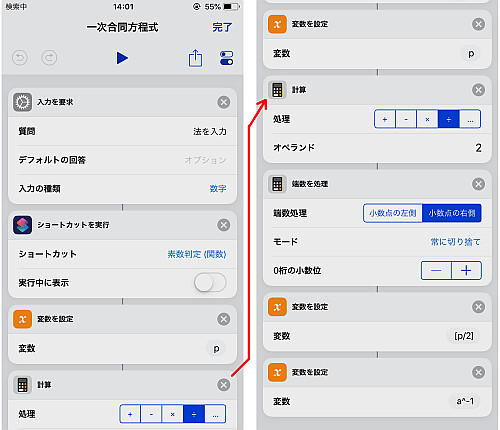
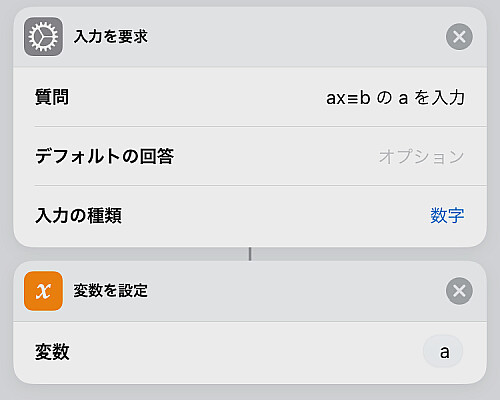
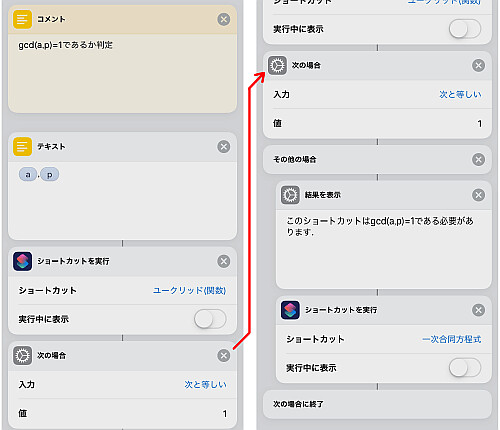
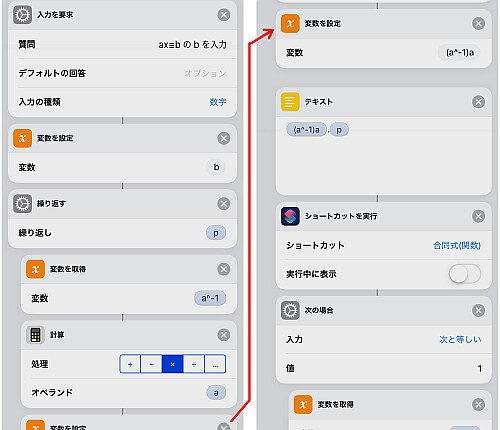
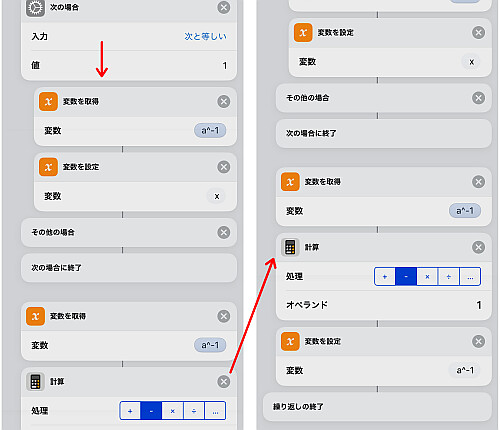
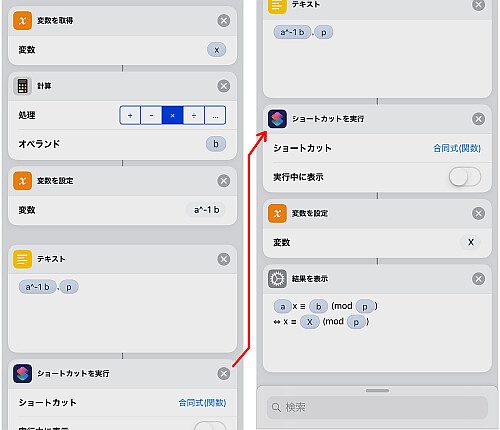
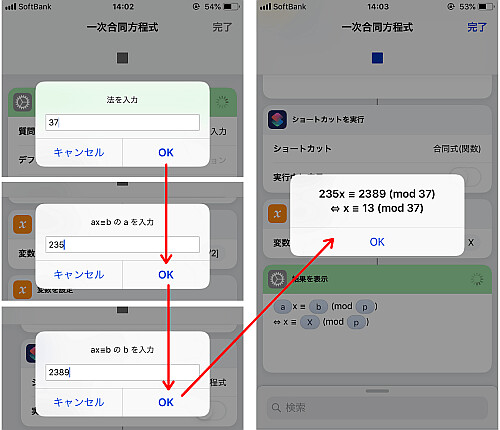
指数表を作るためには,  という形の数をひたすら法で整除しなければなりません.
という形の数をひたすら法で整除しなければなりません.
なのでその作業をできるだけ減らしたい, それが今回の目的です.
スポンサーリンク
指数表作りに必要な定理たち
原始根および指数表について, 過去にも面白い性質を見つけましたが何だかんだその証明にもたどり着けました.
未証明が一つありますが既知のもを含め必要なものを紹介しましょう.
なお, 本記事ではpを5以上の素数とします.
「素数pについて~」とある場合でも2と3は無視します, 定理によってはp=3でも成り立ちます.
定理1
これは原始根を学ぶ際に触れる既知のものです.
定理2
 ですから,
ですから,

によって成り立ちます.
ようは, 指数表の真ん中を軸にした両端の値の差の絶対値を取ったものが必ず となります.
となります.

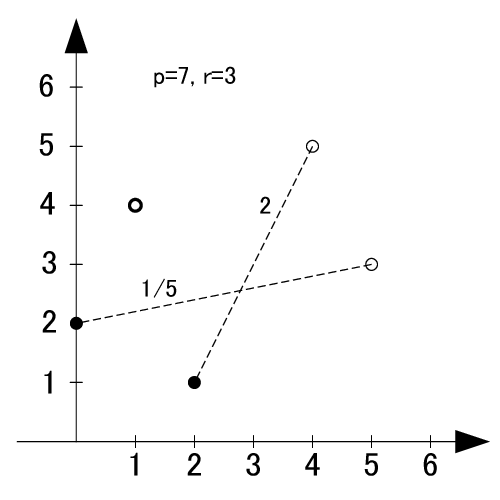
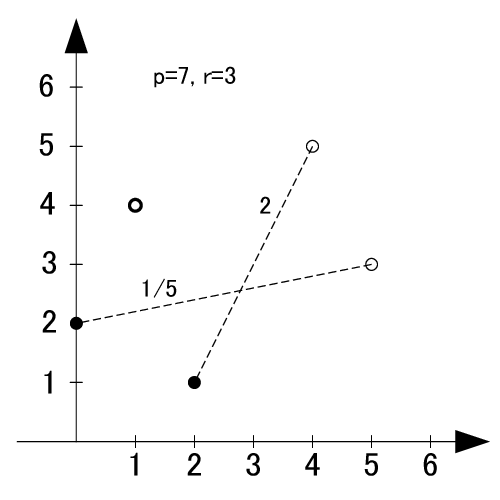
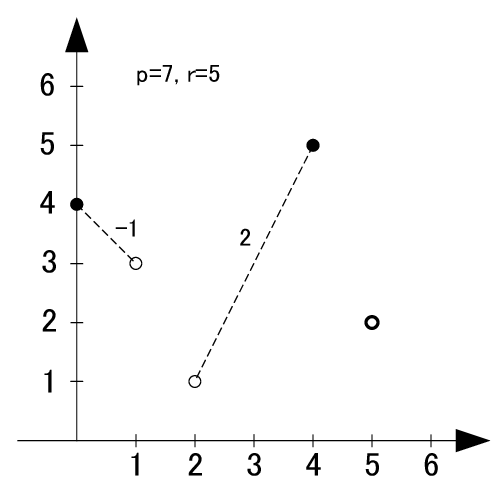
参考までにp=7の場合を見てみます.
p=7の場合はp-1=6項あるわけですが, その真中である3と4を軸にその両端の差を取り更に絶対値を取るとそれぞれ
|0-3|=3 |2-5|=3, |1-4|=3
|0-3|=3, |4-1|=3, |5-2|=3
とすべて3になっています.
推論3
上で紹介したp=7の指数表を縦に見ると, それぞれの偶奇は全部同じですね.
少なくともp=37までの指数表については確認しています.
今回の目的で必須ではありません.
定理4
これは原始根の定義から比較的簡単に導かれます.
素数 の任意の原始根
の任意の原始根 はフェルマーの定理より
はフェルマーの定理より

を満たします.
 ですから法はそのままに両辺を
ですから法はそのままに両辺を で割れるので
で割れるので

, よって の解が
の解が に相当します.
に相当します.
 は原始根の定義より明らかですから, この合同方程式に解が存在することも明らかです.
は原始根の定義より明らかですから, この合同方程式に解が存在することも明らかです.
ではこの は原始根なのか…という疑問が生じます.
は原始根なのか…という疑問が生じます.
しかしこれは定理1より,  が明らかであることから簡単に分かります.
が明らかであることから簡単に分かります.
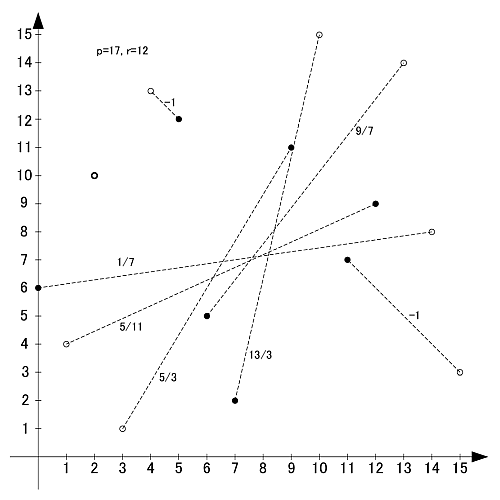
今回の定理の例をp=17で見ると, 原始根は3,5,6,7,10,11,12,14の8つですがうまく組み合わせることで

であることが分かります.
ただ肝心の1が原始根でないため, 代数学的には準群(quasi-group)に相当するんでしょうかね.
乗法可換なのは明らかですから, このような と
と のペアは1対1です.
のペアは1対1です.
素数 に対する原始根の個数は
に対する原始根の個数は であり, かつ3以上の自然数nについて
であり, かつ3以上の自然数nについて は2を約数に持ちますから, 指数表の項数は偶数, 従って任意の原始根はいづれかのペア
は2を約数に持ちますから, 指数表の項数は偶数, 従って任意の原始根はいづれかのペア の一方となり, 即ち原始根による集合はこのペアによって類別されます.
の一方となり, 即ち原始根による集合はこのペアによって類別されます.
このペア を本記事では「r-set」と呼ぶことにします.
を本記事では「r-set」と呼ぶことにします.
系5
定理4を整理しただけです.
仮に原始根の値が小さくても を整除するのは面倒ですから2つ目は計算を前提とすると必要のないものです.
を整除するのは面倒ですから2つ目は計算を前提とすると必要のないものです.
定理6
指数についての定理

より,

, よって .
.
指数 は法
は法 において合同関係にあるため,
において合同関係にあるため,  となります.
となります.
また(*)はr-setの定義より より
より が成り立つことを利用しています.
が成り立つことを利用しています.
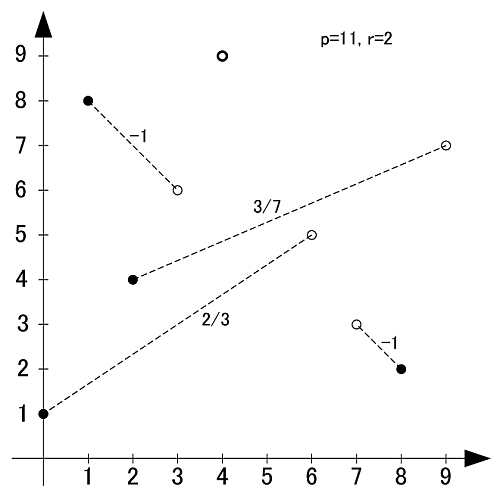
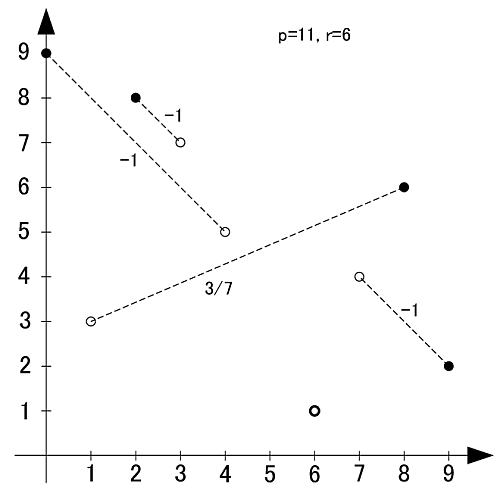
定理2は固定の原始根に基づく「横の関係」でしたが, こちらは固定の自然数に対する「縦の関係」です.

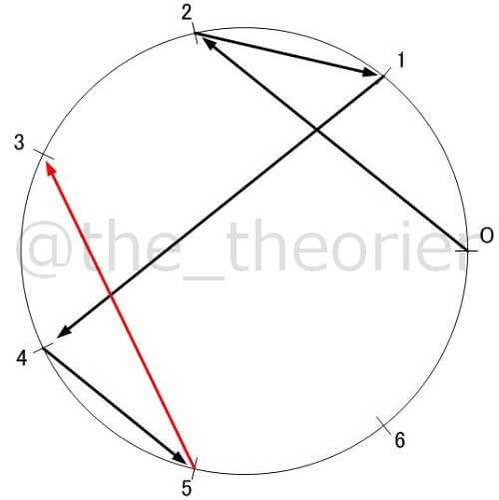
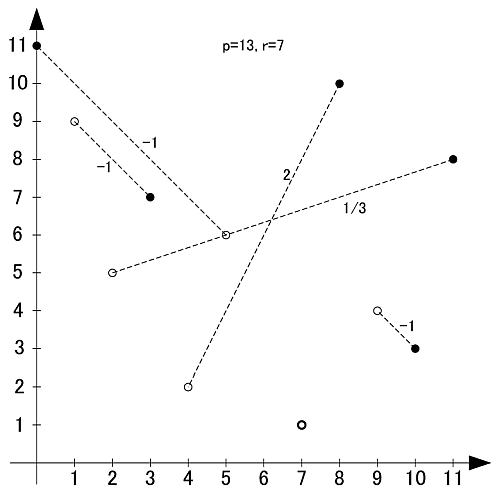
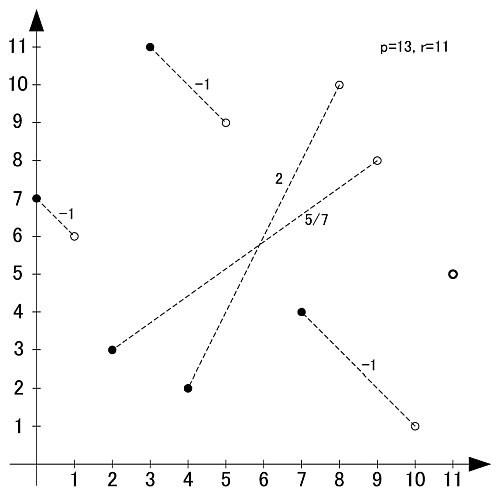
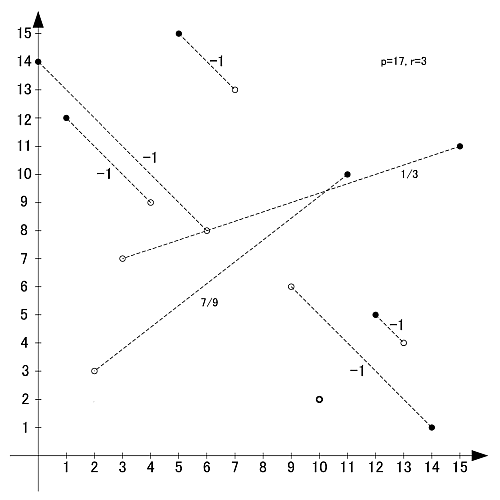
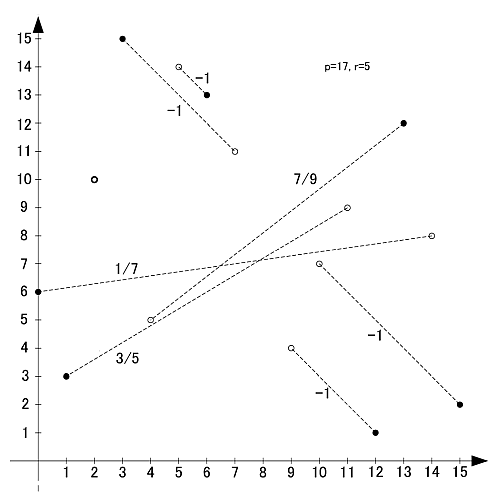
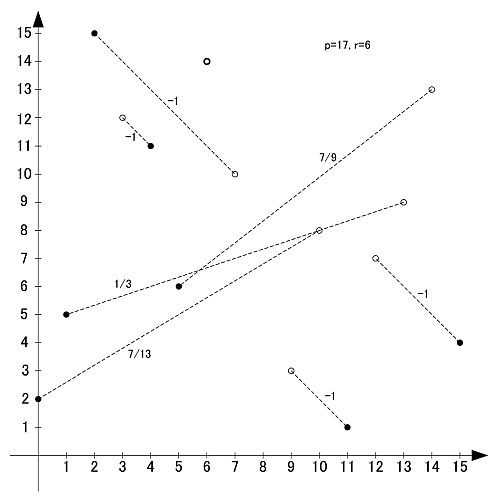
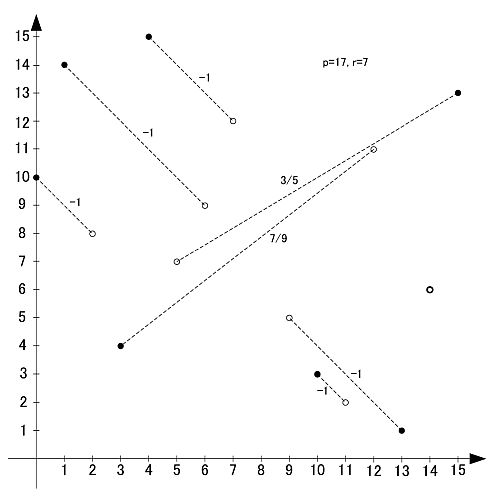
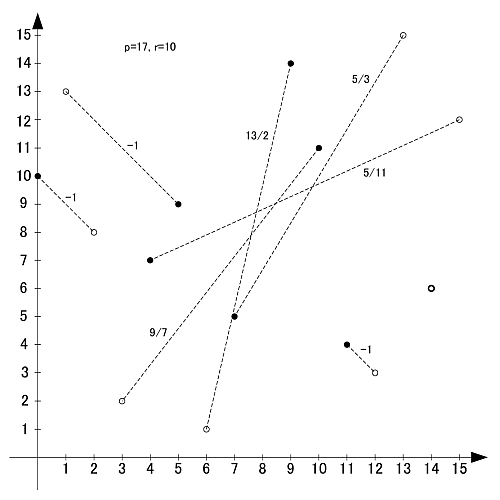
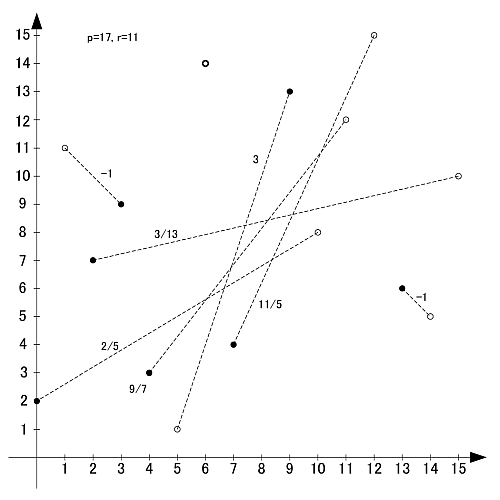
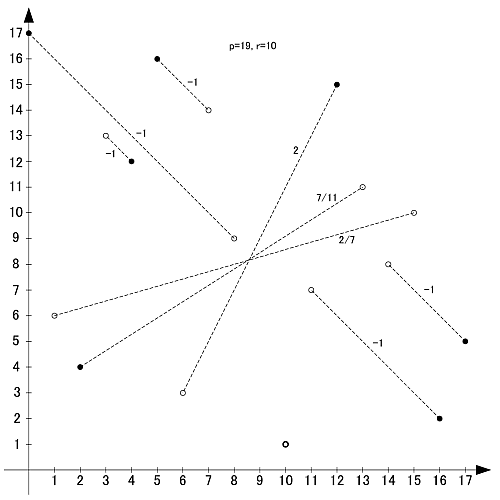
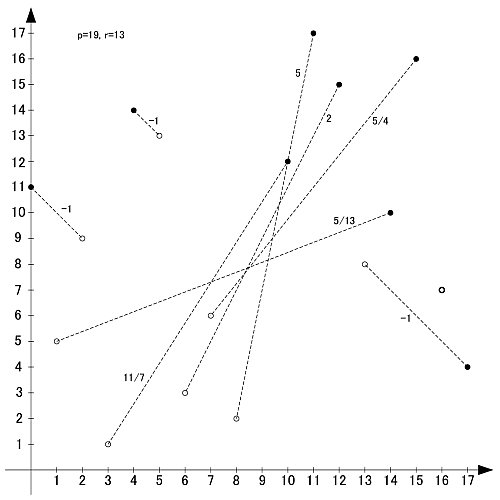
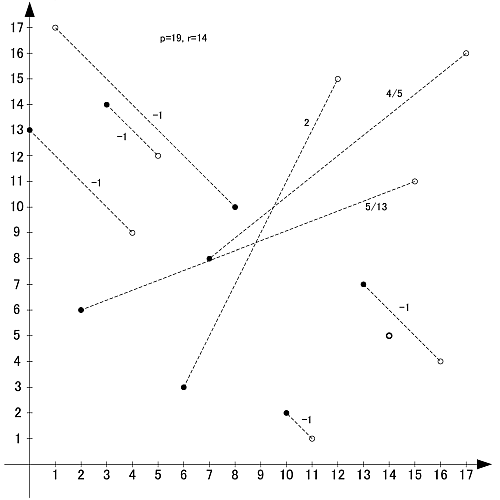
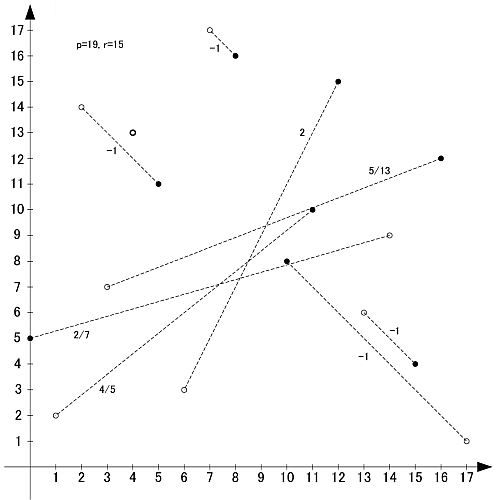
画像のように, r-set同士の値を足し合わせると,  と合同になります.
と合同になります.
準備は以上です, ここから具体的に指数表を組んでみます.
指数表作り
大まかな流れとしては, まずひとつでも良いので原始根を見つけ, 残りの原始根は定理1を使います.
続いて定理4の後に書いたように

を解くことでr-setを組みます.
後は容易な累乗を優先して項目を追加し, そのたびに定理2と6を駆使して埋めていきます.
p=17での例
試しにそれなりの難易度であるp=17でやってみましょう.
準備
素数17の原始根は3,5,6,7,10,11,12,14の8つです.
一つ見つければあとは定理1を使って芋づる式に見つかります.
 が原始根であるためには
が原始根であるためには である必要があるのと, 計算のしやすさから
である必要があるのと, 計算のしやすさから や
や などがどうなるか試します.
などがどうなるか試します.
続いてr-setを組みます.
定理4で紹介したとおり, 法17について

ですから, p=17のr-setは(3,6),(5,7),(11,14)の3組です.

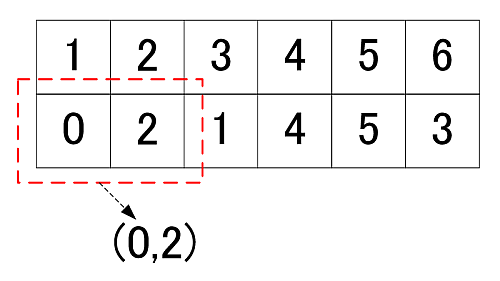
では分かるモノから入れてみます.
左の背景色はr-set, n=8,9の背景色は表の中央を表しています.
n=1の場合は自明, n=16についても先程の  から, 原始根に関係なく
から, 原始根に関係なく であることがわかります.
であることがわかります.
また も自明ですからこれも簡単に埋められます, これによって定理2より
も自明ですからこれも簡単に埋められます, これによって定理2より を埋めることもできます.
を埋めることもできます.

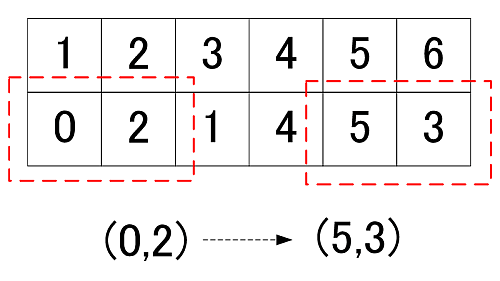
値1と9が埋まったので, 定理6より対応するr-setの値も埋めることができます(以降、背景が赤い場所が追加した部分).
今回はp=17なので, 足して17になるように, r-setの片方の値が定まります.
累乗の計算なしで埋められるのは, 今回はここまでです.

仕方ないので2乗の値を計算して埋めていきます.

なので, 上画像のように値2が埋まります.
 はそれぞれ法17について
はそれぞれ法17について と合同ですからこれも利用します.
と合同ですからこれも利用します.

追加した値2に対して, 定理2より値 を埋めることができます.
を埋めることができます.

追加した2と10に対して, 定理6より と
と が埋まります.
が埋まります.
まだ足りないので仕方ないです, 3乗も計算しましょう.


より, 上画像のように値3が埋まります.

追加した値3に対して, 定理2と6より, 値5,11,13を埋めることができます.
これであとは4と12だけになりました.

これまでの流れを見て分かった方も居られるでしょうが, あと4ヶ所埋まればすべて埋められます.
計算のしやすさを考えて3,5,12,14の4乗を計算します.

なので上画像のように埋まります.

残りはやはり定理2と6を使います.
これでp=17の指数表が完成しました.
〆
定理2と6のお陰で一つ確定するとその縦と横の1つずつが確定するため, 作業効率が格段に減ることとなります.
すべての累乗を計算する手間を考えれば, 今回の例だと素数17に対して8つの原始根の15乗までを計算するのは面倒ですね, それが4乗の一部までで済むことになるのですから.
本当は指定の原始根に対する指数表を簡単に作りたいというのが目的だったので回り道をしているように思えますが現状はこれが早いですね.