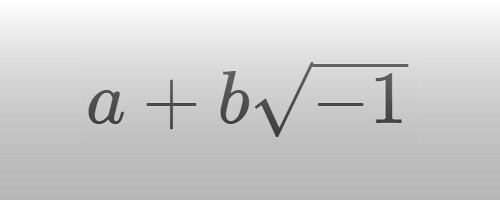
質問サイトでも, 質問者に限らず回答側ですらそのように評価している方がとても多いです.
0の定義
そもそも何を以て0とするかも, 詳しく掘り下げればキリがないですが, 取り敢えず代数学をもって説明することにします.
集合 による直積
から
への写像
が存在するとき, を
の2項演算,
を
の積(掛け算の積ではありません), また「
は2項演算
に関して閉じている」「
は亜群をなす」と言います.
(この時点で は加法とも乗法とも言っていません)
この亜群 が以下を満たすとき,
はモノイド(または単位的半群)と呼び,
を単位元と呼びます.
(1)結合律
の任意の元
について
.
(2)単位元
の任意の元
について
を満たす元 がただ一つ存在する.
とくに, 2項演算 が加法である場合,
を「零元」と呼びます.
この零元が, 一般的に に相当します.
代数学では代数系次第で であることがありうるので軽々に
と決めつけることはしません.
0に実在の要素はあるのか
このように, 数学における というのは対象の集合
における元として存在します.
が存在しない数云々というのは過去にそれが発見, 発明された当時の話であり, 当時は純粋な数学の範疇を超えた解釈がされることがしばしばありました.
特にヨーロッパでは, 数の概念として
- 序数
- 基数
- 量
に関して厳密に区別していました.
例えば1個, 1日, 1…といったものを区別するべきかどうか…という話ですね.
は存在しないものであり, よって例えば
が
であると見なす時代もありました1.
対して東洋ではこのような区別はせず, 比較的寛容に扱っていたようです.
時期や地域によっては, はもちろん負数についても, どのように扱うべきか長い年月をかけて様々な考えがあり, 移り変わっていきました.
逆に言えば当時の解釈が現代数学のそれであるとは限らない…とも言えます.
インドで初めて が生まれた…というのは有名な話ですが, 当時の考えが全く変わらずそのまま今も受け継がれているわけではなく, その他もまた同様です.
たまに流行る「」の根拠を電卓で示す方がいますが, このようにプログラムで好きに解釈できるようなもので, 結局は「どのように扱うべきか」が全てです.
初めから結論が決まっているのであれば発見して研究した所で既に「分かっている」はずです.
時間と手間されあれば限りなく真実に近づくことのできる科学と違い, 数学はルール作りの時点で好きにできます, 矛盾していなければですが.
故 高木貞治氏は著書「数の概念」でこのように主張しています.
~我々の整数は,物の数でもなく,物の順序を示すものでもない.し かし,物の数を示すためにも,物の順序を示すためにも,なお一般に, 物の標識(符牒)としても用いられる.0 は加法の基準として,我々が 任意に整数の体系の中から取り出した一つの整数である.それは,無 を示すものではない.~中略~ 事実は,我々が常用の言語に順応して, 我々の記号 0, 1, 2 を零,一,二と呼ぶことにしたのである.~
ここで述べている「我々」とは数学者, 或いは数学を学ぶ立場ということです.
この解釈は, 数概念として自然数から始めるのでなく, 整数から評価しているということです.
数学における「数」というのは, まず数学の世界で作ったものに過ぎず, しかしそれを日常で使われている数や量の表現に, 言ってみれば「翻訳することもできる」と言えます.
後述の虚数でもそうですが, 現代数学の各種体系が日常に応用できることこそあれ, この2つをイコールとすることは出来ないことが多いことに注意してくれだい.
これは以前投稿した絶対値と距離の「イメージ」と似ています.
日常での常識やイメージがそのまま数学に繋がるとは限りません.
虚数単位の定義
次は虚数です.
まず虚数単位から見てみましょう.
2次方程式
の根の一つを, 虚数単位と言い, の記号で表すことが多いです.
2次方程式なので今は高々2つ存在するわけですが, どちらを虚数単位とするかは一般的に定義に含まれません.
しかし通常は2根 のうち前者を選ぶことが殆どです.
そもそも「存在する」とはどういうことか
数が存在する, 実在するってそもそもどういうことなんでしょうか?
文字で書けることでしょうか?でもそれなら虚数だって のように書けますね.
長さや量といった指標で表せないから…という考えもありますが, 先の通り, (現代)数学は矛盾さえしていなければ, 現実に則しておらずとも構わない…そんな世界です.
一つ考えるならば, その「拡張」を考えた上で, その定義で良いかどうか…でしょうか.
結局のところ, 僕たちは例えば 1 とか 2 といった数の実在を証明することはできません.
できることは
実在する何かで置き換えること
です.
何かとは例えば文字(記号)であったり, 或いは数えられるような対象, または液体のような量として測れるモノです.
1 にしても, 例えば漢字ならば一ですし, 英語ならばoneです.
つまり一つの数を表すにしても様々な方法があります.
数とは飽くまでも「概念」として存在・実在するのであり, 従って我々がそれ自身を, 記号や例え以外によって目に見える形で示すことはできないのです.
そしてこれに基づけば虚数も同じではないでしょうか?
例えば2次元ユークリッド空間と複素空間は, 各々の と
を対応させることで同一視させることができます(扱う「道具」次第では不可能).
つまり「翻訳」次第では概念として「実在を確かめる」ことができるわけですね.
ある意味では, これは「言葉が実在することは証明できるのか?」という問題と同じなのです.
あなたは「言葉」が存在することを, どのように証明しますか?
そしてその証明法は数の実在と違いはあるでしょうか?
方程式の解
我々は学校で当たり前のように二次方程式の解を, 或いは公式として学びます.
これも発明された当時は実数解とならない例があるのをめぐって賛否あったケースがありました, 「考えないことにする」こともあったそうで.
もっと遡れば で負数解が, 或いは解が
になる場合はどうするべきなのか…と, 「実在を認めないことによる不都合」はそのたびに起こりました.
つまるところ「不都合なら認めちゃおう」, それが, 各々の黎明期に「認めなかった」西洋の考えだったようです.
東洋の場合は早々にその存在を受け入れたため, そもそも認めるも認めないも, それこそ実在がどういうという問題・議論に至らなかったわけですね.
内部対称性
「実在しない」と決め込むよりも, それを受け入れた方が都合がよいことがあります.
二次方程式の解の公式はその分かりやすい例の一つでしょう, 虚数解が生まれる可能性があるからとして否定するのは勿体ないことです.
複素数では「複素共益」という概念があります, 例えばある二次方程式
の解の一つが であるとき,
も解ですね.
もっとシンプルに, そもそも虚数単位の定義で の解(根)のどちらを虚数単位とするかに明確な定義がないことを先程書きました.
この複素共益は特に実数係数2次方程式で評価することが多いですが, つまるところここにおいて と
, もっとシンプルに
と
に明確な区別がなく曖昧な存在となっています.
この相対する関係は対称性と言われています.
我々のイメージするところの「観測できる値」は実数までであり, これに基づけば虚数は「観測できない値」です.
ここで我々が何かを行うとき, 果たして「観測できる値」の世界だけで余すことなく議論できるでしょうか?
特に二次方程式の解, いや実数解を考える際, 各実係数 がどのような数であっても, 虚数の世界に立ち入らずにできるでしょうか?
勿論できる場合もありますし, ちょっと難しくても強引にやれば可能かもしれません.
しかしそのとき, 虚数という「観測できない値」の存在を認めて, つまり解の公式をまるっと認めてしまった方が楽だと思いませんか?しかも結果的に虚数が現れないのであれば…
このように, 観測できない値(空間)を認め, 含んだ上で議論する(できる)性質を内部対称性と言います.
物理や科学などで一時的にでも虚数単位が登場するのはまさにこの内部対称性の考えを使っているからです.
二次方程式の解の公式も, 一つ一つは虚数解が現れる事がなくとも, 「一時的に現れることを想定して」, 実数の世界に縛られず, 複素数の世界で評価するわけです.
〆
つまるところ, 0や虚数の実在を証明することはできません.
しかしそれは言語がそうであることと同じで「概念としての実在」でしか我々は確認できないのと同じということです.
1 : 一般社団法人 日本数学会 「高木貞治に見る数学思想の変遷」足立恒雄 (早稲田大学理工学術院)

