もう一人のY君

iPhoneアプリのレビューやアップデートレビューなどを書いています. たまに数学の記事も書きます.

もう一人のY君　MENU 　MENU

拡張ユークリッドのアルゴリズム

数学

　こんにちは, @the_theorierです.

 

　時間が出来たので拡張ユークリッドも書いていこうと思います.

 

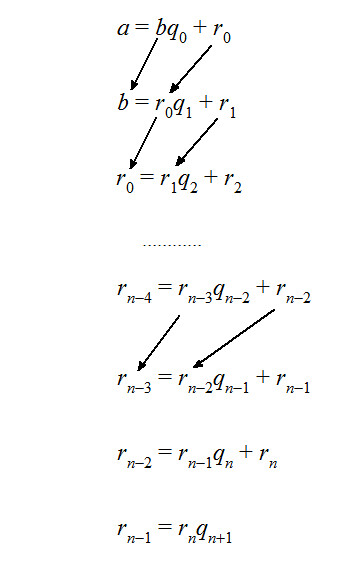
 130222_03

 　昨日の通りで, 2つの正整数 a, b を使って a = bq + r と分解する行為を繰り返すことで, a, b の最大公約数を得るのがユークリッドの互除法でした.

 

thetheorier.hatenablog.com

 

 　拡張ユークリッドではここで使った式変形を利用します.

 

　上にある式たちを, 最後だけ除いてすべて r = ～ の形にします.

 

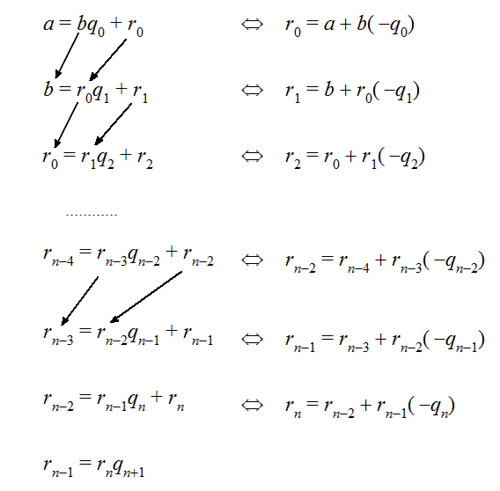
 130222_04

 　こんな感じです.

 

　ここで右側の最後の式を, その上の式に代入して整理します.

 

{ \displaystyle r_{n} = r_{n-2} + \{ r_{n-3} + r_{n-2} (-q_{n-1})\}\times (-q_{n}) }

{ \displaystyle ⇔　r_{n} = r_{n-3}(-q_{n-1}) + r_{n-2}(1+q_{n-1}q_{n}) }

 

　余りの列 { \displaystyle r_{n} } を変数, { \displaystyle q_{n} } を定数と見做して扱うのがポイントです.

 　ここで

 

{ \displaystyle A = -q_{n-1} }

{ \displaystyle B = 1+q_{n-1}q_{n} }

 

とでも置けば, 二つはやはり定数であり, 上の等式は

 

 { \displaystyle r_{n} = r_{n-3}A + r_{n-2}B }

 

と書けます.

 

 　はじめの { \displaystyle r_{n} = r_{n-2} + r_{n-1}(-q_{n}) } の時点では, { \displaystyle r_{n} } は「{ \displaystyle r_{n-2} } と { \displaystyle r_{n-1} } の線形和」で表されていますが, 上では「{ \displaystyle r_{n-3} } と { \displaystyle r_{n-2} } の線形和」で表されていますね.

 

 　同じことを今度は最後から3つめの式を代入すれば, 今度は { \displaystyle r_{n-3} } と { \displaystyle r_{n-2} } の線形和になることはもう明らかです.

 

 　これをどんどん繰り返せば, 最終的に a と b の線形和になるわけです, つまりある定数 { \displaystyle x_{0}, y_{0} } が存在して

 

{ \displaystyle ax_{0} + by_{0} = r_{n} }

 

 となるわけです.

 　この { \displaystyle x_{0}, y_{0} } の組は一次不定方程式 { \displaystyle ax + by = r_{n} } の解の一つに他なりません, 一般的にこのようにして得られた解は「特殊解」と呼ばれます.

 

 　あとは一般解を求めるだけです, つまり特殊解は元々の不定方程式の解の一つですから, 

{ \displaystyle ax_{0} + by_{0} = r_{n} }

 を満たしています.

 　これと元の一次不定方程式 { \displaystyle ax + by = r_{n} } から辺々引いて整理すると,

 

{ \displaystyle (ax + by) - (ax_{0} + by_{0}) = r_{n} - r_{n} }

{ \displaystyle ⇔　a(x - x_{0}) + b(y - y_{0}) = 0 }

{ \displaystyle ⇔　a(x - x_{0}) = b(y_{0} - y) }

 

 …となりますね.

 　これはつまり,

 

  • { \displaystyle x - x_{0} } は b の倍数
  • { \displaystyle y_{0} - y } は a の倍数

 

 を意味しています, 従って上の2つは整数 k を用いて

 

{ \displaystyle x - x_{0} = bk }

{ \displaystyle y_{0} - y = ak }

 

と書きかえることができます, これを整理して

 

{ \displaystyle x = bk + x_{0} }

{ \displaystyle y = -ak + y_{0} }

 

となります, { \displaystyle x_{0}, y_{0} } は特殊解だったのでなんらかの定数です.

 

　こうして特殊解 { \displaystyle (x, y) = (x_{0}, y_{0}) } から一般解 { \displaystyle (x, y) = (bk+x_{0}, -ak+y_{0}) } を得ることが出来ました.

thetheorier