もう一人のY君

iPhoneアプリのレビューやアップデートレビューなどを書いています. たまに数学の記事も書きます.

もう一人のY君　MENU 　MENU

【ショートカット】円周率の近似値を求める【モンテカルロ法】

iOS iOS-iOS12 iOS-ショートカット

181110_00

　ショートカットアプリには乱数を発生させるアクションがあります.

　そこで乱数を用いて円周率を求めるショートカットを作ってみます.

 

ショートカット

ショートカット

  • Apple
  • 仕事効率化
  • 無料

※価格は記事執筆時のものです. 現在の価格はApp Storeから確認ください.

　レビュー時のバージョン　：　v2.1.1

 

スポンサーリンク

 

 

　モンテカルロ法

　円周率の近似値を求める手法は色々ありますが今回はモンテカルロ法を用います.

 

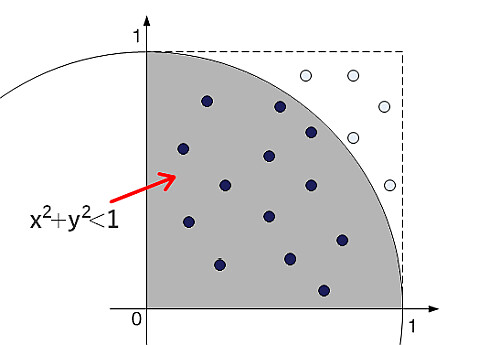
181110_01

　モンテカルロ法による円周率の求め方は, 画像のように点 (0,0), (0,1), (1,0) を頂点とする正方形にランダムに点を置き, その点が { \displaystyle x^2+y^2\lt 1 } の中にどれだけ入るか…でおよその円周率を求めます.

　もし画像の通りなら正方形全体では17個, うち { \displaystyle x^2+y^2\lt 1 } に収まっている点は13個なのでその割合は { \displaystyle \frac{13}{17} } です.

　半径 { \displaystyle 1 } の 円の面積は { \displaystyle \pi } であり, 範囲 { \displaystyle x^2+y^2\lt 0,\, x\geq 0,\,y\geq 0 } はその { \displaystyle \frac{1}{4} } ですから結果に { \displaystyle 4 } をかけて { \displaystyle 4\times\frac{13}{17} \approx 3.0588\dots } となります.

 

　整理すると { \displaystyle 0\leq x\lt 1 ,\, 0\leq y\lt 1 } に置いた乱数全体の個数を { \displaystyle N } , そのうち { \displaystyle x^2+y^2\lt 1,\,x\geq 0 ,\, y\geq 0 } に収まる点の個数を { \displaystyle n } とすると, 円周率 { \displaystyle \pi } は

 

{ \displaystyle \pi\approx 4\frac{n}{N} }

 

と推定できます.

 

　当然 { \displaystyle N } の値が大きければ大きいほどより { \displaystyle \pi } に近い値が得られる可能性が大きいです.

 

　そこで今回は乱数を用いて { \displaystyle 0\leq x\lt 1 } となるような数の組を2つ用意し, 各々の { \displaystyle 2 } 乗の和が { \displaystyle 1 } より小さいかどうかを確かめることになります.

 

 

フロー

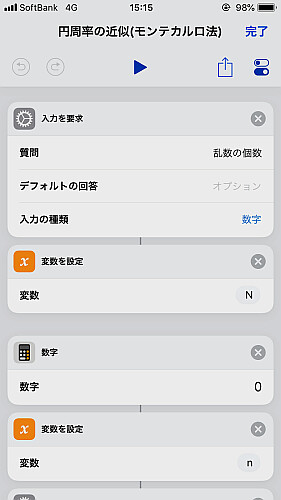
181110_02

　というわけでフローを組んでみましょう.

　まず乱数の個数を要求し, 適当に変数 N に代入します.

　繰り返し用に初期値 0 の変数 n も用意しておきます.

 

 

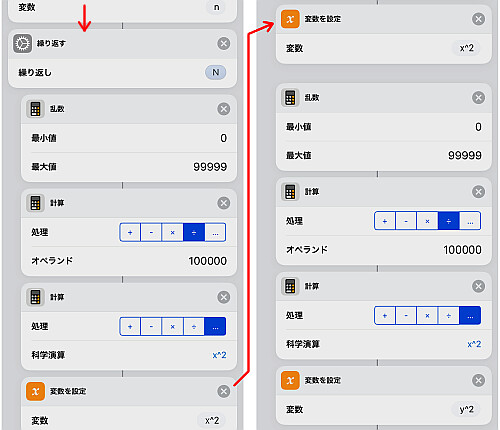
181110_03

　「繰り返す」のアクションを入れ, 乱数を２つ作ります.

　但しショートカットアプリでは乱数については整数でしか出せません.

　従ってまず整数で乱数を発生させ, それを設定した最大値で割ることによって区間 { \displaystyle [0,1) } の乱数に変換します.

　精度を大きくするには最大値をできるだけ大きく取った方が良いでしょう.

　今回は { \displaystyle x^2+y^2\lt 1 } としたので敢えて乱数の最大値を99999, 割る数を100000としています.

　2乗して足すことが分かっているため直ぐに2乗し, これを変数として置きます.

　{ \displaystyle x^2,\,y^2 } の2つ分作りましょう.

 

 

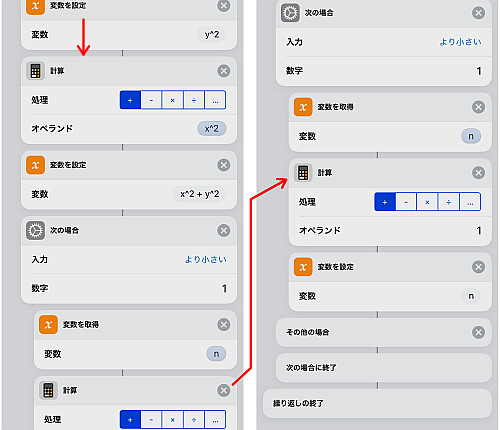
181110_04

　{ \displaystyle x^2+y^2 } を計算し, 「次の場合」アクションで { \displaystyle 1 } との大小を比較し, 小さければ先程の変数 n に 1 を足し, そうでなければ何もしません.

 

 

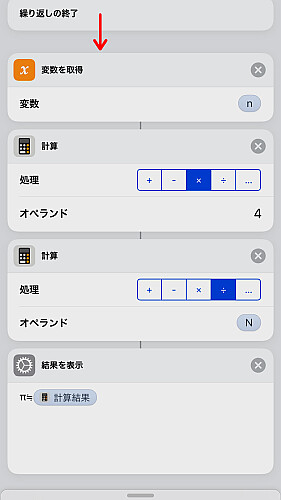
181110_05

　繰り返しが終わったら一度変数 n を呼び出し, はじめに要求した乱数の個数 N と 4 を掛け合わせば完了です.

 

 

実行

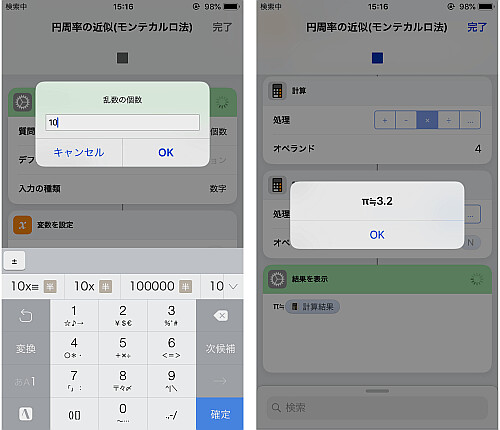
181110_06

　実際に実行してそれらしい結果になることを確かめます.

　処理するたびに乱数が異なるため, 個数が同じでも結果は同じとは限りません.

 

 

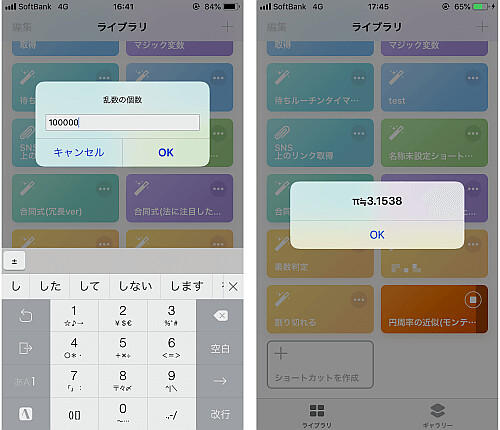
181110_07

　100000のような大きな数でも意外と正確にはならないものです.

　画像の通り処理自体もとてもかかっています, ショートカットアプリは使用メモリの制約や余計なアクションもあってあまり高速な処理は期待できないと思ったほうがいいです.

 

 

〆

　乱数は仕様のままでは整数でしか使えないため, 上記のように最大値で割るなどの工夫をすることである程度自由な使い方ができるようになります.

 

　とはいえ乱数をまともに使うならせめて4桁個くらいまでは待たされることなく終わるように作りたいものです.

　例えば今回のショートカットでも, 乱数500個で約16秒もかかってしまいます.

　内容次第ではもっと複雑になりうるでしょうから, それ以上はショートカットに期待するのは難しく, 餅は餅屋ということになってしまいます.

 

 

thetheorier