もう一人のY君

iPhoneアプリのレビューやアップデートレビューなどを書いています. たまに数学の記事も書きます.

もう一人のY君　MENU

【ショートカット】素数判定をするショートカット

iOS iOS-iOS12 iOS-ショートカット 数学

181103_16

　今回は先日紹介した割り切れるかどうかを判定するアイデアを素数判定に利用します.

　なお今回も「自然数」のことを「正整数」として扱います.

 

ショートカット

ショートカット

  • Apple
  • 仕事効率化
  • 無料

※価格は記事執筆時のものです. 現在の価格はApp Storeから確認ください.

　レビュー時のバージョン　：　v2.1

 

スポンサーリンク

 

 

素数判定のアイデア

　まずは素数の定義から振り返りましょう.

 

　自然数 { \displaystyle m } は { \displaystyle 1 } と { \displaystyle m } という, 少なくとも2つの「自明な(正)約数」を持ちます.

　なお { \displaystyle 0 } は自分自身を除く任意の自然数を, そして { \displaystyle 1 } は自分自身ただ一つを正約数に持つ特殊な数です.

　自然数 { \displaystyle m\,(\gt 1) } の中には自明な約数以外の正約数があります, これを「真の約数」と言います.

　自然数 { \displaystyle m } が真の約数を持たないとき, { \displaystyle m } を素数, 真の約数を持つとき合成数と呼びます.

 

　素数 { \displaystyle p } は自明な正約数を持ちませんから, 先日の「割り切れる」に倣えば

 

{ \displaystyle \frac{p}{2},\,\frac{p}{3},\,\dots,\,\frac{p}{p-1} }

 

の { \displaystyle p-2 } 個はいずれも整数ではありません.

　但し { \displaystyle p=2 } はこの限りではないためここからは { \displaystyle p } を奇素数とします.

 

　加えて自然数 { \displaystyle m} は高々　{ \displaystyle \sqrt{m} } までの自然数で割り切れます.

　仮に自然数 { \displaystyle m } が2つの自然数　{ \displaystyle a,b\, (a\leq b) } の積と等しいとき,

 

{ \displaystyle m=ab \\ \Rightarrow \, m\leq a\times a = a^2 \\ \Leftrightarrow \, \sqrt{m}\leq a }

 

により,　{ \displaystyle m } の約数　{ \displaystyle a } が　{ \displaystyle \sqrt{m} } 以下であることが分かります.

 

　従って実際には自然数 { \displaystyle m } について

 

{ \displaystyle \frac{m}{2},\,\frac{m}{3},\,\dots,\,\frac{m}{\sqrt{m}-1} }

 

の { \displaystyle \sqrt{m}-2 }個とその床関数(ガウス記号)の結果が等しいかどうかをチェックすれば { \displaystyle m } が素数であるかどうかがわかるということです.

 

　予めfalseにしたフラグをつくり, 一つでも一致するならtrueに立てて, falseのままなら素数と判断できます.

 

 

 

フロー

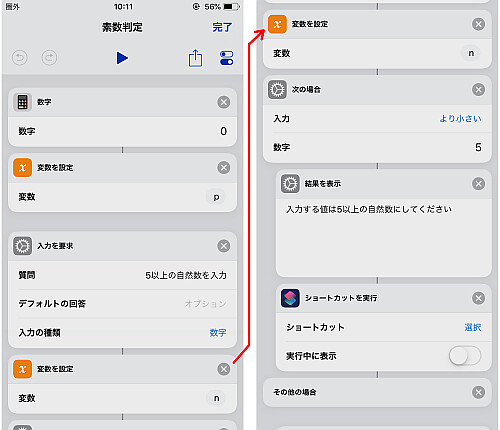
181103_17

　まずイニシャルとして素数判定用の変数 { \displaystyle p } に, デフォルト値として { \displaystyle 0 } (false) と置きます.

　またフローの都合上, 自明である { \displaystyle 2, 3, 4 } を弾くために「入力を要求」では { \displaystyle 5 } 以上の自然数を要求させます.

　そうでない場合は「次の場合」を利用して再び自分自身のショートカットを呼び出すことではじめからやり直します(「実行中に表示」はオフにするとスムーズに移行します).

 

 

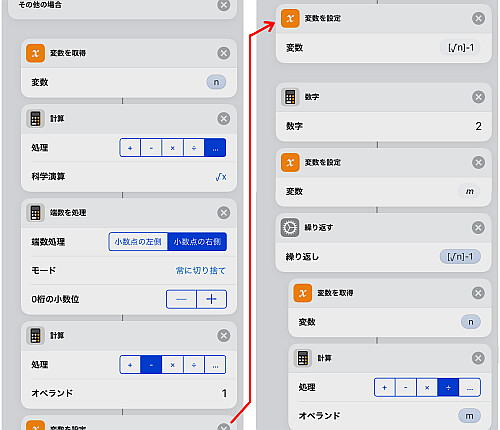
181103_18

　ここからがメインのフローです.

　改めて「入力を要求」で得た値 { \displaystyle n } を入力に代入し, 「計算」と「端数を処理」を組み合わせて { \displaystyle [\sqrt{n}]-1 } を計算します( { \displaystyle [\sqrt{n}]-2 } の誤りでしたが1つ余計に処理している以外結果に支障はありません).

　続いて先程あった

 

{ \displaystyle \frac{p}{2},\,\frac{p}{3},\,\dots,\,\frac{p}{p-1} }

 

の分母に合わせて繰り返しを行うため, 変数 { \displaystyle m } に { \displaystyle 2 } を代入します.

 

 

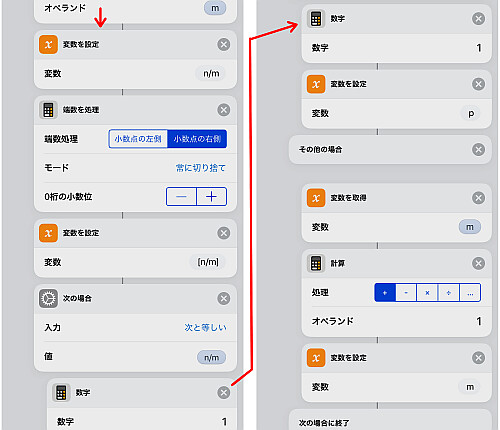
181103_19

　素数(候補)である { \displaystyle n } より { \displaystyle \frac{n}{m} } と { \displaystyle \left[ \frac{m}{n} \right] } を計算し, 等しければ 素数 { \displaystyle p } に { \displaystyle 1 }(true) を立て, 等しくなければ { \displaystyle p } は何もせず { \displaystyle m } に { \displaystyle 1 } を加えて次の繰り返しに戻ります.

 

 

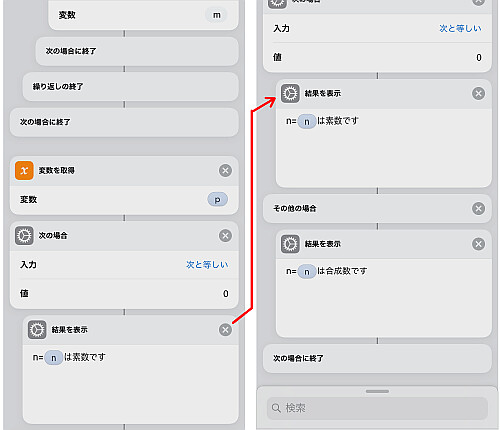
181103_20

　すべての繰り返しによって { \displaystyle p } が { \displaystyle 1 } になっていたら { \displaystyle n } は素数でない(=合成数), { \displaystyle 0 } のままなら素数ということになります.

 

 

実行

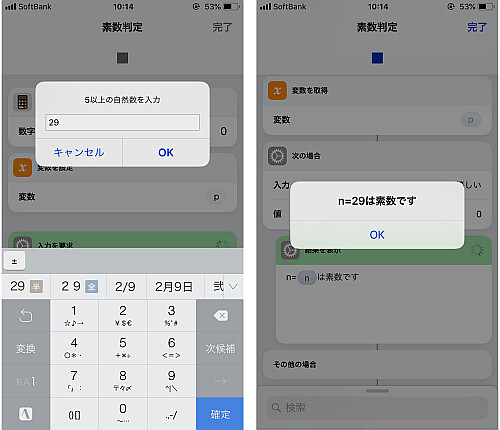
181103_21

　実行して結果が正しいことを確かめます.

 

 

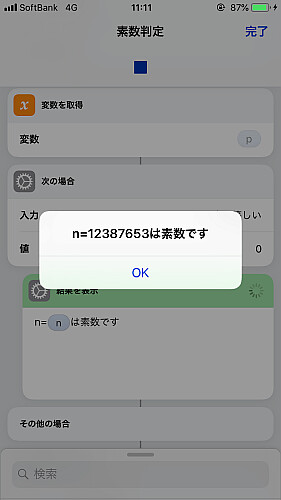
181103_22

　それなりに大きな数も結果を返してくれますが, 例えば画像の { \displaystyle 12387653 } の結果が変えるまで約5分34秒かかりました.

 

 

〆

　一つの結果を得るためにどうコーディングするかは一通りではありません.

　結果処理時間が早いか, 全体のコードの多寡ないし他人から見てわかりやすいか…等々の違いがありえます.

　当然コード(今回ならアクション)が少なく, かつ大きな値までサポートし, 処理時間も早いのが理想です.

　今回ははじめに理屈ありきなのでアイデア次第ではもっとエレガントなものを作る人がおられるでしょう.

 

 

URLスキームについてはこちら

[Search]iPhone URLスキーム -The theoryの戯言

iPhoneのURLスキームを検索して一覧表示できます. リクエストは内容に応じてお答えします.

 

 

thetheorier