もう一人のY君

iPhoneアプリのレビューやアップデートレビューなどを書いています. たまに数学の記事も書きます.

もう一人のY君　MENU 　MENU

【数学】外接・内接正多角形を用いた円周率近似

171105_00a

　今回は円に接する正多角形を用いた円周率の近似についてです.

 

 

スポンサーリンク

 

 

円周率の歴史

　円周率の存在は紀元前から知られており, この円に内接・外接する正多角形を用いた近似法も, 紀元前に活躍したアルキメデスと言われています.

 

　当時は小数以下2桁や3桁といった程度の精度でしたが, 比較的シンプルで計算も比較的用意であるため, より大きな正多角形を利用してより精度の高い円周率を求める手段の一つとして使われてきました.

 

　三角関数や級数といった概念が登場するまではこの手法が殆どで, これらを用いるようになった14世紀辺りに小数点以下10桁を超えます.

 

　現在はコンピュータの恩恵もあり, 三角関数や級数などを用いた式も高速で計算可能なのは言うまでもなく, 2016年の時点では20兆を超える桁まで判明しています.

 

 

正多角形を用いた近似

　今回は円に内接・外接する正多角形, 特に正 { \displaystyle 6\times 2^{n-1} } 角形を用いた円周率近似を考えてみます.

 

 

内接正6角形

　まず基本となる正六角形を考えます.

 

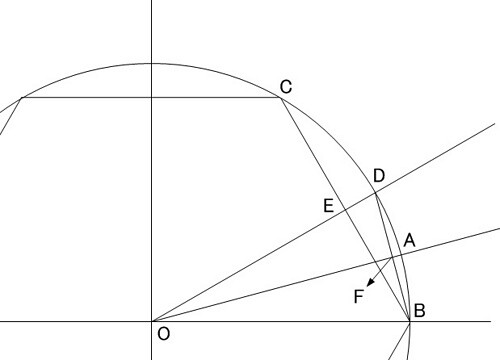
171105_01

　最初に内接六角形を考えましょう.

　円は単位円とし,単位円の中心を { \displaystyle O } , 点 { \displaystyle A,B,C,D } は単位円上の点で { \displaystyle B,C } は内接六角形の頂点, { \displaystyle D } は正六角形の次に考える正十二角形の頂点, 直線 { \displaystyle OD } と同 { \displaystyle BC } の交点を { \displaystyle E }, 同じく { \displaystyle OA } と { \displaystyle BD } の交点を { \displaystyle F } とします.

 

　このとき { \displaystyle \angle OEB } と { \displaystyle \angle OFB } は共に直角であることは明らかです.

 

　また円は単位円なので { \displaystyle OA } の長さは { \displaystyle 1 }, よって { \displaystyle BC } が単位円に内接する正六角形であることから { \displaystyle BE } の長さは { \displaystyle \frac{1}{2} } になります.

 

　単位円に内接する正六角形を用いた円周率「もどき」を求めることはもはやトリビアルでです, 従って最初に求めるべきは同じく正十二角形になります.

　正十二角形を用いた円周率「もどき」を求めるには例えば { \displaystyle BD } の長さが分かれば十分です.

　円周率は「円周÷直径」でしたから, 単位円に内接する正十二角形の円周率「もどき」は

 

{ \displaystyle \frac{12\times BD}{2} = 6\times BD }

 

で求まります.

　三平方の定理より { \displaystyle OB^2 = OE^2 + BE^2 } ですから, { \displaystyle OB=1 }, { \displaystyle BE = \frac{BC}{2} = \frac{1}{2} } より

 

{ \displaystyle 1^2 = OE^2 + \left(\frac{1}{2}\right)^2 }

{ \displaystyle \Rightarrow OE = \frac{\sqrt{3}}{2} }

 

でまず { \displaystyle OE } が求まります.

 

　{ \displaystyle DE = OD-OE } より { \displaystyle DE = 1-\frac{\sqrt{3}}{2} = \frac{2-\sqrt{3}}{2} } なので, { \displaystyle \bigtriangleup BDE } について三平方の定理を適用すると

 

{ \displaystyle BD^2 = BE^2 + DE^2 }

{ \displaystyle BD^2 = \left(\frac{1}{2}\right)^2 + \left(\frac{2-\sqrt{3}}{2}\right)^2 }

{ \displaystyle \Rightarrow BD = \sqrt{2-\sqrt{3}} }

 

を得ます.

　従って内接正12角形の円周「もどき」{ \displaystyle \pi_{in,2} } は

 

{ \displaystyle \pi_{in,2} = 6\times \left(\sqrt{2-\sqrt{3}}\right) }

 

となります.

 

　この時点で計算するとおよそ { \displaystyle 3.1058285412\dots } となり, 小数点以下1桁までしか合っていません.

 

 

内接正多角形の一般化

　上のやり方は次へと全く同じ方法で通用します.

　従って内接正 { \displaystyle 6\times 2^{n-1} } 角形として一般化してみましょう.

 

　正 { \displaystyle 6\times 2^{n-1} } 角形 { \displaystyle I_n } の一辺の長さを { \displaystyle a_n } とおきます.

　但し正6角形との都合を付けるために { \displaystyle a_0 = 1 } とします.

 

　このとき, { \displaystyle BC = a_n,\, BD = a_{n-1} } と置き換わるので, { \displaystyle \bigtriangleup OBE } に関して

 

{ \displaystyle OB^2 = OE^2 + BE^2} 

{ \displaystyle \Leftrightarrow 1^2 = OE^2 + \left(\frac{a_n}{2}\right)^2 }

{ \displaystyle \Rightarrow OE = \frac{\sqrt{4-a_n^2}}{2} }

 

となります.

　よって同じく { \displaystyle DE = OD-OE } から { \displaystyle DE = 1 - \frac{4-a_n^2}{2} } となり, { \displaystyle \bigtriangleup BDE } に関して三平方の定理を利用すると

 

{ \displaystyle BD^2 = BE^2 + DE^2 }

{ \displaystyle a_{n+1}^2 = \left(\frac{a_n}{2}\right)^2 + \left(\frac{1-\sqrt{4-a_n^2}}{2}\right)^2 }

{ \displaystyle \Rightarrow a_{n+1} = \sqrt{2-\sqrt{4-a_n^2}} }

 

となります.

 

　従って内接正 { \displaystyle 6\times 2^{n-1} } 角形の円周率「もどき」 { \displaystyle \pi_{in,n} } は,

 

{ \displaystyle \pi_{in,n}=6na_{n} } { \displaystyle = 6n\sqrt{2-\sqrt{4-a_{n-1}^2}},\, a_0=1 }

 

によって求まることになります.

 

 

外接正多角形の一般化

　外接正多角形についても考え方は同じです.

　なのでここではいきなり一般化からやってみましょう.

 

 

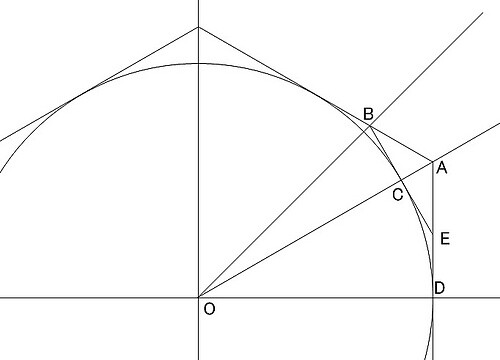
171105_02

　画像のように単位円とその外接する正多角形を考えます.

　以降は外接正 { \displaystyle 6\times 2^{n-1} } 角形と書くのが面倒なので { \displaystyle C_n } と書き表します.

　点 { \displaystyle C,D } は単位円上の点で, 点 { \displaystyle A } は { \displaystyle C_n } の頂点となります.

　直線 { \displaystyle AD } は { \displaystyle C_{n} } の辺の一部であり, 辺自体の長さを { \displaystyle b_n } とするならば, { \displaystyle AD = \frac{b_n}{2} } となります.

　{ \displaystyle BE } は { \displaystyle C_{n+1} } の一辺に相当し, これは { \displaystyle b_{n+1} } となります.

 

　今回は面積をもとに計算します, まず { \displaystyle \bigtriangleup OAD } について三平方の定理を適用すると

 

{ \displaystyle OA^2 = OD^2 + AD^2 }

{ \displaystyle \Leftrightarrow OA^2 = 1 + \left(\frac{b_n}{2}\right)^2 }

{ \displaystyle \Rightarrow OA = \frac{\sqrt{4+b_n^2}}{2} }

 

となるので

 

{ \displaystyle AC = OA - OC }

{ \displaystyle = \frac{\sqrt{4+b_n^2}}{2}-1 }

 

によって { \displaystyle AC } が求まります.

 

　面積について

 

{ \displaystyle \bigtriangleup ODC + \bigtriangleup OCE + \bigtriangleup ACE = \bigtriangleup ODA }

{ \displaystyle \Leftrightarrow 2\bigtriangleup OCE + \bigtriangleup ACE = \bigtriangleup ODA }

 

なのでこれにより

 

{ \displaystyle 2\cdot \frac{1}{2}\cdot \frac{b_{n+1}}{2} + \frac{2}{2}\cdot \left(\frac{\sqrt{4+b_n^2}}{2}-1\right)\cdot \frac{b_{n+1}}{2} = \frac{1}{2}\cdot 1\cdot\frac{b_n}{2} }

{ \displaystyle \Leftrightarrow b_{n+1} = \frac{2b_n}{2+\sqrt{4+b_n^2}} }

 

を得ます.

　なお今回の初期値は { \displaystyle b_0 = \frac{2}{\sqrt{3}} } となります.

 

　これを用いて円周率「もどき」を計算すると

 

{ \displaystyle \pi_{out,n}=6nb_n = \frac{12nb_{n-1}}{2+\sqrt{4+b_{n-1}^2}} } { \displaystyle ,\quad b_0 = \frac{2}{\sqrt{3}} }

 

となります.

 

 

実際計算してみる

　この2つの数列から, 円周率をある程度近似してみましょう.

　なお定義から

 

{ \displaystyle a_1\lt a_2\lt a_3\dots\lt\pi\lt\dots\lt b_3\lt b_2\lt b_1 }

 

であることがわかります.

 

 

正多角形  内接  外接 
6(n=1)  3.105828541230249  3.215390309173472 
12(n=2)  3.132628613281238  3.159659942097500 
24(n=3)  3.139350203046867  3.146086215131434 
48(n=4)  3.141031950890509  3.142714599645368 
96(n=5)  3.141452472285462  3.141873049979823 
192(n=6)  3.141557607911857  3.141662747056848 
384(n=7)  3.141583892148318  3.141610176604689 
768(n=8)  3.141590463228050  3.141597034321526 
1536(n=9)  3.141592105999271  3.141593748771352 
3072(n=10)  3.141592516692157  3.141592927385097 
6144(n=11)  3.141592619365383  3.141592722038613 
12288(n=12)  3.141592645033690  3.141592670701998 
24576(n=13)  3.141592651450767  3.141592657867844 
49152(n=14)  3.141592653055036  3.141592654659306 
98304(n=15)  3.141592653456104  3.141592653857171 

 

　この結果から分かる通り, n=15まで頑張っても小数以下9桁までしか一致しません.

　3.14を得るにしても外接でn=3, 内接でn=4までかかります.

 

 

〆

　一番有名であり, かつ四則演算と平方根のみで完結するため手計算でも出来ないことはないやり方ではあります.

 

　今回は正六角形からやりましたが正四角形からでも可能です.

 

thetheorier