もう一人のY君

iPhoneアプリのレビューやアップデートレビューなどを書いています. たまに数学の記事も書きます.

もう一人のY君　MENU 　MENU

(数学)判別式の意味

数学

 160323_00

　何となく…とか暗記で覚えてて応用に生かせない, 中途半端なイメージで覚えてるくらいなら, ちゃんとした意味(の一つ)で覚えておいた方が遥かにマシですよね.

　本来「知っているはず」なんですが意外とそうでもないのが現状のようです.

 

スポンサーリンク

 
[Contents]
 

 

判別式の定義

　言われなくてもそれは分かってるでしょうが書いておきますね.

　二次関数{ \displaystyle f(x) = ax^{2}+bx+c (a, b, cは実数, a\neq 0) }における以下の定数を判別式と言います.

{ \displaystyle D = b^{2}-4ac }

 

　二次方程式の実数解の個数を与える指標として利用されていますね.

　実際には二次関数どころか多項式について定義されますが, 多くの場合はそれを二次関数におけるそれと判断しますね.

 

 

何故これが実数解の個数を与えるのか

　判別式の計算式はもちろん, その結果が実数解の個数の指標であることは分かっていても, 「何故そうなのか」に答えられる学生が(一部でしょうが)いるようです.

　判別式を学んでる頃にはその理由に答えられるはずです.

　今回は2つの視点から見てみることにします. 

 

　以降, 二次関数と言えば{ \displaystyle f(x) = ax^{2}+bx+c (a, b, cは実数, a\neq 0) }, 二次方程式と言えば{ \displaystyle f(x) = 0 }を意味するものとします.

 

 

(1)解の公式から理解する

　二次方程式の解の公式を見ればもう一目瞭然です, 一番簡単かもしれませんね.

　平方完成から比較的簡単に導かれます, すなわち

{ \displaystyle ax^{2}+bx+c = 0 }

{ \displaystyle \Leftrightarrow ax^{2}+bx = -c }

{ \displaystyle \Leftrightarrow ax^{2}+bx+\frac{b^{2}}{4a}-\frac{b^{2}}{4a} = -c }

{ \displaystyle \Leftrightarrow a\Bigl(x^{2}+\frac{b}{a}x+\frac{b^{2}}{4a^{2}}\Bigr)=\frac{b^{2}}{4a}-c }

{ \displaystyle \Leftrightarrow a\Bigl(x+\frac{b}{2a}\Bigr)^{2} = \frac{b^{2}-4ac}{4a} }

{ \displaystyle \Leftrightarrow \Bigl(x+\frac{b}{2a}\Bigr)^{2} = \frac{b^{2}-4ac}{4a^{2}} }

{ \displaystyle \Leftrightarrow x+\frac{b}{2a} = \pm\frac{\sqrt{b^{2}-4ac}}{2a} }

{ \displaystyle \Leftrightarrow x = -\frac{b}{2a}\pm\frac{\sqrt{b^{2}-4ac}}{2a} }

{ \displaystyle \Leftrightarrow x = \frac{-b\pm\sqrt{b^{2}-4ac}}{2a} }　…(※)

 

ですね.

　注目すべきは平方根の中身である{ \displaystyle b^{2}-4ac }の部分です.

　ここで{ \displaystyle D := b^{2}-4ac }と定めましょう.

 

D>0のとき

　このとき { \displaystyle \sqrt{D} } の値は実数です.

　従って(※)は実数の値2つということですね.

　つまり方程式{ \displaystyle f(x) = 0 }の実数解は2つです.

 

D=0のとき

　このとき解は { \displaystyle x = -\frac{b}{2a} } ただ一つです.

　実数の四則演算はまた実数ですから, このとき方程式{ \displaystyle f(x) = 0 }は実数解をただ一つ持ちます.

 

D<0のとき

　このとき値{ \displaystyle \sqrt{b^{2}-4ac} }は順虚数ですから, 解(※)の値は異なる二つの複素数と言えます.

  

　このように, 解の公式にある平方根の部分を評価することで, 方程式の実数解の個数を求めることができます.

 

　以上から

{ \displaystyle D＞0 } 実数解2個
{ \displaystyle D=0 } 実数解1個(重解)
{ \displaystyle D＜0 } 実数解なし

が分かります.

 

 

グラフを使う

thetheorier.hatenablog.com

　以前のエントリで, 任意の関数は一つのグラフを定義すること, そして同時にそのグラフと方程式の実数解に関わりがあることを説明しました.

　これもある意味では当たり前ですが, ごく自然に考えられるためか学校ではあまり深く立ち入りません.

　その話は上記エントリに譲るとして, この概念を利用して, 二次関数によるグラフにおいて, 判別式はどんな存在なのか…を考え, それによって判別式の意味, イメージを掴んでみることにします.

 

 

平方完成

　二次関数のグラフと言えば平方完成ですね.

　これによって二次関数によるグラフの頂点の座標が分かります.

　二次関数{ \displaystyle f(x) = ax^{2}+bx+c }が{ \displaystyle f(x) = a(x-p)^{2}+q }という形になるとき, この二次関数の頂点の座標は

{ \displaystyle (p, q) }

になるというやつです.

　上で似たようなことをやっているので拝借すると, 

{ \displaystyle f(x) = ax^{2}+bx+c }

{ \displaystyle = a\Bigl(x+\frac{b}{2a}\Bigr)^{2}-\frac{b^{2}-4ac}{4a} }

…となることから, 頂点の座標は

{ \displaystyle \Bigl(-\frac{b}{2a}, -\frac{D}{4a}\Bigr) }

となることが分かります( { \displaystyle D=b^{2}-4ac } を予め代入してあります).

 

　ここから分かるのは, (二次関数の)判別式とは頂点のY座標の一部であるということです.

　分母にあるのは数4とグラフの凸性の向きを決めるaだけ…

 

　二次関数のグラフは, { \displaystyle x^{2} }の係数の正負によって上下どちらに凸か, そして上記の頂点の座標, この2つである程度特徴づけることができます.

　今回は { \displaystyle a＞0 } に絞って考えてみましょう.

 

 

中間値の定理

　証明はここではしませんが以下で使用しているので紹介しておきます.

　当たり前に見えるんですがちょっと証明はめんどくさいのです…

[中間値の定理]
　実数直線{ \displaystyle \mathcal{R} }の閉区間 { \displaystyle I= } [ { \displaystyle a, b } ]上で連続な実数値関数 { \displaystyle f(x) } が { \displaystyle f(a)＜f(b) } を満たすとき, 閉区間 [ { \displaystyle f(a), f(b) } ] 上の任意の点 { \displaystyle r } に対して, { \displaystyle r=f(c) } を満たす点 { \displaystyle c\in I } が存在する.

 

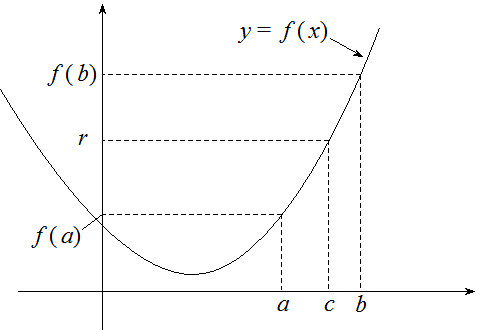
　今回は二次関数, 方程式, 判別式…ということで, これをもう少し具体的にして,

　実数直線{ \displaystyle \mathcal{R} }の閉区間 [ { \displaystyle a, b } ]上の二次関数 { \displaystyle f(x) } が { \displaystyle f(a)\leq 0＜f(b) } , あるいは { \displaystyle f(a)＜0\leq f(b) }の一方を満たすとき, { \displaystyle f(c)=0 } を満たす点 { \displaystyle c\in I } が存在する.

として差し支えないでしょう.

　つまり方程式の解となる座標 { \displaystyle (x_{0}, 0) } と, その左右を評価すれば十分です.

 

 

{ \displaystyle a＞0, -\frac{D}{4a}＜0 } のとき

　このとき, うまく { \displaystyle m, n\in\mathcal{R} } を選ぶことで, 閉区間 [ { \displaystyle m, -\frac{b}{2a} } ], [ { \displaystyle -\frac{b}{2a}, n } ] に対してそれぞれ { \displaystyle f(m)＜f(-\frac{b}{2a}), f(-\frac{b}{2a})＜f(n) } であり, かつそれぞれ { \displaystyle f(x_{1})=0, f(x_{2})=0 } となるような実数 { \displaystyle x_{1}, x_{2} } が存在します.

　これはつまり { \displaystyle x_{1}, x_{2} } が方程式 { \displaystyle f(x)=0 } の二つの実数解であることを意味しています.

　中間値定理など面倒な理屈を使ってますが図によるイメージは掴めるでしょう.

 

　このとき

{ \displaystyle -\frac{D}{4a}＜0 }

{ \displaystyle \Leftrightarrow D＞0 }

であることも分かります.

 

{ \displaystyle a＞0, -\frac{D}{4a}=0 } のとき

　このとき, 例えば { \displaystyle m＞-\frac{b}{2a} } を満たす任意の実数 { \displaystyle m } による閉区間 [ { \displaystyle -\frac{b}{2a}, m } ] を考えれば { \displaystyle f(\frac{b}{2a}) = -\frac{D}{4a} = 0 } なので, もはや中間値定理を考えるまでもなく { \displaystyle x = -\frac{b}{2a} } のみを解とします.

　重解というやつですね.

　このとき { \displaystyle D = 0 } であることも { \displaystyle a＞0 } から明白です.

 

{ \displaystyle a＞0, -\frac{D}{4a}＞0 } のとき

　このとき, 任意の { \displaystyle m\in\mathcal{R} } に対して { \displaystyle f(m)＞0 } ですから, どのように閉区間を取っても { \displaystyle f(a)\leq 0＜f(b) }, 及び { \displaystyle f(a)＜0\leq f(b) } を満たす { \displaystyle a, b } は取れません.

　従って画像からも明らかですが, { \displaystyle f(c)=0 } なる { \displaystyle c }, つまり方程式 { \displaystyle f(x)=0 } の実数解は存在ません.

　このとき

{ \displaystyle -\frac{D}{4a}＞0 }

{ \displaystyle \Leftrightarrow -D＞0 }

{ \displaystyle \Leftrightarrow D＜0 }

となります.

 

　以上から

{ \displaystyle D＞0 } 実数解2個
{ \displaystyle D=0 } 実数解1個(重解)
{ \displaystyle D＜0 } 実数解なし

が分かります.

 

 

〆

　意味さえ分かれば判別式そのものも, その応用もそつなくこなすことができるでしょう.

　なお後者は応用でも使えます.

 

thetheorier.hatenablog.com

　以前の記事もどうぞ.

　ホントは今回のを先に書くべきだった…

 

 

 

 

thetheorier