もう一人のY君

iPhoneアプリのレビューやアップデートレビューなどを書いています. たまに数学の記事も書きます.

もう一人のY君　MENU 　MENU

(数学)同値関係、商集合

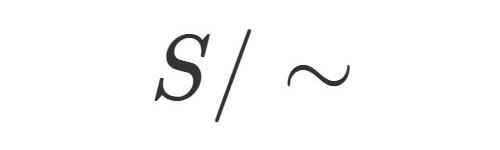
161106_01

　タイトルにある2つの文字, 多くの方は聞いたことはないと思います.

　しかし実際には日常で当たり前に使ったり考えたりしている概念になります.

　そして数学においても非常に重要で便利な概念になります.

 

[Contents]
 

 

商を取る, 同値である

　例えば「曜日」を考えてみましょう.

　ある月の1日と8日は明らかに「違う日」です.

　しかしこの2つは「同じ曜日」ですね.

 

　このように, 見方によって違うものを, それを通して「同じものとみなす」のがここで言う商や同値の考え方です.

 

　折角なのでそのたびにこの「曜日」で具体的に比較してみましょう.

　しかしこれは同時に「合同式」で評価していることも直ぐに分かることでしょう.

 

 

同値関係

　ではまず同値関係から見ていきましょう.

 

[定義：同値関係]

　集合 { \displaystyle S } と, { \displaystyle S } の任意の元による条件 { \displaystyle \sim } を { \displaystyle S } 上の「関係」と言います.

　例えば 「{ \displaystyle a-b } が{ \displaystyle 7 }の倍数であるとき { \displaystyle a\sim b }」とすれば, これは { \displaystyle a-b } が7の倍数という条件において { \displaystyle a, b } は同じであると見なし, これを { \displaystyle a=b } などを書く代わりに { \displaystyle a\sim b } と書くわけです.

 

　このとき, { \displaystyle \sim } が { \displaystyle S } 上の同値関係であるとは, 以下の3つを満たすこととします.

 

　{ \displaystyle S } の任意の元 { \displaystyle a,b,c, } について,

  1. { \displaystyle a\sim a }.
  2. { \displaystyle a\sim b } ならば { \displaystyle b\sim a }.
  3. { \displaystyle a\sim b } かつ { \displaystyle b\sim c } ならば, { \displaystyle a\sim c }.

(曜日を使った例)

　ある月の2つの日付 { \displaystyle a, b } の差が7の倍数であるとき { \displaystyle a\sim b } とすると, 例えば

 

{ \displaystyle 1-8=-7=7\times (-1) \\ 2-16=-14=7\times (-2) \\ 3-24=-21=7\times (-3) \\ \dots}

 

なので, 1日と8日, 2日と16日, 3日と24日, ... は各々関係 { \displaystyle \sim } において同じです.

 

　ここで, 流儀やカテゴリ次第では関係を以下のように表すこともあります.

 

  • 関係 { \displaystyle R } とし, 関係が成り立つことを { \displaystyle aRb } と書く
  • 関係 { \displaystyle R } を { \displaystyle S } の直積 { \displaystyle S\times S } の部分集合と定める { \displaystyle \bigl( (a,b)\in R \bigr) }

 

　この3種類のどれを使用するかはその講師・参考書次第です.

　このエントリでは最初の { \displaystyle \sim } で統一します.

 

　また定義から気付く方もいるでしょうが, この同値関係は図形の相似や合同とも繋がっています.

 

 

スポンサーリンク

 

同値類

　同値関係とは { \displaystyle S } の任意の元を関係 { \displaystyle \sim } による新たな「等式関係らしいもの」を生み出します.

　簡単に言えば「同じ性質のもの」です.

　その同じ性質のものだけをかき集めた集合を同値類と呼びます.

 

[定義：同値類]

　集合 { \displaystyle S } と { \displaystyle S } の任意の元 { \displaystyle a }, 更にその上の同値関係 { \displaystyle \sim } について, 次の類は同値類と呼ばれます.

 

{ \displaystyle [a] := \{ b\in S | a\sim b \} }

(曜日を使った例)

　ある月の4日が月曜日だった場合, 

 

{ \displaystyle [4]=\{ b\in Mon | 4\sim b \} \\ =\{ 4, 11, 18, 25 \} }

 

とは「月曜日である日付を集めた集合」と言えます.

※{ \displaystyle Mon } はその月の日付の集合(数対象)です, 余り深く考えないようにしてください

 

　定義から, 以下の性質が成り立つことは明らかです.

 

  • { \displaystyle a\sim b } のとき, { \displaystyle [a]=[b] }.
  • { \displaystyle a\not\sim b } のとき, { \displaystyle [a]\cap[b]=\emptyset }
  • 任意の { \displaystyle a\in S } が, 異なる複数の同値類に属することはない

 

　以上より, { \displaystyle S } の任意の元を, いくつかの同値類に重複することなく, また互いの同値類が共通する元を持たないように「カテゴリ分け」することができます.

　これを「類別」と言います.

 

　曜日で言えば, ある月の日付を7つの曜日による同値類にカテゴリ分けすることができるという意味です.

 

　同値関係が合同式であるとき, その同値類は特別に「剰余類」と呼ばれます.

 

 

商集合

　以上の同値関係, そして同値類を用いて, 以下のように商集合が定められます.

 

[定義：商集合]

　集合 { \displaystyle S } とその上に定められた同値関係 { \displaystyle \sim } について, 以下のように商集合を定める.

 

{ \displaystyle S/\sim := \{ [a]\,|\, a\in S \} }

(曜日を使った例)

　曜日は7種類ですから, 先程の同値類の性質も踏まえると例えば

 

{ \displaystyle Mon/\sim\, =\,\{[1], [2], [3], [4], [5], [6], [7]\} } 

 

と言えます, 当然

 

{ \displaystyle \{[2], [3], [4], [5], [6], [7], [8]\} } 

 

などでも同じです.

 

 

商環・商体

　商集合 { \displaystyle S/\sim } は, 各々の { \displaystyle S } や { \displaystyle \sim } に応じて自然な演算を与えることで環や体を成します.

　それらの環, 体は各々商環, 商体と呼ばれます. 

　当然合同式の場合は例えば剰余環と呼ぶことになります.

 

　この同値関係から商環に至る流れによって, 例えば自然数から整数, 整数から有理数…といった代数系の構築を行うことができます.

 

　例えば, 自然数から整数を構築するには, 同値関係として

 

{ \displaystyle \forall a, b, c, d\in\mathbb{N} \\ a+d = b+c\,\Rightarrow (a, b)\sim (c, d) }

 

 , また整数から有理数を構築するには,

 

{ \displaystyle \forall a, b, c, d\in\mathbb{R}\,,\quad b, d\neq 0 \\ ad = bc\,\Rightarrow (a, b)\sim (c, d) }

 

とすれば良いです.

 

　実際これで良いか, 確かめてみましょう.

 

 

thetheorier