もう一人のY君

iPhoneアプリのレビューやアップデートレビューなどを書いています. たまに数学の記事も書きます.

もう一人のY君　MENU 　MENU

(数学)オイラーの定理、フェルマーの定理

数学

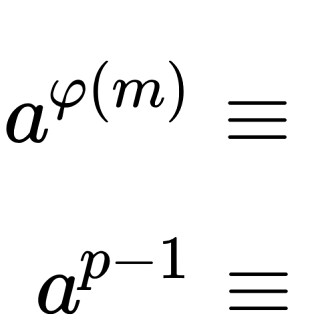
 160201_10

　最終定理のアレじゃなく, 合同式です.

 

[Contents]
 

 

thetheorier.hatenablog.com

　合同式の定義はこちらから.

 

 

剰余類・既約剰余類

　まずは剰余類と既約剰余類の話からです.

　合同式を扱っていれば分かる通り, 法 { \displaystyle m } に関して, いかなる数も

 { \displaystyle 0, 1, 2, ..., m-1 }

のいづれかただ一つと合同であり, また連続した数はこの { \displaystyle m } 個の数が周期的に並びます.

　言ってみればこの { \displaystyle m } 個の数が任意の整数を代表しているわけです, このとき集合1

{ \displaystyle \{ 0, 1, 2, ..., m-1\} }

を法 { \displaystyle m } の剰余系と言います.

　このとき剰余系の元を「代表」などと言います.

 

　当然, 例えば { \displaystyle 0 } は 法 { \displaystyle m } に関して { \displaystyle m } と合同ですから, 上の剰余系は

{ \displaystyle 1, 2, ..., m }

と書き変えても同じものと見なすことができます, つまり代表となる元は, 法 { \displaystyle m } に関して同じであればそれに差し替えても剰余系になります.

　が, 一般的には 

{ \displaystyle \{ 0, 1, 2, ..., m-1\} }

を使うことが多いです.

 

 

既約剰余系

　法 { \displaystyle m } に関して, { \displaystyle m } と互いに素な元のみによって組まれた系を, 法 { \displaystyle m } の既約剰余系と言います.

　例えば { \displaystyle m=8 } のとき, { \displaystyle 8 } 未満の非負整数で { \displaystyle m=8 } と互いに素な数は { \displaystyle 1, 3, 5 } になるので, 法 { \displaystyle m=8 } の既約剰余系は例えば

{ \displaystyle \{1, 3, 5\} }

となります.

　また法 { \displaystyle m } が素数 { \displaystyle p } であるとき, { \displaystyle 1, 2, ..., p-1 } のいずれも { \displaystyle p } と互いに素ですから, 法 { \displaystyle p } の既約剰余系は

{ \displaystyle \{1, 2, ..., p-1\} }

となり, 剰余系と同一になります.

 

 

オイラーの定理

　オイラーの定理もフェルマーの定理も, 複数の証明が存在しますが, 今回は上記の既約剰余系を用いた方法で, オイラーの定理を証明することから行います.

[オイラーの定理]

　{ \displaystyle \gcd(a, m)=1 } を満たす整数 { \displaystyle a } と正整数 { \displaystyle m }について,

{ \displaystyle a^{\varphi(m)}\equiv 1 \pmod m }

 

オイラーの定理の証明

　{ \displaystyle \gcd(a, m)=1 } のとき, 法 { \displaystyle m } の剰余系

{ \displaystyle x_{1}, x_{2},\dots, x_{m} }

を与えたとき, 各々に { \displaystyle a } をかけ合わせたもの

{ \displaystyle ax_{1}, ax_{2},\dots, ax_{m} }

による系はやはり法 { \displaystyle m } の剰余系になります.

　まずはこれを示しましょう.

 

　仮に

{ \displaystyle ax_{h}\equiv ax_{k}\pmod m }

と仮定すると, 合同式の定義からこれは { \displaystyle a(x_{h}-a_{k}) } が { \displaystyle m } で割り切れるということです.

　{ \displaystyle a } は { \displaystyle \gcd(a, m)=1 } より { \displaystyle m } と互いに素ですから, { \displaystyle a_{h}-a_{k} } が { \displaystyle m } で割り切れることになります, よって

{ \displaystyle a_{h}\equiv a_{h}\pmod m }

です.

　{ \displaystyle h, k } は剰余系の理屈から { \displaystyle 1, 2, \dots, m } のいづれかですから, これを満足するのは { \displaystyle h = k } の場合に限られます.

　従って { \displaystyle ax_{1}, ax_{2},\dots, ax_{m} } もまた剰余系になります.

 

　これは既約剰余系についても当然成り立ちます, 従って法 { \displaystyle m } に関する { \displaystyle \varphi(m) } 個の既約剰余系

{ \displaystyle x_{1}, x_{2},\dots, x_{\varphi(m)} }

を与えたとき,

{ \displaystyle ax_{1}, ax_{2},\dots, ax_{\varphi(m)} }

もまた法 { \displaystyle m } の既約剰余系となることが分かります.

　この2つの既約剰余系は個数が等しく, 一方のある代表元が他方の代表元一つと合同になりますから,

{ \displaystyle ax_{1}\times ax_{2}\times\dots\times ax_{\varphi(m)}\equiv x_{1}\times x_{2}\times\dots\times x_{\varphi(m)}\pmod m }

, つまり

{ \displaystyle a^{\varphi(m)}x_{1}x_{2}\dots x_{\varphi(m)}\equiv x_{1}x_{2}\dots x_{\varphi(m)}\pmod m }

となります.

　{ \displaystyle \varphi(m) } はオイラーの関数, つまり { \displaystyle m } と互いな自然数の個数でしたね？

　また { \displaystyle x_{i}　(i=1, 2,\dots, m) } は既約剰余系の理屈からいずれも { \displaystyle m } と互いに素, つまり { \displaystyle \gcd(x_{1}x_{2}\dots x_{\varphi(m)}, m) = 1 } ですから, 上の合同式を, 法を保ったまま割ることができます, 従って

{ \displaystyle a^{\varphi(m)}\equiv 1\pmod m }

が得られます. { \displaystyle \square }

 

 

フェルマーの定理

　続いてフェルマーの定理です.

　フェルマーの最終定理が有名であるため, これと区別して「フェルマーの小定理」とも呼ばれます.

　今回は先にオイラーの定理を証明したので系(Corollary)に相当します.

[フェルマーの(小)定理]

　素数 { \displaystyle p } と, { \displaystyle p } で割り切れない整数 { \displaystyle a } について,

{ \displaystyle a^{p-1}\equiv 1\pmod p }

 

フェルマーの定理の証明

　{ \displaystyle a } が { \displaystyle p } で割り切れないことから

{ \displaystyle \gcd(a, p)=1 }

, また既約剰余系の話からも明らかですが, 素数 { \displaystyle p } について

{ \displaystyle \varphi(p)=p-1 }

が成り立つことから明らかに成り立ちます. { \displaystyle \square }

 

 

〆

　余裕があればフェルマーの定理の別証明も書きたいところです.

 

 

  1. 正しくは集合でなく類(class)と言うべきですが.

 

 

thetheorier