もう一人のY君

主にiPhoneのショートカットアプリのレシピやTipsなどを書いています. たまに数学の記事も書きます.

もう一人のY君　MENU 　MENU

(数学)数式とは, 多項式とは, 関数とは

数学

Last modified：2017.04.20

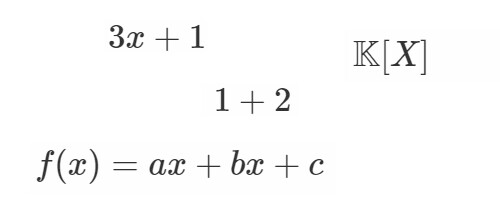
160607_00

　数学の世界では色んな文字列を扱いますが, それに色んな条件を加えて更に別の呼び名になったりします.

　その時は覚えていても増えていくうちにどれが何の意味か忘れてしまうものです, 簡単にまとめてみたいと思います.

 

[Contents]

 

 

 

文字列

　ここで言う文字列とは, 我々が普通に扱っている数記号やアルファベット, ギリシャ文字などを並べたものを指しますが, 当然ながら指数や対数などの記号表記も含んでいます.

　この時点ではただ文字を並べただけであり, 変数とか係数とかそういう概念はありません.

 

 

数式

　文字列のうち, 数記号やアルファベットなどの文字記号を, 結合算法(四則演算や指数, 対数など)など数学のルールに従って結合したものを数式と言います.

　例えば

{ \displaystyle 1+2 }

{ \displaystyle 3x+4y }

{ \displaystyle \sqrt{\sum_{n=1}^{5}\log_{6}(n\sin(5-n)\theta)} }

などがそうです.

　ここで { \displaystyle x } や { \displaystyle y }, { \displaystyle \theta } などを変数や不定元と言いたいところですが, 数式と呼んでいる時点では必ずしもそのように呼び分ける必要はありません(必要があれば構いません).

 

 

多項式

　多項式とは,

  • 定数
  • 変数(または不定元)

と呼ばれる数や文字, 或いはこれらによる線形和, つまり足し算と掛け算の組み合わせによって得た文字列のことです.

　例えば

{ \displaystyle 3 }

{ \displaystyle 3x+4y }

{ \displaystyle x^{3}+2y+5 }

は多項式です( { \displaystyle 3} のような単項式(後述)については別定義もあり)が,

{ \displaystyle \sqrt{\sum_{n=1}^{5}\log_{6}(n\sin(5-n)\theta)} }

は平方根や三角関数, 対数があるので多項式ではありません.

 

　多項式は例えば一般に,　係数を成す定数の集合 { \displaystyle K } と不定元 { \displaystyle X } を用いて

{ \displaystyle a_{n}X^{n}+a_{n-1}X^{n-1}+...+a_{1}X+a_{0} }

{ \displaystyle (a_{i}\in K,　i = 1, 2, ..., n) }

　と書き表され, 各々の { \displaystyle a_{i}X^{i} } を項, また { \displaystyle a_{0} } の部分を特別に定数項と呼びます.

　ここで上の形の多項式をすべて集めた集合を { \displaystyle K[X] } と書き表します, つまり

{ \displaystyle a_{n}X^{n}+a_{n-1}X^{n-1}+...+a_{1}X+a_{0}\in K[X] }

ですね.

　当然不定元が増えれば 例えば { \displaystyle K[X, Y] } ... となるわけです.

 

 

単項式

　{ \displaystyle 3x^2 } や { \displaystyle y } のように, 多項式で言うところの各々の項のみであるものを特別に単項式と言います.

　(係)数のみの場合は次数(後述) { \displaystyle 0 } と見なすことで単項式とするのが一般的です.

 

 

(多項式の)次数

　次数という言葉は, カテゴリによって意味が違ってきます.

　多項式の場合, { \displaystyle a_{n}X^{n}+a_{n-1}X^{n-1}+...+a_{1}X+a_{0} } { \displaystyle (a_n\neq 0) } の任意の多項式における次数とは { \displaystyle n } のことを指し, { \displaystyle \text{deg}(f) } などと表記します.

　つまり例えば { \displaystyle g(X)=2x^3-4X+3 } なら { \displaystyle \text{deg}(g)=3 } になります.

　

 

整式

　多項式の定義は前述の通りですが, 一般的に「多項式」として議論する際に実際に扱うのは次数が2以上であることが多いです.

　そのため多項式…と言ったら単項式を除くケースがあり, その場合は多項式と単項式を含めたものを整式と呼びます.

　参考書によってこの辺は違うので各々に従いましょう.

 

 

関数

　関数とは, 数式 { \displaystyle f } と二つの集合 { \displaystyle A, B } との間に然るべき定義がなされたものを言います.

thetheorier.hatenablog.com

　詳しい解説は上の通りですが改めて定義だけここにも書いておきます.

 

　集合 { \displaystyle A, B } の順序対 { \displaystyle \langle a, b\rangle } が次を満たすとき, { \displaystyle f } は { \displaystyle A } から { \displaystyle B } への関数と呼びます.

  1. { \displaystyle f } の元はすべて { \displaystyle \langle a, b\rangle } の形であり, かつ { \displaystyle a\in A }, { \displaystyle b\in B } を満たす
  2. { \displaystyle \langle a, b\rangle\in f } かつ { \displaystyle \langle a, c\rangle\in f } ならば, { \displaystyle a=c }
  3. { \displaystyle A } の任意の元 { \displaystyle a } について, { \displaystyle \langle a, b\rangle\in f } となるような { \displaystyle B } の元 { \displaystyle b } が存在する

　そしてこのとき, { \displaystyle b = f(a) } と書き表します.

 

　このとき { \displaystyle A } を定義域と呼び, { \displaystyle B } はその時の扱いによって終域, 或いは値域と呼びますが, いづれにしろ重要なのは, その数式を関数と呼ぶ以上, 定義域と終域(値域)に相当する2つの集合が存在していることが大前提となることは間違いありません.

　数式だけでは関数になれないのです.

 

　また定義から多項式は数式の一部です, 従って定義を満たすような2つの集合を用意すればその多項式は関数となりえるわけです.

　例えば一般な二次関数とは, 次数が2の多項式と, 然るべき定義域, 終域によるものというわけです.

　強いて言うなら, 関数とは次の三つ組であるとも言えます.

{ \displaystyle (f(x), A, B) }

　我々が普段関数と言っている時は, これを省略して { \displaystyle f(x) } としてしまっているだけというわけです.

 

 

数式と関数の違い

　この二つの違いは上にある通り定義域や終域を考えるかどうかですが, より分かりやすく言えば「不定元(変数)に値を代入するかどうか」の話でもあります.

 

　数式は, 等式や不等式などを用いて変形することはあれど, その時点では不定元に値を代入することはしません.

　一方関数はその不定元に値を代入して得られる結果を評価することを目的の一つとします.

 

　一般にはひっくるめて扱うのでその線引きに意味を感じる事が薄いと思いますけどね.

 

 

多項式関数

　上のややこしい区別に意味を感じうるのはまさにこれだと思います(個人的に).

　多項式

{ \displaystyle a_{n}X^{n}+a_{n-1}X^{n-1}+...+a_{1}X+a_{0} \in K[X] }

{ \displaystyle (a_{i}\in K,　i = 1, 2, ..., n) }

は, 不定元に何らかの数を代入することができます.

　代入したらその結果は { \displaystyle K } の元, つまり何らかの値になります.

　不定元 { \displaystyle X } に代入した数によって値 { \displaystyle f(X) } が決まりますから, これも関数になるわけです.

 

　従って, 関数とは数式 { \displaystyle f } と2つの集合 { \displaystyle A, B } によるものでしたが, 今回は多項式 { \displaystyle f(X) } と集合 { \displaystyle K } による関数, つまり

{ \displaystyle f:K\to K }

と見なすことができます.

　このとき { \displaystyle f \equiv (f, K) } を多項式関数と言います.

 

　多項式関数 { \displaystyle f } の次数 { \displaystyle \deg (f) } が { \displaystyle n } であるとき, 多項式 { \displaystyle f } の定める多項式関数を { \displaystyle n }次関数と言います.

　つまり我々がよく扱っている2次関数 { \displaystyle ax^{2}+bx+c } は, 関数の中でも { \displaystyle K = \mathbb{R} } である2次の多項式関数 { \displaystyle \mathbb{R}[x] } ということになります.

 

　多項式は数式の特別な場合でしたから, 多項式関数は関数の特別な場合とも解釈できます.

 

 

〆

　大まかに言ってしまえば, 数式は式そのもの, 関数はそれに定義域と終域を成す集合の組のことです.

 

　何となく区別がついたでしょうか？

 

 

thetheorier