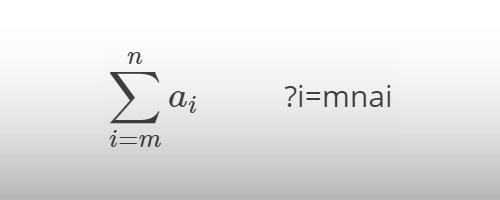
質問サイトなどを利用していると, 各々のフォームでは例えば や
といった書き方は出来ません.
特殊記号を使用すれば一部は解決するように思えますが, 閲覧者の環境によっては文字化けしてしまうため, あまりオススメ出来ません.
従ってどんな環境でも閲覧できる記号, 記法で代用する手法を取ることが大半です.
先に行ってしまえばその多くがC言語をはじめとするプログラミング言語の言語体系をそのまま流用しています.
気を付けてほしいのは, これらは飽くまでもこういった場での代用であり, 実際に紙に書いたり公に提出する際に代用記号, 記法で行うのは誤りであるということです.
数学の世界に限らず, 記号, 記法には一定の慣例が存在します.
個々人が好き勝手に決めてそのように使うこと自体は自由ですが, それを読む立場からすれば一々分かるように「翻訳してもらう」手間が必要になります.
各々の記号や記法が生まれた時代によっては, 現在ほどの素早いコミュニケーションが無かったため, 同じモノであっても各々の発案者, 地域によって様々な使い方をしていましたが, 一部を除いてある程度慣例化されています.
これは上記の通り, そのように書けば説明することなく万人に理解してもらえるようにするためですから, その線引きはハッキリさせておきましょう.
代用例
僕が把握している範囲で…ですが以下に書きならべておきます, 毎度「○○ってどういう意味ですか?」と聞く手間が少しでも省ければ幸いです.
| 記号・式 | 代用例 |
|---|---|
| a/b | |
| a/b | |
| a^b | |
| pow(a,b) | |
| log[a]b | |
| a[n] | |
| a_n | |
| lim[x→∞]f(x) | |
| Σ[i=m…n]a[i] | |
| ∫[m…n]f(x)dx | |
| ∪[n=1…m]U[n] | |
| x^(m/n) | |
| ↑a | |
| φ | |
| 1101(2) | |
| C(n, m) | |
| A^c | |
| a\∈A |
代用表記による弊害
代用表記は言ってみれば急場しのぎのため, 通常とは異なる配慮をしないと相手にキチンと伝わらない場合があります.
例えば以下の場合が考えられます.
- a/b+c
とも
とも判断できます.
従って見た目が宜しくないですが
a/(b+c)
(a/b)+c
などと括弧を付けてはっきり区別します.
- √a+b
これもやはり とも
とも判断できます, よって
√(a+b)
(√a)+b
と, どちらなのかハッキリ分かるようにします.
他にも例えば a^b+c や log[a]b+c のように, 相手に誤解を与えかねない表現はたくさんあります, 慣れるか, 無理なら手書きの画像にするかしましょう.
また, 場合によってはその記法を予め断っておく必要もあるかもしれません, ここに書いてあるものが必ずしも一般的とは断言しないことをここで断っておきます.
上で紹介したものも然りです.
〆
気を付けるのはこのくらいだと思いますが, まだあったら追加します.
