もう一人のY君

iPhoneアプリのレビューやアップデートレビューなどを書いています. たまに数学の記事も書きます.

もう一人のY君　MENU 　MENU

【数学】ピンポイント問題1

数学 数学-問題

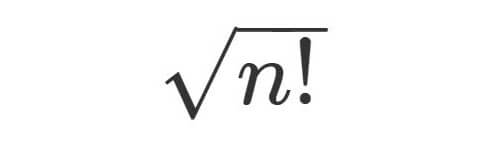
161006_05

　たまにはですね, 面白い問題があれば(解けたかどうかはさておき)紹介したいな…と思います.

 

[Contents]
 

 

今回の問題

 

[問題1]

　{ \displaystyle \sqrt{n!} } が自然数となる { \displaystyle n(\geq 2) } は存在するか.

 

　{ \displaystyle n=1 } の場合は明らかに存在しますから { \displaystyle n\geq 2 } とします.

 

 

　折角なのでじっくり考えてから解答をみてください.

 

 

 

 

・・・

 

 

 

・・

 

 

 

 

・

 

 

 

 

問題1の解答

　解法は複数あるかもしれませんが, 今回は素数に注目してみます.

 

[Step1]

　{ \displaystyle \sqrt{n!} } が自然数になるためには, 少なくとも { \displaystyle n } 以下で最大の素数 { \displaystyle p } に対して { \displaystyle p^2 } が { \displaystyle n! } を割りきる, つまり

 

{ \displaystyle p^2\mid n! }

 

でなければならないことは明らかです.

　従って

 

{ \displaystyle p\leq n\lt 2p\tag{1} }

 

なる自然数 { \displaystyle n } について, { \displaystyle \sqrt{n!} } が自然数であることはありません.

　同様に, { \displaystyle p } より一つ大きい素数 { \displaystyle q } に対しても

 

{ \displaystyle q\leq n\lt 2q\tag{2} }

 

なる自然数 { \displaystyle n } について, { \displaystyle \sqrt{n!} } が自然数でないことが分かります.

 

スポンサーリンク

 

[Step2]

　Step1より, { \displaystyle p\mid n! } を満たしていても { \displaystyle p^2\mid n! } でなければ意味がありません.

　従って

 

{ \displaystyle p\mid n!\, \land\, p^2\nmid n! }

 

となるような素数 { \displaystyle p } を本記事に限り「孤立素数」と呼ぶことにします. 

 

　{ \displaystyle \sqrt{n!} } が自然数となるためには孤立素数が存在しないことが必要条件となるのは明らかです.

 

　さて(1), (2)から, 残るは { \displaystyle 2p } と { \displaystyle q } の関係次第となります.

　以下の図のように2通りが考えられるからです.

 

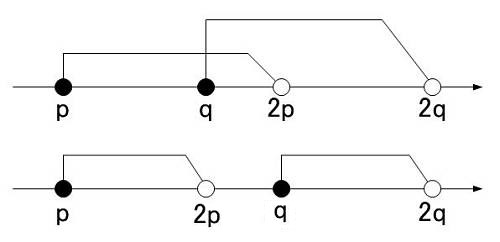
161006_07

{ \displaystyle [ 2p\geq q } のとき { \displaystyle ] }

　上記図表の上の場合ですね.

　このとき { \displaystyle 2p=q } であれば { \displaystyle n=p^2 } までの時点で { \displaystyle p } が孤立素数から脱するまでに新たな孤立素数として { \displaystyle q } が現れてしまいます.

　従ってこの状況では前後で { \displaystyle \sqrt{n!} } が自然数になることはありません.

 

 

{ \displaystyle [ 2p\lt q } のとき { \displaystyle ] }

　上記図表の下の場合です.

　このとき { \displaystyle 2p\leq m\lt q } なる自然数 { \displaystyle m } を取ることができ, このとき

 

{ \displaystyle p\mid m!\, \land\, p^2\mid m! }

 

であるため, { \displaystyle \sqrt{m!} } が自然数になる可能性が出てきます(確定ではないことに注意).

 

　しかし, ここでベルトランの仮説(チェビシェフの定理)を見てみましょう.

 

[定理：チェビシェフの定理]

　任意の自然数 { \displaystyle n } について,

{ \displaystyle n\leq p\lt 2n }

を満たす素数 { \displaystyle p } が存在する.

 

　チェビシェフの定理に出てくる素数 { \displaystyle p }, 及び自然数 { \displaystyle n } は任意ですから, { \displaystyle p } を { \displaystyle q }, { \displaystyle n } を { \displaystyle p } と置いて差し支えありません.

　つまり任意の素数 { \displaystyle p } とそれより一つ大きな素数 { \displaystyle q } について

 

{ \displaystyle p\leq q\lt 2p\tag{3} }

 

となります.

 

　しかしこの { \displaystyle (3) } は仮定と矛盾しています, 従って仮定は間違っていることになります.

 

 

　以上より, 如何なる素数 { \displaystyle p } についても, { \displaystyle \sqrt{n!} } を考える上で { \displaystyle p }, 或いは { \displaystyle q } のいづれか, または両方が孤立素数となり, { \displaystyle \sqrt{n!} } は自然数とならないことが分かります. { \displaystyle \square }

 

 

 

〆

　如何だったでしょうか？

　多分大丈夫だと思います, 昨日今日で考えたので不備があるかも.

 

　今後も面白い問題を見つけたら, 解答できるかは兎も角紹介したいと思います.

 

 

thetheorier