もう一人のY君

iPhoneアプリのレビューやアップデートレビューなどを書いています. たまに数学の記事も書きます.

もう一人のY君　MENU 　MENU

【数学】ピンポイント問題2

数学 数学-問題

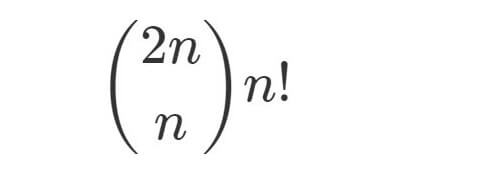
161117_00

　久しぶりのピンポイント問題, 今回は2問です.

 

[Contents]
 

 

今回の問題

　いづれも, { \displaystyle p } を奇素数, { \displaystyle n } を正整数とします.

 

[問題1]

　{ \displaystyle p=2n+1 } であるとき,

 

{ \displaystyle \binom{2n}{n}\,\equiv\,(-1)^n \pmod p }

 

 

[問題2]

　{ \displaystyle p=2n+1 } であるとき,

 

(誤) { \displaystyle \binom{2n}{n}\cdot (n!)^2\,\equiv\, n^2 \pmod p }

(正) { \displaystyle \binom{2n}{n}\cdot (n!)^2\,\equiv\, -1\pmod p }

 

(2016.12.13 訂正)

　@a_i_t_aさんより問題1のよりエレガントな証明と問題2の誤り

　　　×：{ \displaystyle p=2n+1 }

　　　○：{ \displaystyle p=2n-1 }

を指摘頂きました, ありがとうございます！.

 

(2016.12.14 訂正)

　問題2そのものの誤りを訂正しました.

　自分なりの証明を考えたかったため以下に至りましたことをお断りします.

 

　僕の思いついた以外の証明法があるのか…まだ分かりません.

 

　少し考えてみてください.

 

 

 

 

・・・

 

 

 

 

・・

 

 

 

 

・

 

 

 

 

証明

 

[問題1の証明]

blog.thetheorier.com

　結構古くなりましたが, こちらの Thm2.6より { \displaystyle p } で割り切れない自然数 { \displaystyle r }, { \displaystyle p } の指数 { \displaystyle n }, 非負整数 { \displaystyle k } について

 

{ \displaystyle \binom{rp^n-1}{k} } { \displaystyle \,\equiv\, \sum_{i=0}^{[\frac{k}{p^n}]}(-1)^{i+k}\binom{r}{i}\pmod p }

 

が成り立つことが分かっています.

　これを各々 { \displaystyle r=1, n=1, k=n } に置き変えることで

 

{ \displaystyle \binom{p-1}{n} \\ \equiv\, \sum_{i=0}^0 (-1)^{i+n}\binom{1}{i} \\ \equiv\, (-1)^n }

 

となることが分かります.

　

　{ \displaystyle p=2n+1 } より { \displaystyle p-1=2n } ですから { \displaystyle \binom{p-1}{n}\,=\,\binom{2n}{n} } , 従って

 

{ \displaystyle \binom{2n}{n}\,\equiv\, (-1)^n\pmod p }

 

となります. { \displaystyle \square }

 

 

　問題2を証明する前にある補題を紹介, 証明しておきます.

 

[補題]

　{ \displaystyle p } を奇素数とし, { \displaystyle n } を { \displaystyle p } 以下の正整数とします.

　このとき

 

{ \displaystyle \frac{1}{(p-n)!}\,\equiv\,(-1)^n(n-1)!\pmod p }

 

 

blog.thetheorier.com

　そう, これは先日紹介したこちらの記事の Prop3 です.

　ちょっと考えてみたら意外と簡単でした.

 

[補題の証明]

　いくつかの事実は今回は証明せず, 後に投稿したいと思います.

 

　まず一次合同方程式 { \displaystyle ax\equiv b\pmod m } が解を有する必要十分条件は { \displaystyle \text{gcd}(a,m)=1 } であることですね(要証明).

 

　つまり { \displaystyle \text{gcd}(a,m)=1 } のとき, 上の合同方程式は法 { \displaystyle  m } においてただ一つの解を持ちます.

 

　よってその解を { \displaystyle \frac{b}{a} } と表すことで, 有理数と同じ扱いをすることができます.

　つまり加法, 乗法として

 

{ \displaystyle \frac{a}{b}+\frac{c}{d}\,\equiv\, \frac{ad+bc}{bd}\pmod m }
{ \displaystyle \frac{a}{b}\times\frac{c}{d}\,\equiv\,\frac{ac}{bc}\pmod m }

 

とすれば良いことになります(要証明).

 

　さて本題に戻りましょう, 今回は数学的帰納法を用います.

 

[{ \displaystyle n=1 } のとき]

　このとき

 

{ \displaystyle \frac{1}{(p-1)!} \\ \equiv\,(-1)^1\cdot (1-1)!\pmod p \\ \equiv -1 }

 

, 両辺に { \displaystyle -(p-1)! } をかけて左右ひっくり返せば

 

{ \displaystyle (p-1)!\,\equiv\, -1\pmod p }

 

ですからこれはウィルソンの定理(要証明)ですので明らかに成り立ちます.

 

 

[{ \displaystyle n=k } のとき]

　{ \displaystyle n=k } のとき成り立つと仮定すると,

 

{ \displaystyle \frac{1}{(p-k)!}\,\equiv\, (-1)^k\cdot (k-1)!\pmod p }

 

ですね, これを用いると(法は省略)

 

{ \displaystyle \frac{1}{(p-(k+1))!} \\ \equiv\, (-1)^k\cdot (k-1)!\cdot (p-k) \\ \equiv\, (-1)^k \cdot (k-1)!\cdot (-k) \\ \equiv\, (-1)^{k+1}\cdot k! \\ \equiv\, (-1)^{k+1}\cdot ((k+1)-1)! }

 

ということで { \displaystyle n=k+1 } でも成立します.

 

　従って数学的帰納法により定理が証明されました. { \displaystyle \square }

 

 

スポンサーリンク

 

[問題2の証明]

　補題を用いると(法 { \displaystyle p } は省略) まず問題1より

 

 { \displaystyle \binom{2n}{n}\cdot (n!)^2\,\equiv\, (-1)^n\cdot (n!)^2 }

 

です.

　これを変形して先程の補題を適用することで

 

※下は誤りで, 枠下が訂正部分となります.

{ \displaystyle (-1)^n\cdot (n!)^2 \\ \equiv\, (-1)^n\cdot (n-1)!\cdot n\cdot n! \\ \equiv \frac{1}{(p-n)!}\cdot n\cdot n! \\  \equiv \frac{1}{(2n-1-n)!}\cdot n\cdot n!  \\ \equiv\, \frac{1}{(n-1)!}\cdot n\cdot n! \\ \equiv\, n^2\quad\square}

 

{ \displaystyle (-1)^n\cdot (n!)^2 \\ \equiv\, (-1)^n\cdot (n-1)!\cdot n\cdot n! \\ \equiv \frac{1}{(p-n)!}\cdot n\cdot n! \\  \equiv \frac{1}{(2n+1-n)!}\cdot n\cdot n!  \\ \equiv\, \frac{1}{(n+1)!}\cdot n\cdot n! \\ \equiv\, \frac{n}{n+1} \\ \equiv\, \frac{\frac{p-1}{2}}{\frac{p+1}{2}} \\ \equiv\, \frac{p-1}{p+1} \\ \equiv\, -1   \quad\square}

 

 

 

〆

　いかがだったでしょうか？他の証明法を思いついたでしょうかね？

 

　また面白い問題を見つけたら紹介したいと思います.

 

thetheorier