【数学】ピンポイント問題3

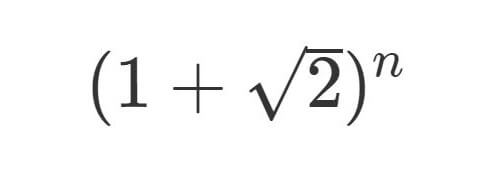
161206_00

　ピンポイント問題第3弾です.

問題

　自然数 $n$ と非負実数 $m$ について,

$(1+\sqrt m)^2 = a_n+b_n\sqrt m$

となるような実数列 $a_n, b_n$ を定めます.

　このとき

$\lim_{n \to\infty} \frac{a_n}{b_n}=\sqrt m$

であることを示してください.

　 $m=0, 1$ については自明なので証明では無視してかまいません(特に以下の証明では $m=0$ は使えない箇所があります).

　知恵袋だったか忘れましたがどこかで見たときは $m=2$ でした.

・・・

・・

・

[問題の証明]

　二項定理をうまく使います.

　任意の実数 $x$ , 自然数 $n$ について

$(1+x)^n=\sum_{k=0}^n \binom{n}{k}x^k$

ですから, $x$ に $\sqrt m$ 或いは $-\sqrt m$ を代入すると以下になります.

$(1+\sqrt m)^n$ $=\binom{n}{0}m^0+\binom{n}{1}\sqrt m+\binom{n}{ m}m$ $+\binom{n}{3}m\sqrt m+\binom{n}{4}m^2+\binom{n}{5}m^2\sqrt m+\dots$

$(1-\sqrt m)^n$ $=\binom{n}{0}m^0-\binom{n}{1}\sqrt m+\binom{n}{2}m$ $-\binom{n}{3}m\sqrt m+\binom{n}{4}m^2-\binom{n}{5}m^2\sqrt m+\dots$

　ここでさりげなく初項の $\sqrt{m}^0$ について

$\sqrt{m}^0=1=m^0$

としています.

　さてこの2式を足したり引いたりして整理すれば次を得ます.

$\frac{(1+\sqrt m)^n+(1-\sqrt m)^n}{2}$ $=\binom{n}{0}m^0+\binom{n}{2}m+\binom{n}{4}m^2+\dots$ $=\sum_{k=0}^{[\frac{n+1}{2}]}\binom{n}{2k}m^k$

$\frac{(1+\sqrt m)^n-(1-\sqrt m)^n}{2\sqrt m}$ $=\binom{n}{1}m^0+\binom{n}{3}m+\binom{n}{5}m^2+\dots$ $=\sum_{l=0}^{[\frac{n+1}{2}]}\binom{n}{2l+1}m^l$

　明らかに前者は $a_n$ , 後者は $b_n$ に相当しますね.

　従って

$\lim_{n \to\infty}\frac{a_n}{b_n}$ $=\lim_{n \to\infty} \frac{\frac{(1+\sqrt m)^n+(1-\sqrt m)^n}{2}}{\frac{(1+\sqrt m)^n-(1-\sqrt m)^n}{2\sqrt m}}$

$=\sqrt m\lim_{n \to\infty} \frac{(1+\sqrt m)^n+(1-\sqrt m)^n}{(1+\sqrt m)^n-(1-\sqrt m)^n}$

$=\sqrt m\lim_{n \to\infty}\frac{1+\left( \frac{1-\sqrt m}{1+\sqrt m} \right)^n}{1-\left( \frac{1-\sqrt m}{1+\sqrt m} \right)^n}$

$= \sqrt m\quad\square$

〆

　どこかの参考書なり試験などにありそうな問題でしたね.

もう一人のY君

iPhoneアプリのレビューやアップデートレビューなどを書いています. たまに数学の記事も書きます.

【数学】ピンポイント問題3

問題

〆