もう一人のY君

iPhoneアプリのレビューやアップデートレビューなどを書いています. たまに数学の記事も書きます.

もう一人のY君　MENU 　MENU

(数学)最大値の解釈

数学

160602_04

　当たり前に覚えているその定義が, 場合によっては都合が悪い時があります.

 

[Contents]
 

 

一般的な定義

　最小値に関する話は最大値のそれを逆にすれば良いだけなのでこの記事では最大値に関することに絞ります.

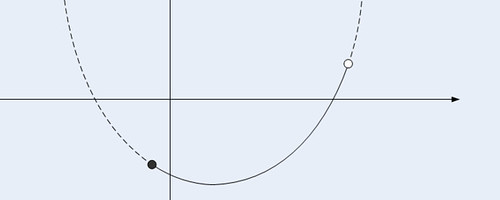
　一般的に最大値と言えば「一番大きい値」ですが, 正しい時もありますが例えば記事上に貼ったグラフの最大値はどうすれば良いでしょう？

 

 

一般的な定義が正しくない例

　例えば実数関数 { \displaystyle y = f(x) = x^{2}-1 } の, 区間 { \displaystyle [-1, 2) } における最大値を考えましょう.

　区間 { \displaystyle [-1, 2) } における { \displaystyle f(x) } の値域は今回は { \displaystyle [-1, 3) } であることはすぐに分かります.

　従って最大値は { \displaystyle x = 2 } の値 { \displaystyle f(2) = 3 } としたい所ですが, { \displaystyle f(2) = 3 } は値域 { \displaystyle [-1, 3) } の要素ではありません.

 

　仮に値が3に限りなく近いような { \displaystyle x = m_{0} } を与えてこれによる値 { \displaystyle f(m_{0}) } を最大値にしようとしても, 例えば

 

{ \displaystyle m_{0} \lt \frac{2+m_{0}}{2} \lt 2 }

 

という関係になるため, { \displaystyle f(m_{0}) } よりも大きい, 値域 { \displaystyle f([-1, 2)) } に属する値 { \displaystyle f\Bigl(\frac{2+m_{0}}{2}\Bigr) } について

 

{ \displaystyle f(m_{0}) \lt f\Bigl(\frac{2+m_{0}}{2}\Bigr) \lt 3 }

 

となってしまうため, { \displaystyle f(m_{0}) } が最大値であるという仮定に矛盾してしまいます.

　従ってどのように区間 { \displaystyle [-1, 2) } の要素を取っても, それより大きな値となる要素を取れてしまうため, 最大値が定まりません.

　よってこの場合最大値が存在しない(取れない)ことになります.

 

　そういう意味では最大値とは一番大きい値…でなく「一番小さくない値」と解釈するのが正しいでしょう.

 

 

上界と上限

　大学で学ぶ範囲になりますが, 最大値に関わるものとしてこの二つがあり, こちらから最大値(元)を定義します.

　厳密には順序集合の下で定義されますが簡単に集合とします.

 

 

上界

 集合 { \displaystyle A } について, { \displaystyle A } の任意の元 { \displaystyle y } に関して

{ \displaystyle y \leq x }

を満たす { \displaystyle x } を, { \displaystyle A } の上界と言う.

　例えば集合 { \displaystyle [-2, 3) } について, { \displaystyle x \geq 3 } を満たす任意の { \displaystyle x } は { \displaystyle [-2, 3) } の上界になります.

　上限という名前から集合のようなイメージですが集合ではありません.

 

 

上界

集合 { \displaystyle A } の上界には最小のものが存在する.

それを(集合 { \displaystyle A } の)上限と呼び, { \displaystyle \sup\{A\} } と書き表す.

　　例えば { \displaystyle [-2, 3) } といった集合であれば明らかに { \displaystyle \sup\{[-2, 3)\} = 3 } であることは明らかですが, より一般的な集合である場合を考えるとキチンと証明しなければなりません.

　また定義から分かるように, { \displaystyle \sup\{A\} } が { \displaystyle A } の元である必要はありません.

 

 

最大元

集合 { \displaystyle A } の上限 { \displaystyle \sup\{A\} } が { \displaystyle A } の元であるとき, { \displaystyle \sup\{A\} } を最大元と呼び, { \displaystyle \max\{A\} } などと書き表す.

　従って { \displaystyle \sup\{[-2, 3)\} = 3 } ですが, { \displaystyle 3 } は { \displaystyle [-2, 3) } の元でないため { \displaystyle \max\{[-2, 3)\} \neq 3 } となるわけです.

 

 

〆

　最大値や最小値が必ず存在するとは限らないこと, 分かって頂けたでしょうか？

 

 

thetheorier