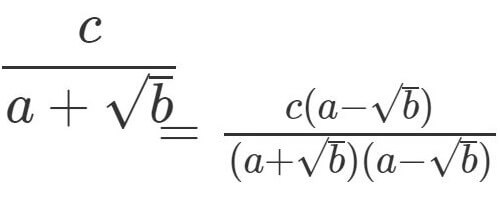
数I辺りですかね?で触れる有理化のお話.
[Contents]
有理化
有理化とは, 簡単に言えば分母が無理数となっている分数の分母分子双方に0でない実数をかけて分母を整数にすることです.
よくあるパターンが , 或いは
という形ですね.
或いは分母に三角関数などが入っている場合も考えられます.
有理化するべきかどうか
例えば はどうでしょう?
有理化すれば となるわけですが, 有理化する前は
と
, 後者は
と
でこちらの方が複雑に見えます.
見方によってどちらも都合が良いことも分かります, は単位分数ですし,
は「
の半分」とすればこちらもこちらで値のイメージがしやすいです.
或いは を有理化するとどうなるでしょう?
答えは です, 分母はスッキリしましたが分子は有理化する前の分母より複雑になってしまいました.
スポンサーリンク
どちらが求められるか
基本的に, 学校で解く問題などでは有理化で答えるケースはあろうかと思います.
しかし例えばそれが
- 解答の途中で, 有理化せずにいた方が都合がよい場合
- 必ず有理化することを求められていない場合
であれば, 見栄えを重視して敢えて行わない選択もあります.
或いは例えば三角関数を覚えるとき,
, どちらが覚えやすいか…ということでもあります.
〆
本来数学に求められるべきな一つは「分かりやすさ」, 所謂「エレガントさ」です.
出来るだけ短文で, かつ読みやすい文章が好まれます.
表記する数式も同様ではありますが, 目的が
- その数の実態を確かめること
- 出題者(教師含む)がそのように指定している(大ざっぱに言えば高校数学以下である)
ならば, 今回の話であれば有理化しておけばまず×を付けられることは無いでしょう.
もちろん特定の穴埋めのような例外は除きます.
