
こんにちは, @the_theorierです.
今回は先程紹介したアプリとほぼ並行して配布していた, 指数表を計算するアプリの修正版です.
指数表とは
念のため指数表について簡単に触れておきます, よく分からない人は飛ばしましょう(分からない人がこれを使うとは思えませんが…w).
指数表は原始根に関わるものであり, 素数pと互いに素な整数a(>1)について,
ar ≡ 1 (mod p)
を満たす正指数rが存在することはよく知られています.
フェルマーの定理よりその候補として r = p-1 が挙がるのは明らかであり, 特に r より小さい正指数で, このような式が成り立つものが無い場合, 「aが指数rに対応する」と言います, 言いかえればaの累乗を考えるとき, r乗になって初めて1と合同になる…ということですね, これは「1の原始n乗根」に近いものがあります.
ここで「aが指数p-1に対応する」とき, aを(pを法としての)原始根と呼びます.
素数pにおける原始根rは複数存在する場合があり, その一つを取ると
1, r, r2, ..., rp-2
は既約代表の一組になります.
つまり1, 2, ..., p-2 とこの組とを一対一に対応させることが出来ます, 言いかえれば「翻訳」できるようになります.
従ってrを素数pの原始根とすると, 任意の a≠0 (mod p)に関して
rα ≡ a (mod p)
を満たす指数 α が 0≦α<p-1 の範囲に必ず, ただ一つ存在します.
このαを, rを底とするaの指数(index)と呼び, Indr(a) と書き表します.
そしてこのaとIndr(a)との対応を表にしたのが指数表というわけですね.
例えば素数5, 原始根2を考えると,
20 = 1
21 = 2
22 = 4
23 = 8 ≡ 3 (mod 5)
となるので, この場合の指数表は下のようになります.
| n | 1 | 2 | 3 | 4 |
| Ind(n) | 0 | 1 | 3 | 2 |
これを作るに至ったのは, もちろんBCBの勉強もでしたが, ちょっとした数学の個人研究(独学レベル)で必要になったからでした.
色んな指数表を見たかったんですが, 毎度手書きで計算するのは面倒だし, ネットでもそれらしいのは見当たらなかったので, 自分で作ってしまった…というわけです.
アプリケーションについて
ダウンロードは下からどうぞ.
先程の数論的関数と同じく, Onedriveのzipファイルになります. 適当な場所にダウンロードして解凍, gensikon_0_1_1.exeで起動します.
こちらもインストーラーとかそういう類ではありませんので, アンインストールはフォルダごと削除するだけです.
こちらもセキュリティソフトが邪魔したりする場合があります, 「実行」か「管理者として実行」で進んでください.
仕様
シンプルに, 左上に素数を入力し, その右にある「計算」ボタンを押すだけです.
細かい演算を省略するため, 原始根は強制的に「その素数の原始根のうち一番小さいもの」になります.
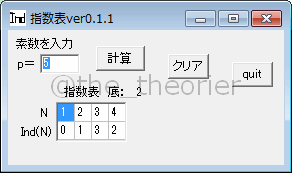
例えば素数5でやってみると, さっきのとちゃんと合ってますね.
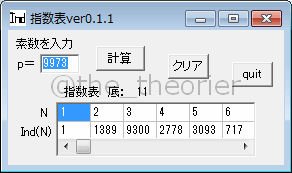
因みにこのアプリでは素数の値を4桁に制限しています, 実際には上に見える p=9973 までとなります.
これでも計算結果が出るまでに5~8分程度かかります, 「待てる」範囲は2500前後になります, というか2500前後まででも普通に使うなら十分だよね.
本当は任意の原始根で作れるようにしたかったんですが, まぁ簡単に実践出来れば苦労しないですよね…
因みにアイコンデザインは数分で描いたものなのでセンスの欠片もありません.
更新
更新内容は先程投稿した数論的関数と同様です.
〆
これも悪用しない範囲で使ってくださいね, 特に大学生のみんな☆(ゝω・)v
