もう一人のY君

iPhoneアプリのレビューやアップデートレビューなどを書いています. たまに数学の記事も書きます.

もう一人のY君　MENU 　MENU

二項係数剰余

数学

　こんにちは, @the_theorierです.

 

　今回は別サイトで書いたものの焼き直しです.

 

スポンサーリンク

 

 

　きっかけは日本評論社さんの数学セミナーさんの「エレガントな解答を求む」の一節にあった補題です(2009年6月号より).

 

 150727_01

 　ふと思ったのは, 「これをもっと一般化出来ないかな」…というものでした.

 

 　それから数年程かけてある程度まで消化できたわけです.

 

　数学の醍醐味は, こうやって自分で問題提起して証明まで与えることが出来る点ですね.

 

　上のThm1.1の証明はこれから証明する定理の一部になるので, この場での証明は割愛します.

 

 

　ではさっそく紹介するんですが, いくらか場合分けされており, また証明に必要な定義, 補題があるのでまずそちらから紹介します.

 

定義・断り・補題など

　まず証明にあたって, 基本的には合同式を使います.

　合同式の法は素数 p のみを扱います, 合成数は扱いません, また法の表記は必要に応じて省略します.

　二項係数 { \displaystyle \binom{m}{k} }について,  m≧k であることは自明であるとします.

 　加えると m, k は { \displaystyle 0\leq k\leq \dfrac{m}{n} }  であることが分かりますので k はこの範囲内の非負整数として扱います.

 　実数 x に対して { \displaystyle \left[ x \right] }をガウス記号, 別の呼び方をすれば床関数とします.

 

　そして次が重要ですが, 定理によって m の p による一意分解を次の2通りで定めます.

 

[Def1.1]

・q : m の正値最小剰余, 一般に言う「mをpで割った余り」.

・r : m-q の素因数のうち, pを除いたものの総積.

・n := { \displaystyle \log _{p}\dfrac{m-q}{r} } 

　以上を使って

{ \displaystyle m=rp^{n}+q } 

と一意分解します.

 

　例えば m=32, p=5 なら,

　32-2=30=5*6 より q=2.

　m-q=32-2=30=2*3*5より r=2*3=6.

　{ \displaystyle \dfrac{m-q}{r} = \dfrac{30}{6} = 5 } の指数は1 なので n=1.

　よって 32 = 6*51+2 となります.

 

 [Def1.2]

・q : m の負値最大剰余(x≡m (mod p) となる xのうち, 負で最大のもの)に -1 を掛けたもの.

・r : m+q の素因数のうち, p を除いたものの総積.

・n := { \displaystyle \log _{p}\dfrac{m+q}{r} } 

　以上を使って

{ \displaystyle m=rp^{n}-q }

と定めます.

 

 　いづれも場合もそれぞれの q, r, n が一意に決まる事が分かります.

 

 　また q の表記がある場合, 予め q ≠ 0 であることを断わっておきます, つまり q = 0 であるときは q を表記しません.

 

　ここからは証明に必要な補題になります, 度々省略しますがご了承を.

 

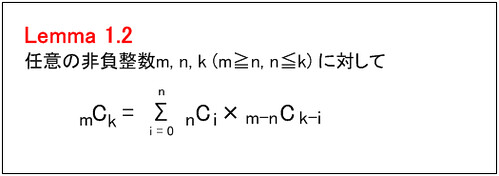
 150727_02

 (Lemma 1.2 の証明)

　二項係数に関する性質

{ \displaystyle \binom{m}{k} = \sum ^{n}_{i=0}\binom{n}{i}\times \binom{m-n}{k-i} }

と数学的帰納法から導かれます. □

 

 150727_03

 (Lemma 1.3 の証明)

　上記でも使った二項係数の性質を少し変形させた

{ \displaystyle \binom{m}{k} = \binom{m+1}{k} - \binom{m}{k-1} } 

と数学的帰納法を用いることで

{ \displaystyle \binom{m}{k} = \sum ^{n}_{i=0}(-1) ^{i} \binom{m+1}{k-i} + (-1) ^{n+1} \binom{n}{k-n-1}  (n\in \mathbb{Z} ^{+}) } 

を得ます.

　ここに n = k-1 を代入して望む等式を得ます. □

 

 　以上を使って話を進めます.

　まず p を奇素数とし, p=2 の場合を分けることにします.

　なお「∃A st. B」という記述は「BとなるAが存在する」を意味しています, otherwiseとは「その他」です.

 

 

p が奇素数の場合

 

 150727_04

 (Thm 2.1 の証明)

　まず前者を考えます.

　a = 0, r についてはそれぞれ

{ \displaystyle \binom{rp}{0} = 1 = \binom{r}{0} }

{ \displaystyle \binom{rp}{rp} = 1 = \binom{r}{r} }

と出来るので自明に成り立ちます.

　a ≠ 0, r の場合を数学的帰納法で考えます, a = 1 の場合は Lemma 1.2 で n = p とすることで

{ \displaystyle \binom{rp}{p} } 

{ \displaystyle =\sum ^{p}_{i=0} \binom{p}{i}\binom{p}{p-i} } 

{ \displaystyle ≡\binom{(r-1)p}{p} + \binom{(r-1)p}{p}  }　(Thm1.1(1) より) 

{ \displaystyle ≡\binom{(r-1)p}{p} + 1 }

{ \displaystyle ≡(\binom{(r-2)p}{p} + 1) + 1 }　(上2式の関係より)

{ \displaystyle ≡… }

{ \displaystyle ≡\binom{(r-(r-1))p}{p} + (r-1) }

{ \displaystyle ≡\binom{p}{p} + (r-1) }

{ \displaystyle ≡1 + (r-1) }

{ \displaystyle ≡r }

{ \displaystyle ≡\binom{r}{1} }        

 

で成り立ちます.

　一般の a = n で成り立つと仮定すると,

{ \displaystyle \binom{rp}{(n+1)p} }

{ \displaystyle =\binom{(r-1)p}{p} } 

{ \displaystyle ≡\binom{(r-1)p}{p} + \binom{r-1}{n} }　(仮定より)

{ \displaystyle ≡\binom{(r-2)p}{p} + \binom{r-2}{n} + \binom{r-1}{n} }

{ \displaystyle ≡… }   

{ \displaystyle ≡\binom{(r-(r-n-1))p}{(n+1)p} + \sum ^{r-1}_{i=n}\binom{i}{n} }

{ \displaystyle ≡1 + \sum ^{r-1}_{i=n+1}\binom{i}{n}　≡　\sum ^{r-1}_{i=n}\binom{i}{n} }

{ \displaystyle ≡\binom{(r-1)+1}{n+1}　　(\sum ^{n}_{i=m}\binom{i}{m} = \binom{n+1}{m+1} }　より) 

{ \displaystyle ≡\binom{r}{n+1} } 

より成り立つことが分かります.

 

　次に k = ap なる a が存在しないときを考えます, このとき

{ \displaystyle B = \binom{rp}{k} } 

とおくと

{ \displaystyle \dfrac {rp}{k}g　(g := \binom{rp-1}{k-1}) } 

と出来るので

kB = rpg

, これは kB が p の倍数であることを意味しています.

　しかし仮定から k は p の倍数ではありませんから, B が p の倍数であることが分かります.

　従って

{ \displaystyle B = \binom{rp}{k} ≡ 0 } 

となります. □

 

 150727_05

 (Thm 2.2 の証明)

　まず前者を証明します.

　a = 0, r については先程同様,

{ \displaystyle \binom{rp ^{n}}{0} = 1 = \binom{r}{0} }

{ \displaystyle \binom{rp ^{n}}{rp ^{n}} = 1 = \binom{r}{r} }

 から直ちに得られます.

　a = 1, 2, ..., r-1 についても Thm 2.1 を参考にすると

{ \displaystyle \binom{rp ^{n}}{ap ^{n}} = \binom{rp ^{n-1}\times p}{ap ^{n-1}\times p} }

{ \displaystyle ≡\binom{rp ^{n-1}}{ap ^{n-1}} }

{ \displaystyle ≡… }

{ \displaystyle ≡\binom{r}{a} }

で成り立ちます.

　k が { \displaystyle p ^{m}  } (1≦m<n)の倍数のとき, 

{ \displaystyle B = \binom{rp ^{n}}{Kp ^{n}}　(K }は{ \displaystyle k = Kp ^{m} }を満たす整数)

 とおくと

{ \displaystyle B = \dfrac{rp ^{n}}{Kp ^{m}} g　(g := \binom{rp ^{n-1}-1}{Kp ^{m-1}-1}) }

となるので

{ \displaystyle KB = rp ^{n-m}g }

を得ます, これは KB が { \displaystyle p ^{n-m} }(≧p) で割り切れることを意味しています.

　しかし K は定義より p で割り切れないので, 代わりに B が p の倍数であることになります, よって

{ \displaystyle B = \binom{rp ^{n}}{Kp ^{m}} ≡ 0 }

を得ます. □

 

 150727_06

 (Thm 2.3 の証明)

　q = 1 の場合は自明なので省略します.

　Lemma 1.2 において n = q とすると上記左辺は

{ \displaystyle \binom{rp ^{n}+q}{q} = \sum ^{q}_{i=0}\binom{q}{i} \binom{rp ^{n}}{q-i} }

となります, 上記右辺の一部は Thm 2.2 より

{ \displaystyle \binom{rp ^{n}}{q-i} ≡ 0　(i = 1, 2, ..., q-1) }

ですから,

{ \displaystyle \binom{rp ^{n}+q}{q} }

{ \displaystyle ≡ \binom{q}{q} \times \binom{rp ^{n}}{q-q} }

{ \displaystyle ≡ 1 }

より成り立ちます. □

 

 150727_07

 (Thm 2.4 の証明)

　Lemma 1.2 より

{ \displaystyle \binom{rp ^{n}+q}{k} = \sum ^{q}_{i=0}\binom{q}{i} \binom{rp ^{n}}{k-i} }

であり, 右辺を観察すると, k-i = k-q, k-q-1, ..., k-1 の中に

{ \displaystyle Kp ^{n} }

という形の数が存在するならば, それは高々一つであり, もし存在するならThm 2.2 の証明の前半から

{ \displaystyle \binom{rp ^{n}}{k-i} ≡ \binom{r}{K} }

であり, それ以外の項については同じく Thm 2.2 から 0 と合同になります.

　i は 0≦i≦q を満たしていますから, 上記のような i が存在するならば, K は

{ \displaystyle k-q \leq Kp ^{n} \leq k }

{ \displaystyle ⇔ \dfrac{k-q}{p ^{n}} \leq K \leq \dfrac{k}{p ^{n}} }

を満たしていることになります.

　従ってこのような K が存在する場合, { \displaystyle k-i = Kp ^{n} }, つまり { \displaystyle i = k-Kp ^{n} } より

{ \displaystyle \binom{rp ^{n}+q}{k} }

{ \displaystyle ≡ \binom{q}{k-Kp ^{n}}\times\binom{rp ^{n}}{Kp ^{n}} }

{ \displaystyle ≡ \binom{q}{k-Kp ^{n}}\binom{r}{K} }　(Thm 2.2 より)

 

となります.

　もしこのような K が存在しなければ, すべての i について { \displaystyle \binom{rp ^{n}}{k-i} ≡ 0 }ですから,

{ \displaystyle \binom{rp ^{n}}{k} }

{ \displaystyle ≡ \sum ^{q}_{i=0}\binom{q}{i}\binom{rp ^{n}}{k-i} }

{ \displaystyle ≡ \sum ^{q}_{i=0}(\binom{q}{i}\times 0) }

{ \displaystyle ≡ 0 }

となります. □

 

 150727_08

 (Thm 2.5 の証明)

　二項係数の定義より

{ \displaystyle k!\times \binom{rp ^{n}+q}{k} }

{ \displaystyle = (rp ^{n}+q)\times (rp ^{n}+q-1)\times ...\times (rp ^{n}+q-k+1) }

{ \displaystyle ≡ q\times (q-1)\times ...\times (q-k+1) }

{ \displaystyle ≡ {}_q \mathrm{P}_k }

となるので, 改めて書くと

{ \displaystyle k!\times \binom{rp ^{n}+q}{k} ≡ {}_q \mathrm{P}_k }　…(※)

ですね.

　仮定から k＜q＜p なので k と p は互いに素であり, また二項係数の性質から { \displaystyle {}_q \mathrm{P}_k } は k! で割り切れます.

　よって(※)は法を保ったまま, 両辺を k! で割ることができます, つまり

{ \displaystyle \binom{rp ^{n}+q}{k} }

{ \displaystyle ≡ \binom{rp ^{n}}{k} }

{ \displaystyle ≡ \dfrac{{}_q \mathrm{P}_k}{k!} }

{ \displaystyle ≡ \binom{q}{k} }

となります. □

 

 150727_09

 (Thm 2.6 の証明)

　k の偶奇で場合分けします.

(k が奇数のとき)

k = 2t-1

とでもおき, Lemma 1.3 を適用すると

{ \displaystyle \binom{rp ^{n}-1}{k} = \sum ^{2t-1}_{i=0}(-1) ^{i}\binom{rp ^{n}}{2t-1-i} }

となります.

　Thm 2.2 より, 上記右辺の各項のうち { \displaystyle \binom{rp ^{n}}{2t-1-i} } の部分が 0 以外と合同になるのは, 2t-1-i が { \displaystyle p ^{n} } の倍数であるときのみであり, 存在するならばそれは

{ \displaystyle 0, p ^{n}, p ^{2n}, …, \left[ \dfrac{2t-1-i}{p ^{n}} \right] p ^{n}  }

の  { \displaystyle \left[ \dfrac{2t-1-i}{p ^{n}} \right] +1 } 個になります.

　それ以外は Thm 2.2 より 0と合同ですから,

{ \displaystyle \binom{rp ^{n}-1}{2t-1} ≡ \sum ^{\left[ \dfrac{2t-1}{p ^{n}} \right]}_{i=0}(-1) ^{i+1}\binom{r}{i} }

とできます.

 

(k が偶数のとき)

　こちらも奇数の場合と同じく, 例えば k = 2s とでも置くことで

{ \displaystyle \binom{rp ^{n}-1}{2s} ≡ \sum ^{\left[ \dfrac{2s}{p ^{n}} \right]}_{i=0}(-1) ^{i+1}\binom{r}{i} }

を得ます(偶奇での違いはΣの中の(-1)の指数です).

　2式をまとめて定理を得ます. □

 

 150727_10

 (Thm 2.7 の証明)

　二項係数について

{ \displaystyle \binom{m}{k} = \dfrac{k+1}{m+1}\binom{m+1}{k+1} }

が成り立つことを利用して,

{ \displaystyle \binom{rp ^{n}-q}{k} }

{ \displaystyle = \dfrac{k+1}{rp ^{n}-(q-1)}\times \dfrac{rp ^{n}-(q+k-1)}{k+1}\times \binom{rp ^{n}-(q-1)}{k} }

{ \displaystyle = \dfrac{rp ^{n}-(q+k-1)}{k+1}\times \binom{rp ^{n}-(q-1)}{k} }

, よって

{ \displaystyle  (rp ^{n}-(q-1)) \times \binom{rp ^{n}-q}{k} = (rp ^{n}-(q+k-1)) \times \binom{rp ^{n}-(q-1)}{k} }

{ \displaystyle ⇒ (q-1) \binom{rp ^{n}-q}{k} ≡ (q+k-1) \binom{rp ^{n}-(q-1)}{k} }

となります.

　ここで簡単のために

{ \displaystyle λ(s) := \binom{rp ^{n}-(q-s)}{k}　(s = 0, 1, 2, …, q-2) }

 とおくことにすると, 例えば最後の合同式は

(q-1)λ(s) ≡ {q+k-(s-1)}λ(s+1)

と書けます.

　具体的に s = 0, 1, 2, …と書き下すと

(q-1)λ(0) ≡ (q+k-1)λ(1)　…[1]
(q-2)λ(1) ≡ (q+k-2)λ(2)　…[2]
(q-3)λ(2) ≡ (q+k-3)λ(3)　…[3]
…

…となります.

　[1]の両辺を (q-2) 倍し, [2] を代入すると

(q-2)(q-1)λ(0) ≡ (q+k-1)(q-2)λ

⇔　(q-2)(q-1)λ(0) ≡ (q+k-1)(q+k-2)λ(2)

ですね, これを更に (q-3) 倍し, [3] を代入すると

(q-3)(q-2)(q-1)λ(0) ≡ (q+k-1)(q+k-2)(q-3)λ(2)

⇔　(q-3)(q-2)(q-1)λ(0) ≡ (q+k-1)(q+k-2)(q+k-3)λ(3)

となります, これを s = q-2 まで行えば, 帰納的に

{ \displaystyle {}_{q-1} \mathrm{P}_{q-1} λ(0) ≡ {}_{q+k-1} \mathrm{P}_{q-1} λ(q-1) }

{ \displaystyle ⇔ (q-1)! \times λ(0) ≡ {}_{q+k-1} \mathrm{P}_{q-1} λ(q-1) }

 を得ます.

　定義より q＜p ですから, (q-1)! と p は互いに素, ゆえに法p のまま両辺を (q-1)! で割って

{ \displaystyle λ(0) = \binom{rp ^{n}-1}{k} }

{ \displaystyle ≡ \dfrac{{}_{q+k-1} \mathrm{P}_{q-1}}{(q-1)!}\times λ(q-1) }

{ \displaystyle ≡ \binom{q+k-1}{q-1}\binom{rp-1}{k} }.　□

 

 150727_11

 (Corollary 2.8 の証明)

Thm 2.6, および Thm 2.7 を組み合わせれば得られます. □

 

 

 　以上で p が奇素数である場合は終わりです, 次に p = 2 である場合を考えます.

 

 

p = 2 の場合

 　法2 の既約剰余系とはつまるところ例えば {-1, 0, 1} といったシンプルなものですから, 任意の非負整数 m の一意分解は

{ \displaystyle m = r2 ^{n}+q　(r }は奇数, { \displaystyle q \in \left\{ -1, 0, 1 \right\} ) }

として十分であることが分かります.

　また証明自体は p が奇素数である場合とほとんど同じで, 定理の数が一つ減るだけになりますので, 定理を紹介するのみで証明はすべて割愛することにします.

 

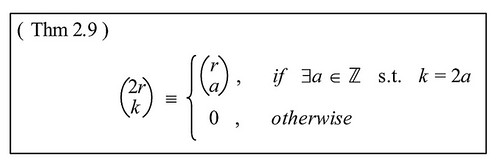
 150727_12 

 

 150727_13

 

 150727_14

 

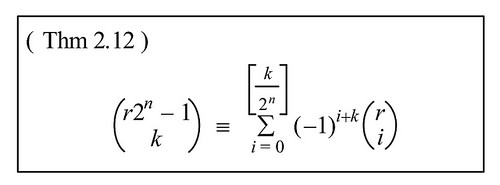
 150727_15

 

 

 　以上になります.

　これらの証明まで考え付くのに3～4年(訂正含む)ほどはかかりましたね, もちろん毎日やってるわけじゃないので実際に費やした時間は遥かに少ないですが…

 

　定理が分かっていて証明するのと, 命題を推論して, かつ証明するのではその手間が比較にならないほど違います, しかし一つでも考え付けば「夏休みの宿題」にはもってこいかもしれませんね, 以上を丸パクリするためにここに改めて書いたつもりではありませんが, こういう「他の人と違う」ネタで行ってみるのもお勧めですよ.

　因みにこれらは合同式を使わなくてもなんとかなります, アイデアというかひらめき次第です.

 

実際に試してみる

　折角なので本当に使えるか試してみましょう.

　試しに { \displaystyle \binom{523}{13}  = 30265571496378712913548416 } を 31 で割った余りを, Corollary 2.8 を利用して出してみます.

 

　まず523を 31 で割った余りは 27, よって q = 4 になります.

　523 + 4 = 527 は 17*31 と素因数分解されるので r = 17, n = 1 が分かります.

　k = 13 に対して { \displaystyle p ^{n} = 31 ^{1} } の方が大きいですから { \displaystyle \left[ \dfrac{k}{p ^{n}} \right] = 0 } です, よって右辺のΣの項は { \displaystyle (-1) ^{0}\binom{r}{0} } のみとなります

　よって

 

{ \displaystyle \binom{523}{13} }

{ \displaystyle ≡ (-1) ^{13}\binom{4+13-1}{13}\times 1 }

{ \displaystyle ≡ (-1)\binom{16}{13} }

{ \displaystyle ≡ (-1)\binom{16}{3} }

{ \displaystyle ≡ (-1)\dfrac{16\times 15\times 14}{3\times 2\times 1} }

{ \displaystyle ≡ (-16)\times 35 }

{ \displaystyle ≡ 15\times 4 }

{ \displaystyle ≡ 60 }

{ \displaystyle ≡ 29 }

 

でどうやら 29 になるようです.

 

　実際確かめると

 

30265571496378712913548416 = 976308757947700416566077 * 31 + 29

 

になります.

 

 

まだ完全ではない

　一通りこれで対応できているように見えますが実際のところまだ不完全です.

　例えば { \displaystyle \binom{12}{5} } を 29 で割った余りを考えると, Corollary 2.8 の後半より,

 

{ \displaystyle \binom{12}{5} }

{ \displaystyle = \binom{29-14}{5} }

{ \displaystyle ≡ (-1) ^{5}\times \binom{14+5-1}{5}\times 1 }

{ \displaystyle ≡ (-1)\times \binom{18}{5} }

 

となって, 寧ろ計算量が増えています.

 

　これは m に対して 素数p が大きすぎることが原因であり, 大雑把に m＜2p の場合で起こる事がわかります.

 

　この場合についてはまだ自分の中では解決していません.

　興味のある方は試してみてはどうでしょう？(他力本願)

 

 

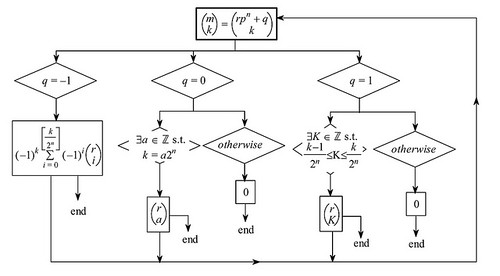
流れ図

　以上の流れを簡単に図式してあります, 最後にどうぞ.

 

p が奇素数の場合

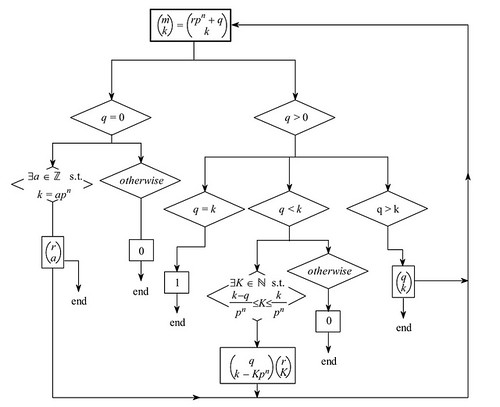
 150727_16

 

p = 2 の場合

 150727_17

 

 　以上で終わりです, では.

thetheorier