もう一人のY君

iPhoneアプリのレビューやアップデートレビューなどを書いています. たまに数学の記事も書きます.

もう一人のY君　MENU 　MENU

合同式

数学

 151005_00

　こんにちは, @the_theorierです.

 

　今回は合同式の基本に触れたいと思います.

 

倍数, 約数

　まず倍数と約数についてです.

 

　以前, 整数 { \displaystyle a, b } との間に { \displaystyle a = bq + r } を満たす整数 { \displaystyle q, r } の組がただ一つ存在することを紹介しました.

thetheorier.hatenablog.com

 

　また整数は必ずしも割り算を行えません, つまり代数学的に「除法で閉じていません」.

　理由は解釈によっては上の理屈で { \displaystyle r \neq 0 } の場合があるからです.

　シンプルに言えば, ある整数 { \displaystyle a, b } について, { \displaystyle a = bq } を満たす整数 { \displaystyle q } が存在するとは限りません.

　より易しく言えば { \displaystyle \dfrac{a}{b} (b\neq 0) } が整数であるとは限りません.

 

　そこで整数 { \displaystyle a, b (b \neq 0) } について, ある整数 { \displaystyle q } が存在して

 

 { \displaystyle a = bq }

 

 を満たしているとき, "{ \displaystyle a } は { \displaystyle b } の倍数", 或いは"{ \displaystyle b } は { \displaystyle a } の約数", "{ \displaystyle b } は { \displaystyle a } を割りきる(～で割り切れる)"と言います. 

 

「余り」について

　我々は合同式を学ぶ前に「余り」を学びます.

　一般に { \displaystyle a = bq + r } であるとき, これを「{ \displaystyle a } を { \displaystyle b } で割った余りが { \displaystyle r }」であるとし, しばしば

 

{ \displaystyle a÷b = q　…　r }

 

 と書きます.

　また初等時は整数でなく自然数として学びます.

　これは教える(教わる)上で次第に拡張した方が都合がよい等々の事情があるわけですが, 場合によってはその時点で凝り固まってしまったり, 拡張概念を理解するのに時間を浪費してしまう可能性もあります.

 

　実際高校数学然り, 合同式の定義として例えば

 

{ \displaystyle a } を { \displaystyle m } で割った余りが { \displaystyle b } であるとき,

{ \displaystyle a ≡ b　(\text{mod}\ m) }

 

であったり, 或いは

 

{ \displaystyle a } と { \displaystyle b } を { \displaystyle m } で割った余りがそれぞれ等しいとき,

{ \displaystyle a ≡ b　(\text{mod}\ m) }

 

 であったりします.

 

 　もちろん理解する上では良いと思います, 後述する通りで合同式はこの余りの概念の拡張ですから.

 

　しかし"余り"を前提に扱う場合, { \displaystyle a, b } は自然数(非負整数)であることが多いです, 例えば { \displaystyle 1 ≡ 3　(\text{mod}\ 2) } であったり { \displaystyle -2 ≡ 5　(\text{mod}\ 3) } といった式を, 上記の定義でどう説明すれば良いでしょうか？

 

 

　これは極論でも何でもなく, ごくごく当たり前に扱う事になる問題です, なので僕が合同式を説明する場合は, "これまでの余りの概念に拘るのは良くない"と指摘することがあります.

 

 

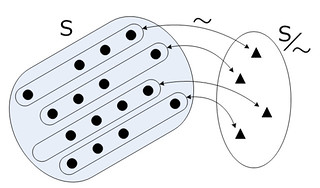
同値関係

　我々は普段, 等しいかそうでないか…で主に二つの対象を比較します.

　しかし場合によっては特定の条件を満たす場合に同じと「みなす」ことがあります.

　それを公理化させたものが同値関係の考え方です.

 

 　集合 { \displaystyle S } の任意の要素 { \displaystyle a, b } による条件, 式などをここでは { \displaystyle a～b } と書き, { \displaystyle ～ } を"({ \displaystyle S }上の)関係"と呼びます.

　{ \displaystyle S } 上の任意の要素 { \displaystyle a, b, c } が以下を満たすとき, { \displaystyle ～ } を({ \displaystyle S }上の)"同値関係"と呼びます.

 

 { \displaystyle (1)　a～a }

{ \displaystyle (2)　a～b　⇒　b～a }

{ \displaystyle (3)　a～b, b～c　⇒　a～c }

 

 　人によっては { \displaystyle a～b } でなく { \displaystyle a\text{R}b } などと書いたりします.

 

 

合同式

 　先程の { \displaystyle a = bq + r } では, 与えられた { \displaystyle a, b } に対して余り { \displaystyle r } が一つに定まるものでした.

 

 　では, ここで除数(ここでは { \displaystyle b })を固定して考えるとどうなるでしょうか？

 

 　例えば以下のように変形してみましょう.

 

{ \displaystyle a = bq + r }

{ \displaystyle ⇔　a-r = bq }

 

 　言ってみればこれは「{ \displaystyle a-r } は { \displaystyle b } の倍数である…ということです.

 

 　これをもとにすると, 任意の整数 { \displaystyle k } について

 

{ \displaystyle a = bq + r　ならば　(a+k) - (r+k) = bq }

 

 とも書けます.

 

　つまり二つの組 { \displaystyle (a, b), (a+k, b+k) } は, 「{ \displaystyle b } の倍数であること」を前提にすると同じであるとみなすことができます.

 

　ハッキリ言ってしまえば, 「二数の差が除数の倍数であること」を条件とする関係, 同値関係が作れるわけです.

　そしてそれが本来の合同式となるわけです.

 

 

合同式の定義

 　二つの整数 { \displaystyle a, b } の差 { \displaystyle a-b } が整数 { \displaystyle m } の倍数であるとき,

 

{ \displaystyle a≡b　(\text{mod}\ m) }

 

 と書き表し, 「{ \displaystyle a } と { \displaystyle b } は(法 { \displaystyle m } に関して)合同である」と言います.

 

 　例えば { \displaystyle 1-3 = -2 = 2\times (-1) } なので定義から { \displaystyle -1 ≡ 3　(\text{mod}\ 2) } となりますね.

 

　合同式は同値関係を満たしています, ようは同値関係の3つの条件が成り立っています.

　試しに確認してみてください.

 

 

合同式の解釈

　合同式は結局何なんでしょうか?

　簡単に言えば, 「差を取って除数の倍数になる二数は, ”その世界では”同じもの」ということです.

 

 　合同式で一番分かりやすいのは「曜日」ですね.

　例えばある月の1日と8日は明らかに違う日です.

　しかし曜日とは言ってみれば法7の合同式のようなものです,  { \displaystyle 1-8 = -7 = 7\times (-1) } ですから { \displaystyle 1 ≡ 8　(\text{mod}\ 7) }, つまり"同じ曜日"というわけです.

 

　日付としては事なりますが, 曜日で考えれば同じであると"みなせる"わけですね, この考えが合同式であり, ひいては同値関係の理屈です.

 

 　また当然ですが { \displaystyle a ≡ b　(\text{mod}\ m) } において { \displaystyle a, b } を自然数, かつ { \displaystyle 0 \leq b＜m } とすれば, 俗に言う「{ \displaystyle a } を { \displaystyle m } で割った余りは { \displaystyle r }」になります.

 

 

 

〆

 　某アニメよろしく, 「モジュロ演算」とか「モジロ演算」などと呼ばれることがありますが, 大学にいた間にそんな言葉を聞いたことも使ったこともありませんね…

　最近では知りませんが.

thetheorier