【数表】加法的関数・乗法的関数

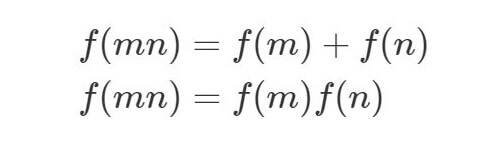
161001_00

　今回の数表は加法的関数, そして乗法的関数です.

[Contents]

加法的関数、乗法的関数とは
- 数論的関数、加法的関数、乗法的関数
- 加法的関数、乗法的関数の例
加法的関数数表
- n=1～50
- n=50～100
乗法的関数数表
- n=1～50
- n=50～100
〆

加法的関数、乗法的関数とは

　これらの言葉は主に数論という分野で使われます.

　特定の性質を持つ関数は議論の対象となりやすいからですね.

数論的関数、加法的関数、乗法的関数

　その前に数論的関数から説明しましょう.

[定義：数論的関数]

　正整数 $Z^+$ から複素数 $\mathbb{C}$ への関数

$\mathbb{Z}^+\to\mathbb{C}$

を, 数論的関数と言う.

　このうち, 以下の性質を持つ関数をそれぞれ加法的関数, 乗法的関数と言います.

[定義：加法的関数]

　数論的関数 $f(x)$ が以下を満たすとき, $f(x)$ は加法的関数と言う：

　互いに素である任意の整数 $m, n$ について

$f(mn)=f(m)+f(n)$

[定義：乗法的関数]

　数論的関数 $f(x)$ が以下を満たすとき, $f(x)$ は乗法的関数と言う：

　互いに素である任意の整数 $m, n$ について

$f(mn)=f(m)f(n)$

　これらを満たす数論的関数で更に特徴的であるものは更に議論の対象になりやすいですね.

加法的関数、乗法的関数の例

　2つの例としては以下があります(今回取り上げるものになります, $n$ ) は正整数.

　ここで $p, q, r$ を相異なる素数, $a, b, c$ を非負整数とし, $n=p^a q^b r^c\dots$ と素因数分解できるとします.

[加法的関数]

$\Omega(n)$ ：ビッグオメガ関数, $n$ の素因数の, 重複を含めた総和

　(例) $\Omega(20)=\Omega(2^2\times 5)=2+5=10$

　 $\Omega(n)=a+b+c+\dots$ が成り立ちます.

$\omega(n)$ ：オメガ関数, $n$ の異なる素因数の総数

　(例) $\omega(20)=\omega(2^2\times 5)=2$

　 $\omega(n)=\#\{ p \mid p|n \}$ が成り立ちます.

$\text{sopf}(n)$ ： $n$ の異なる素因数の総和

　(例) $\text{sopf}(20)=\text{sopf}(2^2\times 5)=2+5=7$

$\text{sopfr}(n)$ ： $n$ の素因数の, 重複を含めた総和

　(例) $\text{sopfr}(20)=\text{sopfr}(2^2\times 5)=$ $2+2+5=9$

[乗法的関数]

$d(n)$ ： $n$ の正約数の個数

　(例) $20$ の正約数は $1, 2, 4, 5, 10, 20$ の　 $6$ つだから, $d(20)=6$ .

　 $d(n)=\#\{ m\in\mathbb{Z}^+ \mid m|n \}$ が成り立ちます.

$\sigma(n)$ ： $n$ の正約数の総和

　(例) $20$ の正約数は $1, 2, 4, 5, 10, 20$ だから, $d(20)=1+2+4+5+10+20=42$ .

　 $\sigma(n)=\sum_{m\in\mathbb{Z}^+ , m|n } m$ が成り立ちます.

$\varphi(n)$ ：オイラーのφ関数, $1$ から $n$ までの自然数のうち, $n$ と互いに素な数の個数.

　(例) $20$ までの非負整数のうち, $20$ と互いに素なのは $1, 3, 7, 9, 11, 13, 17, 19$ の8個である, よって $\varphi(20)=8$ .

$\varphi(p^a)=p^a - p^{a-1}$

, また互いに素な非負整数 $m, n$ について

$\varphi(mn)=\varphi(m)\varphi(n)$

が成り立ちます(乗法的関数そのもの).

$\mu(n)$ ：メビウス関数, $n$ が平方数で割り切れるとき $0$ , それ以外のとき, $n$ が異なる $k$ 個の素数で素因数分解されるとき, $\mu(n)=(-1)^k$ .

　(例) $20$ は平方数 $4$ で割り切れるので $\mu(20)=0$ .

　 $22$ は平方数で割り切れず, $2, 11$ の2つの素因数で構成されるので $\mu(22)=(-1)^2 = 1$ .

$\text{rad}(n)$ ：根基, $n$ の異なる素因数の総積.

　(例) $\text{rad}(20)=\text{rad}(2^2\times 5)= 2\times 5=10$ .

　 $\text{rad}(n)=a+b+c+\dots$ となります.

　今回はこの9種の数論的関数の数表となります.

　某コミュニティなどでmake10するときなどにお使いください.

thetheorier.hatenablog.com

　ピンポイントに調べたい方はこちらをどうぞ.

加法的関数数表

n=1～50

$n$	$\Omega$	$\omega$	$\text{sopf}$	$\text{sopfr}$
1	0	0	0	0
2	1	1	2	2
3	1	1	3	3
4	2	1	2	4
5	1	1	5	5
6	2	2	5	5
7	1	1	7	7
8	3	1	2	6
9	2	1	3	6
10	2	2	7	7
11	1	1	11	11
12	3	2	5	7
13	1	1	13	13
14	2	2	9	9
15	2	2	8	8
16	4	1	2	8
17	1	1	17	17
18	3	2	5	8
19	1	1	19	19
20	3	2	7	9
$n$	$\Omega$	$\omega$	$\text{sopf}$	$\text{sopfr}$
21	2	2	10	10
22	2	2	13	13
23	1	1	23	23
24	4	2	5	9
25	2	1	5	10
26	2	2	15	15
27	3	1	3	9
28	3	2	9	11
29	1	1	29	29
30	3	3	10	10
31	1	1	31	31
32	5	1	2	10
33	2	2	14	14
34	2	2	19	19
35	2	2	12	12
36	4	2	5	10
37	1	1	37	37
38	2	2	21	21
39	2	2	16	16
40	4	2	7	11
$n$	$\Omega$	$\omega$	$\text{sopf}$	$\text{sopfr}$
41	1	1	41	41
42	3	3	12	12
43	1	1	43	43
44	3	2	13	15
45	3	2	8	11
46	2	2	25	25
47	1	1	47	47
48	5	2	5	11
49	2	1	7	14
50	3	2	7	12

n=50～100

$n$	$\Omega$	$\omega$	$\text{sopf}$	$\text{sopfr}$
51	2	2	20	20
52	3	2	15	17
53	1	1	53	53
54	4	2	5	11
55	2	2	16	16
56	4	2	9	13
57	2	2	22	22
58	2	2	31	31
59	1	1	59	59
60	4	3	10	12
61	1	1	61	61
62	2	2	33	33
63	3	2	10	13
64	6	1	2	12
65	2	2	18	18
66	3	3	16	16
67	1	1	67	67
68	3	2	19	21
69	2	2	26	26
70	3	3	14	14
$n$	$\Omega$	$\omega$	$\text{sopf}$	$\text{sopfr}$
71	1	1	71	71
72	5	2	5	12
73	1	1	73	73
74	2	2	39	39
75	3	2	8	13
76	3	2	21	23
77	2	2	18	18
78	3	3	18	18
79	1	1	79	79
80	5	2	7	13
81	4	1	3	12
82	2	2	43	43
83	1	1	83	83
84	4	3	12	14
85	2	2	22	22
86	2	2	45	45
87	2	2	32	32
88	4	2	13	17
89	1	1	89	89
90	4	3	10	13
$n$	$\Omega$	$\omega$	$\text{sopf}$	$\text{sopfr}$
91	2	2	20	20
92	3	2	25	27
93	2	2	34	34
94	2	2	49	49
95	2	2	24	24
96	6	2	5	13
97	1	1	97	97
98	3	2	9	16
99	3	2	14	17
100	4	2	7	14

乗法的関数数表

n=1～50

$n$	$d$	$\sigma$	$\varphi$	$\mu$	$\text{rad}$
1	1	1	1	1	1
2	2	3	1	-1	2
3	2	4	2	-1	3
4	3	7	2	0	2
5	2	6	4	-1	5
6	4	12	2	1	6
7	2	8	6	-1	7
8	4	15	4	0	2
9	3	13	6	0	3
10	4	18	4	1	10
11	2	12	10	-1	11
12	6	28	4	0	6
13	2	14	12	-1	13
14	4	24	6	1	14
15	4	24	8	1	15
16	5	31	8	0	2
17	2	18	16	-1	17
18	6	39	6	0	6
19	2	20	18	-1	19
20	6	42	8	0	10
$n$	$d$	$\sigma$	$\varphi$	$\mu$	$\text{rad}$
21	4	32	12	1	21
22	4	36	10	1	22
23	2	24	22	-1	23
24	8	60	8	0	6
25	3	31	20	0	5
26	4	42	12	1	26
27	4	40	18	0	3
28	6	56	12	0	14
29	2	30	28	-1	29
30	8	72	8	-1	30
31	2	32	30	-1	31
32	6	63	16	0	2
33	4	48	20	1	33
34	4	54	16	1	34
35	4	48	24	1	35
36	9	91	12	0	6
37	2	38	36	-1	37
38	4	60	18	1	38
39	4	56	24	1	39
40	8	90	16	0	10
$n$	$d$	$\sigma$	$\varphi$	$\mu$	$\text{rad}$
41	2	42	40	-1	41
42	8	96	12	-1	42
43	2	44	42	-1	43
44	6	84	20	0	22
45	6	78	24	0	15
46	4	72	22	1	46
47	2	48	46	-1	47
48	10	124	16	0	6
49	3	57	42	0	7
50	6	93	20	0	10

n=50～100

$n$	$d$	$\sigma$	$\varphi$	$\mu$	$\text{rad}$
51	4	72	32	1	51
52	6	98	24	0	26
53	2	54	52	-1	53
54	8	120	18	0	6
55	4	72	40	1	55
56	8	120	24	0	14
57	4	80	36	1	57
58	4	90	28	1	58
59	2	60	58	-1	59
60	12	168	16	0	30
61	2	62	60	-1	61
62	4	96	30	1	62
63	6	104	36	0	21
64	7	127	32	0	2
65	4	84	48	1	65
66	8	144	20	-1	66
67	2	68	66	-1	67
68	6	126	32	0	34
69	4	96	44	1	69
70	8	144	24	-1	70
$n$	$d$	$\sigma$	$\varphi$	$\mu$	$\text{rad}$
71	2	72	70	-1	71
72	12	195	24	0	6
73	2	74	72	-1	73
74	4	114	36	1	74
75	6	124	40	0	15
76	6	140	36	0	38
77	4	96	60	1	77
78	8	168	24	-1	78
79	2	80	78	-1	79
80	10	186	32	0	10
81	5	121	54	0	3
82	4	126	40	1	82
83	2	84	82	-1	83
84	12	224	24	0	42
85	4	108	64	1	85
86	4	132	42	1	86
87	4	120	56	1	87
88	8	180	40	0	22
89	2	90	88	-1	89
90	12	234	24	0	30
$n$	$d$	$\sigma$	$\varphi$	$\mu$	$\text{rad}$
91	4	112	72	1	91
92	6	168	44	0	46
93	4	128	60	1	93
94	4	144	46	1	94
95	4	120	72	1	95
96	12	252	32	0	6
97	2	98	96	-1	97
98	6	171	42	0	14
99	6	156	60	0	33
100	9	217	40	0	10