もう一人のY君

iPhoneアプリのレビューやアップデートレビューなどを書いています. たまに数学の記事も書きます.

もう一人のY君　MENU 　MENU

(数学)空集合上の関数

数学

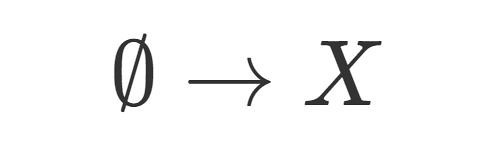
161003_00

　今回は画像の通り, 空集合から任意の集合への関数についてです.

 

[Contents]
 

 

振り返り

thetheorier.hatenablog.com

thetheorier.hatenablog.com

　関数や空集合については以前のエントリで解説しています.

　簡単にこちらでも書いておきましょう.

 

 

[定義：関数]

　集合 { \displaystyle A, B } の順序対 { \displaystyle \langle a, b\rangle } が次を満たすとき, { \displaystyle f } は { \displaystyle A } から { \displaystyle B } への関数と呼びます.

  1. { \displaystyle f } の元はすべて { \displaystyle \langle a, b\rangle } の形であり, かつ { \displaystyle a\in A }, { \displaystyle b\in B } を満たす
  2. { \displaystyle \langle a, b\rangle\in f } かつ { \displaystyle \langle a, c\rangle\in f } ならば, { \displaystyle a=c }
  3. { \displaystyle A } の任意の元 { \displaystyle a } について, { \displaystyle \langle a, b\rangle\in f } となるような { \displaystyle B } の元 { \displaystyle b } が存在する

　そしてこのとき, { \displaystyle b = f(a) } と書き表します.

 

[定義：空集合]

　空集合とは, 任意の集合の部分集合である集合を言う.

 

 

φ上の関数

　では早速 { \displaystyle \emptyset } 上の関数, つまり上記で言うところの { \displaystyle A=\emptyset } の場合を考えてみます.

 

　まず { \displaystyle a\in\emptyset } なる { \displaystyle a } はありませんから, 関数の定義1における「{ \displaystyle \langle a, b \rangle } という形」は存在しません.

　従って { \displaystyle f:\emptyset\to B } なる関数が存在するならば { \displaystyle f=\emptyset } でなければなりません.

 

　逆に { \displaystyle f=\emptyset } ならば, 任意の集合 { \displaystyle B } を取っても関数の定義1～3を満たすのは明らかです.

　空集合でのエントリで使用した論法により, 「矛盾からは任意の命題が導かれる」ので, { \displaystyle \langle a, b\rangle } という形が無くともそこから { \displaystyle a\in\emptyset,\quad b\in B } は導かれますし, また

{ \displaystyle \langle a,b_1\rangle\in f(=\emptyset) \\ \langle a,b_2\rangle\in f(=\emptyset) }

もまた矛盾命題ですからそこから { \displaystyle b_1 =b_2 } が導かれるのも明らかです.

　同様に3つ目も導かれます.

 

スポンサーリンク

 

 

　逆に { \displaystyle f=\emptyset } ならば, { \displaystyle f } の元は存在しないので矛盾命題より関数の定義1がまず満たされます.

　2, 3 についてもそれぞれ

{ \displaystyle \langle a,b_1\rangle\in f\\ \langle a,b_2\rangle\in f }

が矛盾命題であること, そして

{ \displaystyle a\in\emptyset } なる{ \displaystyle a } が存在しない

ことより, それぞれ

{ \displaystyle b_1 = b_2 }
{ \displaystyle \langle a,b\rangle\in f } となるような { \displaystyle b\in B }

 

 

　従って, { \displaystyle \emptyset\to X } なる関数はただ一つ存在して { \displaystyle \emptyset } ということになります.

 

 

〆

　多くの方が, { \displaystyle \emptyset } 上の関数は存在しないと勘違いされているそうです.

　そもそもイメージのしようがありませんので仕方ないかもしれません.

 

 

thetheorier