(数学)平方剰余について - もう一人のY君

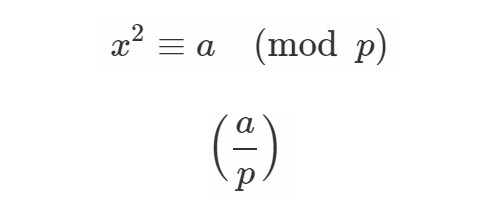
160607_01

　今回は平方剰余のお話です.

　定義云々は今回は簡単に, 本題の方を優先します.

[Contents]

平方剰余とは
- 平方剰余の相互法則
より一般の平方剰余の性質を確かめる
- m=5のとき
- m=7のとき
他の場合
〆
訂正
- 2016.07.31

平方剰余とは

　一般的に, 素数 $p$ について合同式 $x^{n}\equiv a\pmod p$ に解があるか無いか…によって, $a$ を $p$ の $n$ 冪剰余, または非剰余と言います.

　平方剰余では特に $a\neq 0$ , $p$ を奇素数 $(p\neq 2)$ として話を進めます.

　平方剰余は, 合同方程式 $x^{2}\equiv a\pmod p$ が解を持つかどうかに従って

$\Bigl(\frac{a}{p}\Bigr) = +1$ または $-1$

と書き表し, +1のとき平方剰余, -1のとき平方非剰余とします.

　またこの左辺の記号をLegendre(ルジャンドル)の記号と言います.

平方剰余はその定義から, いくつかの性質を持っています.

$x^{2}\equiv (p-x)^{2}\pmod p$ より, $p$ の平方剰余は $1, 2,\dots \frac{p-1}{2}$ の平方である
$a\equiv a'\pmod p$ ならば $\Bigl(\frac{a}{p}\Bigr) = \Bigl(\frac{a'}{p}\Bigr)$
$\Bigl(\frac{abc\dots}{p}\Bigr) = \Bigl(\frac{a}{p}\Bigr)\Bigl(\frac{b}{p}\Bigr)\Bigl(\frac{c}{p}\Bigr)\dots$
$\Bigl(\frac{a}{p}\Bigr)\equiv a^{\frac{p-1}{2}}\pmod p$

　他にもあります.

平方剰余の相互法則

　平方剰余の各種定理でより重要で基本的なものとして, この平方剰余の相互法則があります.

[平方剰余の相互法則]

　 $p, q$ が相異なる奇素数であるとき,

$\Bigl(\frac{p}{q}\Bigr)\Bigl(\frac{q}{p}\Bigr) = (-1)^{\frac{p-1}{2}\frac{q-1}{2}}$

[平方剰余の相互法則第一補充法則]

$\Bigl(\frac{-1}{p}\Bigr) = (-1)^{\frac{p-1}{2}}$

[平方剰余の相互法則第二補充法則]

$\Bigl(\frac{2}{p}\Bigr) = (-1)^{\frac{p^{2}-1}{8}}$

　証明は割愛しますが本題のために意味の解釈を行います.

　まず最初の相互法則ですが, 右辺を見れば分かる通り, 例えば奇素数 $p$ が $p = 4n+1$ という形のとき

$\frac{p-1}{2} \\= \frac{(4n+1)-1}{2} \\ = 2n$

となって偶数となるので全体は 1, そして $p = 4n-1$ のとき

$\frac{p-1}{2} \\= \frac{(4n-1)-1}{2} \\ = 2n-1$

となって奇数となるので全体は-1になります.

　第一補充法則についても同様に $p$ が $4n+1$ という形か $4n-1$ という形か…によって+1, -1になります.

　第二補充法則については $p$ が $8n\pm 1$ か $8n\pm 5$ か…によって+1, -1になります.

　実際確かめてみてください.

より一般の平方剰余の性質を確かめる

　ここからが本題です.

　平方剰余の相互法則により, $\Bigl(\frac{-1}{p}\Bigr)$ や $\Bigl(\frac{2}{p}\Bigr)$ については比較的簡単に求められるのは分かります, ではそれ以外の $\Bigl(\frac{m}{p}\Bigr)$ についてはどうなのか…というわけです.

　平方剰余の性質 $\Bigl(\frac{abc\dots}{p}\Bigr) = \Bigl(\frac{a}{p}\Bigr)\Bigl(\frac{b}{p}\Bigr)\Bigl(\frac{c}{p}\Bigr)\dots$ より, $m$ に相当する部分は素数の場合に限って考えれば十分であることが分かります.

　試しに $m=5$ と $m=7$ について考えてみましょう.

m=5のとき

　まず平方剰余の相互法則により,

$\Bigl(\frac{5}{p}\Bigr)\Bigl(\frac{p}{5}\Bigr) \\= (-1)^{\frac{5-1}{2}\frac{p-1}{2}} \\= (-1)^{p-1} \\ = 1$

となるので, 両辺に $\Bigl(\frac{p}{5}\Bigr)$ をかけて

$\Bigl(\frac{5}{p}\Bigr) = \Bigl(\frac{p}{5}\Bigr)$

となることが分かります.

　つまり $\Bigl(\frac{5}{p}\Bigr)$ を計算するには $\Bigl(\frac{p}{5}\Bigr)$ を評価すれば良いことが分かります.

　はじめに書いた平方剰余の性質

$a\equiv a'\pmod p$ ならば $\Bigl(\frac{a}{p}\Bigr) = \Bigl(\frac{a'}{p}\Bigr)$

から, $m=1, 2, 3, 4$ についてのみ考えれば十分ですね, 順番に計算してみると...

　 $\Bigl(\frac{1}{5}\Bigr)$ は明らかに1です.

　 $\Bigl(\frac{2}{5}\Bigr)$ は第一補充法則から $(-1)^{\frac{5^{2}-1}{8}} = (-1)^{3} = -1$ になります.

　 $\Bigl(\frac{3}{5}\Bigr)$ の前に $\Bigl(\frac{4}{5}\Bigr)$ をやります, これは $\Bigl(\frac{-1}{5}\Bigr)$ のことですから, 第二補充法則から $(-1)^{\frac{5-1}{2}} = (-1)^{2} = 1$ となります.

　 $\Bigl(\frac{3}{5}\Bigr)$ は $\Bigl(\frac{-2}{5}\Bigr)$ ですから, $\Bigl(\frac{-1}{5}\Bigr)$ と $\Bigl(\frac{2}{5}\Bigr)$ の積となります, 従って $1\times -1 = -1$ となります.

　法 $5$ において $4$ は $-1$ , 同様に $3$ は $-2$ と合同ですから, 整理して

$\Bigl(\frac{5}{p}\Bigr) = \Biggl\{ \begin{array} +1\quad (p\equiv\pm 1\pmod 5) \\ -1\quad (p\equiv\pm 2\pmod 5) \end{array}$

であることが分かりました.

m=7のとき

　同じようにまず相互法則より

$\Bigl(\frac{7}{p}\Bigr)\Bigl(\frac{p}{7}\Bigr) \\= (-1)^{\frac{7-1}{2}\frac{p-1}{2}} \\= (-1)^{3\frac{p-1}{2}} \\= (-1)^{\frac{p-1}{2}}$

となるので, 両辺に $\Bigl(\frac{p}{7}\Bigr)$ をかけて

$\Bigl(\frac{7}{p}\Bigr) = (-1)^{\frac{p-1}{2}}\Bigl(\frac{p}{7}\Bigr)$

となることが分かります.

　今回はちょっと面倒そうです.

$(-1)^{\frac{p-1}{2}}$ と $\Bigl(\frac{p}{7}\Bigr)$ の2項あるため, 各々について場合分けして考えます.

　まず前項は平方剰余の相互法則, 第一補充法則の性質と同じ形をしていますから, $p\equiv 1\pmod 4$ のとき $1$ , $p\equiv -1\pmod 4$ のとき $-1$ であることが分かります.

　次項 $\Bigl(\frac{p}{7}\Bigr)$ は $m=5$ の時と同じようにやってみましょう.

　実際に計算すると以下になります.

$\Bigl(\frac{1}{7}\Bigr) = +1$

$\Bigl(\frac{2}{7}\Bigr) = +1$

$\Bigl(\frac{3}{7}\Bigr) = -1$

$\Bigl(\frac{4}{7}\Bigr) = \Bigl(\frac{-3}{7}\Bigr) = +1$

$\Bigl(\frac{5}{7}\Bigr) = \Bigl(\frac{-2}{7}\Bigr) = -1$

$\Bigl(\frac{6}{7}\Bigr) = \Bigl(\frac{-1}{7}\Bigr) = -1$

　実際の結果となる条件はこの2つを満たすものですから, それも計算しておかなければなりません, 例えば $p\equiv 1\pmod 4$ かつ $p\equiv 1\pmod 7$ であるとき, これは $p\equiv 1\pmod {28}$ であることと同値です.

　連立合同式を解く要領でやっていきましょう.

$\pmod 4$	$\pmod 7$	$\pmod {28}$	$(-1)^{\frac{p-1}{2}}$	$\Bigl(\frac{p}{7}\Bigr)$	$\Bigl(\frac{7}{p}\Bigr)$
1	1	1	+1	+1	+1

　あとは上のようにして必要個所を埋めていきます.

　これを $2\times 6=12$ 通りについて計算しておきます.

　実際に埋めると下のようになります.

$\pmod 4$	$\pmod 7$	$\pmod {28}$	$(-1)^{\frac{p-1}{2}}$	$\Bigl(\frac{p}{7}\Bigr)$	$\Bigl(\frac{7}{p}\Bigr)$
1	1	1	+1	+1	+1
1	2	9	+1	+1	+1
1	3	-11	+1	-1	-1
1	-1	13	+1	-1	-1
1	-2	5	+1	-1	-1
1	-3	-3	+1	+1	+1
-1	1	-13	-1	+1	-1
-1	2	-5	-1	+1	-1
-1	3	3	-1	-1	+1
-1	-1	-1	-1	-1	+1
-1	-2	-9	-1	-1	+1
-1	-3	11	-1	+1	-1

　あとは上記太字における関連性を見つけて整理すればOKです, 実際この表により

$\Bigl(\frac{7}{p}\Bigr) = \Biggl\{ \begin{array} +1\quad (|p|\equiv 1, 3, 9\pmod 5) \\ -1\quad (|p|\equiv 5, 11, 13\pmod 5) \end{array}$

であることが分かります(見やすさのため, 表記を変更しました).

他の場合

　この調子でいけば, 理屈としては他の場合でもいくらでも出来ることになります.

　以下に $p=97$ までの場合を紹介します( $p=2$ は相互法則のため除く), 計算間違いがあったら申し訳ないです.

$\Bigl(\frac{3}{p}\Bigr) = \Biggl\{ \begin{array} +1\quad (|p|\equiv 1\pmod {12}) \\ -1\quad (|p|\equiv 5\pmod {12}) \end{array}$

$\Bigl(\frac{5}{p}\Bigr) = \Biggl\{ \begin{array} +1\quad (p\equiv\pm 1\pmod 5) \\ -1\quad (p\equiv\pm 2\pmod 5) \end{array}$

$\Bigl(\frac{7}{p}\Bigr) = \Biggl\{ \begin{array} +1\quad (|p|\equiv 1, 3, 9\pmod 5) \\ -1\quad (|p|\equiv 5, 11\\ \qquad, 13\pmod 5) \end{array}$

$\Bigl(\frac{11}{p}\Bigr) = \Biggl\{ \begin{array} +1\quad (|p|\equiv 1, 3, 5, 7, 9 \\ \qquad, 19\pmod {44}) \\ -1\quad (|p|\equiv 3, 13, 15, 17\\ \qquad, 21\pmod {44}) \end{array}$

$\Bigl(\frac{13}{p}\Bigr) = \Biggl\{ \begin{array} +1\quad (|p|\equiv 1,3,4\pmod {13}) \\ -1\quad (|p|\equiv 2,5\\ \qquad,6\pmod {13}) \end{array}$

$\Bigl(\frac{17}{p}\Bigr) = \Biggl\{ \begin{array} +1\quad (|p|\equiv 1,2,4,8\\ \qquad\pmod {17}) \\ -1\quad (|p|\equiv 3,5,6,7\\ \qquad\pmod {17}) \end{array}$

$\Bigl(\frac{19}{p}\Bigr) = \Biggl\{ \begin{array} +1\quad (|p|\equiv 13,5,9,15,17\\ \qquad,25,27,31\\ \qquad\pmod {76}) \\ -1\quad (|p|\equiv 7,11,13,21\\ \qquad,23,29,33,35,37\\ \qquad\pmod {76}) \end{array}$

$\Bigl(\frac{23}{p}\Bigr) = \Biggl\{ \begin{array} +1\quad (|p|\equiv 1,7,9,11,13,15\\ \qquad,19,25,29,41,43\\ \qquad\pmod {92}) \\ -1\quad (|p|\equiv 3,5,17,21,27\\ \qquad,31,33,35,37,39,45\\ \qquad\pmod {92}) \end{array}$

$\Bigl(\frac{29}{p}\Bigr) = \Biggl\{ \begin{array} +1\quad (|p|\equiv 1,3,5,9,11,13\\ \qquad,17,21,23,31,33,39\\ \qquad,43,51\pmod {116}) \\ -1\quad (|p|\equiv 7,15,19,25\\ \qquad,27,35,37,41,45,47\\ \qquad,49,53,55\pmod {116}) \end{array}$

$\Bigl(\frac{31}{p}\Bigr) = \Biggl\{ \begin{array} +1\quad (|p|\equiv 1,3,5,9,11,15\\ \qquad,23,25,27,33,41,43\\ \qquad,45,49,55\pmod {124}) \\ -1\quad (|p|\equiv 7,13,17,19,21\\ \qquad,29,35,37,39,47,51\\ \qquad,53,57,59\pmod {124}) \end{array}$

$\Bigl(\frac{37}{p}\Bigr) = \Biggl\{ \begin{array} +1\quad (|p|\equiv 1,3,4,7,9,10,11\\ \qquad,12,16\pmod {37}) \\ -1\quad (|p|\equiv 2,5,6,8,13,14\\ \qquad,15,17,18\pmod {37}) \end{array}$

$\Bigl(\frac{41}{p}\Bigr) = \Biggl\{ \begin{array} +1\quad (|p|\equiv 1,2,4,5,8,9,10\\ \qquad,16,18,20\pmod {41}) \\ -1\quad (|p|\equiv 3,6,7,11,12\\ \qquad,13,14,15,17,19\\ \qquad\pmod {41}) \end{array}$

$\Bigl(\frac{43}{p}\Bigr) = \Biggl\{ \begin{array} +1\quad (|p|\equiv 1,3,7,9,13,17\\ \qquad,19,21,25,27,39,41\\ \qquad,49,51,53,55,57,63\\ \qquad,71,75,81\pmod {172}) \\ -1\quad (|p|\equiv 5,11,15,23,29\\ \qquad,31,33,35,37,45,47\\ \qquad,59,61,65,67,69,73\\ \qquad,77,79,83,85\\ \qquad\pmod {172}) \end{array}$

$\Bigl(\frac{47}{p}\Bigr) = \Biggl\{ \begin{array} +1\quad (|p|\equiv 1,9,11,15,17\\ \qquad,19,21,23,25,31,35\\ \qquad,37,39,43,49,53,61\\ \qquad,65,67,81,87,89,91\\ \qquad\pmod {188}) \\ -1\quad (|p|\equiv 3,5,7,13,27\\ \qquad,29,33,41,45,51,55\\ \qquad,57,59,63,69,71,73\\ \qquad,75,77,79,83,85,93\\ \qquad\pmod {188}) \end{array}$

$\Bigl(\frac{53}{p}\Bigr) = \Biggl\{ \begin{array} +1\quad (|p|\equiv 1,4,6,7,9,10\\ \qquad,11,13,15,16,17,24\\ \qquad,25\pmod {53}) \\ -1\quad (|p|\equiv 2,3,5,8,12,14\\ \qquad,18,19,20,21,22,23\\ \qquad\pmod {53}) \end{array}$

$\Bigl(\frac{59}{p}\Bigr) = \Biggl\{ \begin{array} +1\quad (|p|\equiv 1,5,9,11,17,21\\ \qquad,23,25,29,31,39,41\\ \qquad,43,45,47,49,53,55\\ \qquad,57,67,81,83,85,91\\ \qquad,99,103,105,111,115\\ \qquad\pmod {236}) \\ -1\quad (|p|\equiv 3,7,13,15,19\\ \qquad,27,33,35,37,51,61\\ \qquad,63,65,69,71,73,75\\ \qquad,77,79,87,89,93,95\\ \qquad,97,101,107,109,113\\ \qquad,117\pmod {236}) \end{array}$

$\Bigl(\frac{61}{p}\Bigr) = \Biggl\{ \begin{array} +1\quad (|p|\equiv 1,5,7,9,11,13\\ \qquad,23,25,44,47,49,47\\ \qquad,53,63,65,67,71,73\\ \qquad,77,79,81,87,91,93\\ \qquad,95,101,103,105,107\\ \qquad,119\pmod {244}) \\ -1\quad (|p|\equiv 3,15,17,19,21\\ \qquad,27,29,31,35,41,43\\ \qquad,45,49,51,55,57,59\\ \qquad,69,75,83,85,89,97\\ \qquad,99,109,111,113,115\\ \qquad,117,121\pmod {244}) \end{array}$

$\Bigl(\frac{67}{p}\Bigr) = \Biggl\{ \begin{array} +1\quad (|p|\equiv 1,3,7,9,11,17\\ \qquad,21,25,27,29,31,33\\ \qquad,37,43,49,51,63,65\\ \qquad,73,75,77,79,81,87\\ \qquad,89,93,95,99,111\\ \qquad,115,119,121,129\\ \qquad\pmod {268}) \\ -1\quad (|p|\equiv 5,13,15,19,23\\ \qquad,35,39,41,47,53,55\\ \qquad,57,59,61,69,71,83\\ \qquad,85,91,97,101,103\\ \qquad,105,107,109,113\\ \qquad,117,123,125,127\\ \qquad,131,133\pmod {268}) \end{array}$

$\Bigl(\frac{71}{p}\Bigr) = \Biggl\{ \begin{array} +1\quad (|p|\equiv 1,5,7,9,11,23\\ \qquad,25,29,31,35,37,39\\ \qquad,45,47,49,51,55,57\\ \qquad,59,63,67,73,77,81\\ \qquad,99,101,109,115\\ \qquad,121,123,125,127\\ \qquad,129,139\pmod {284}) \\ -1\quad (|p|\equiv 3,13,15,17,19\\ \qquad,21,27,33,41,43,53\\ \qquad,61,65,69,75,79,83\\ \qquad,85,87,91,93,95,97\\ \qquad,103,105,107,111\\ \qquad,113,117,119,131\\ \qquad,133,135,137,141\\ \qquad\pmod {284}) \end{array}$

$\Bigl(\frac{73}{p}\Bigr) = \Biggl\{ \begin{array} +1\quad (|p|\equiv 1,2, 3, 4, 6, 8, 9\\ \qquad, 12, 16, 18, 19,23,24\\ \qquad,25,27,32,35,36\\ \qquad\pmod {73}) \\ -1\quad (|p|\equiv 5,7,10,11,13\\ \qquad,14,15,17,20,21,22\\ \qquad,26,28,29,30,31,33\\ \qquad,34\pmod {73}) \end{array}$

$\Bigl(\frac{79}{p}\Bigr) = \Biggl\{ \begin{array} +1\quad (|p|\equiv 1,3,5,7,9,13\\ \qquad,15,21,25,27,35,39\\ \qquad,43,45,47,49,59,63\\ \qquad,65,71,73,75,81,89\\ \qquad,91,97,101,103,105\\ \qquad,107,117,121,125\\ \qquad,127,129,135,139\\ \qquad,141,147\pmod {316}) \\ -1\quad (|p|\equiv 11,17,19,23\\ \qquad,29,31,33,37,41,51\\ \qquad,53,55,57,61,67,69\\ \qquad,77,83,85,87,93,95\\ \qquad,99,109,111,113\\ \qquad,115,119,123,131\\ \qquad,133,137,143,145\\ \qquad,149,151,153,155\\ \qquad,157\pmod {316}) \end{array}$

$\Bigl(\frac{83}{p}\Bigr) = \Biggl\{ \begin{array} +1\quad (|p|\equiv 1,9,15,17,19,21\\ \qquad,25,29,33,35,37,39\\ \qquad,41,43,47,49,55,61\\ \qquad,65,67,69,71,77,79\\ \qquad,81,91,93,103,109\\ \qquad,113,115,121,135\\ \qquad,139,143,153,155\\ \qquad,159,161,163\\ \qquad\pmod {332}) \\ -1\quad (|p|\equiv 3,5,7,11,13\\ \qquad,23,27,31,45,51,53\\ \qquad,57,59,63,73,75,85\\ \qquad,87,89,95,97,99\\ \qquad,101,105,111,117\\ \qquad,119,123,125,127\\ \qquad,129,131,133\\ \qquad,137,141,145,147\\ \qquad,149,151,157,165\\ \qquad\pmod {332}) \end{array}$

$\Bigl(\frac{89}{p}\Bigr) = \Biggl\{ \begin{array} +1\quad (|p|\equiv 1,2,4,5,8,9,10\\ \qquad,11,16,17,18,20,21\\ \qquad,22,25,32,34,36,39\\ \qquad,40,42,44\pmod {89}) \\ -1\quad (|p|\equiv 3,6,7,12,13\\ \qquad,14,15,19,23,24,26\\ \qquad,27,28,29,30,31,33\\ \qquad,35,37,38,41,43\\ \qquad\pmod {89}) \end{array}$

$\Bigl(\frac{97}{p}\Bigr) = \Biggl\{ \begin{array} +1\quad (|p|\equiv 1,2,3,4,6,8,9\\ \qquad,11,12,16,18,22,24\\ \qquad,25,27,31,32,33\\ \qquad,35,36,43,44,47,48\\ \qquad\pmod {97}) \\ -1\quad (|p|\equiv 5,7,10,13,14\\ \qquad,15,17,19,20,21,23\\ \qquad,26,28,29,30,34,37\\ \qquad,38,39,40,41,42,45\\ \qquad,46\pmod {97}) \end{array}$