もう一人のY君

iPhoneアプリのレビューやアップデートレビューなどを書いています. たまに数学の記事も書きます.

もう一人のY君　MENU 　MENU

【数学】因数分解できるとは

数学

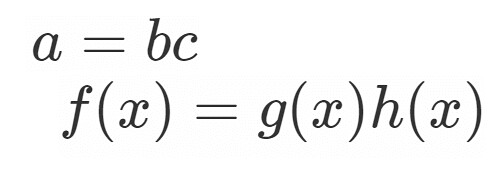
180216_00

　数学において因数分解は基本的であり, かつ重要な考え方の一つですね.

 

スポンサーリンク

 

 

因数分解とは

　その前に因数分解から復習しましょう.

 

　ひとまず数を対象とする集まりで考えます, 具体的には整数 { \displaystyle \mathbb{Z} } の { \displaystyle 0 } でない元 { \displaystyle a } に対して

 

{ \displaystyle a=mn }

 

となる整数 { \displaystyle m,n } が存在するとき, { \displaystyle a } は因数 { \displaystyle m,n } で因数分解できると言い, { \displaystyle m,n } はどちらも { \displaystyle 因数 } と言います.

　特に { \displaystyle m } ないし { \displaystyle n } が素数であるとき, 特別に「素因数」と言い, 任意の正整数は然るべき素因数の積と等しいです, これを「素因数分解」と言います.

 

 

多項式の因数分解

　因数分解は何も数に限ったものではありません.

　例えば多項式でも同様に因数分解の考えができます.

 

　多項式 { \displaystyle f } について,

 

{ \displaystyle f=gh }

 

を満たす整式 { \displaystyle g,h } が存在するとき, { \displaystyle f } は { \displaystyle g,h } で因数分解できると言います.

 

　但し数の因数分解とは違って話は単純ではありません.

 

　例えば { \displaystyle x^4-1 } を因数分解するとしましょう, このときあなたは

 

{ \displaystyle (x^2+1)(x+1)(x-1) }

 

で完結するでしょうか？それとも

 

{ \displaystyle (x+i)(x-i)(x+1)(x-1) }

 

とするでしょうか？

 

　このままではとちらもある意味で正解です, 問題は実数や複素数等, どの範囲で因数分解するべきかの違いです.

 

　後者は虚数である { \displaystyle i } が含まれているため, 例えば「実数の範囲で」因数分解する場合 { \displaystyle x^2+1 } はこれ以上因数分解できないのです.

 

　一般に多項式 { \displaystyle f(x)=a_nx^n+a_{n-1}x^{n-1}+\dots +a_1x+a_0 } は, 最大次数の係数を無視すれば { \displaystyle x+\theta } という形の一次多項式 { \displaystyle n } 個の積で表されます.

 

　このとき { \displaystyle \theta } がどこまで許せるか…で, 因数分解可能な項が変化します, それを考慮すれば { \displaystyle n } 次多項式は「高々」{ \displaystyle n } 個の多項式の積で表せることになります.

 

　従って単に「〜を因数分解してください」では解答が一通りになるとは限りません.

 

 

複素整数

　高校までで学ぶ範囲ではありませんが数の概念の一つとして「複素整数」があります.

　有理整数とは整数のことですが, 初等整数論においてこのように呼ぶことがあります.

 

　有理整数 { \displaystyle a,b } と複素単位 { \displaystyle i } について, 次の数を複素整数, もしくはガウス整数と言います.

 

{ \displaystyle a+bi }

 

　つまり実部虚部ともに整数である複素数をこのように呼ぶわけですね.

 

　複素整数は整数 { \displaystyle \mathbb{Z} } を真に含む環であるため, とくに「ガウス整数環」ともとも言います.

 

 

　整数と似た性質を持ち, 例えば除法の定理

 

{ \displaystyle \beta =\kappa\alpha +\rho ,\, N(\rho)\lt N(\alpha) }

( { \displaystyle N() } はノルムと言い, 複素数の絶対値と同じ定義です )

 

が成り立ちます(但し一意性はありません).

 

 

　また素数に相当する概念もあります.

　複素整数のうち { \displaystyle \pm 1,\, \pm i } の { \displaystyle 4 } つを「単数」と言い, 互いに単数による違いしか無い { \displaystyle 2 } つの複素整数を「同伴」と言うのですが, 単数および { \displaystyle 0 } 以外の複素整数 { \displaystyle \alpha } が単数および同伴数の他に約数を持たないとき, { \displaystyle \alpha } は「有理素数」と言います.

　これが整数(自然数)の素数に当たります.

 

　例えば { \displaystyle 17 } は素数ですが, { \displaystyle 17=(4+i)(4-i) } とできるため有理素数ではありません.

　整数(自然数)の世界では因数分解できない数が, 複素整数の世界だと因数分解できてしまうのですね.

 

thetheorier