もう一人のY君

iPhoneアプリのレビューやアップデートレビューなどを書いています. たまに数学の記事も書きます.

もう一人のY君　MENU 　MENU

【数学】虚数単位のi=√-1は正しいのか？

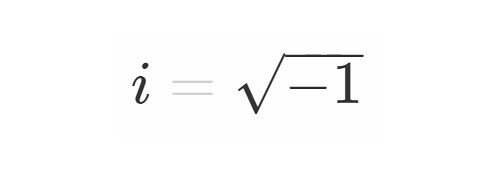
171224_03

　複素数(虚数)を学ぶ上で避けられないのが虚数単位 { \displaystyle i } ですね.

 

 

スポンサーリンク

 

 

虚数単位について

　虚数単位とは

 

「{ \displaystyle -1 }の平方根」
「{ \displaystyle 2 }乗して{ \displaystyle -1 }になる数」

 

などと定義されます.

 

　代数学の言葉で定義すれば, 以下の方程式の根と言えます.

 

{ \displaystyle x^2+1=0 }

 

　しかしこの解は複素数の範囲で二つ存在します, つまり

 

{ \displaystyle \sqrt{-1},\,-\sqrt{-1} }

 

の二つです.

 

　どちらであるべきかは特に決まっておらず, 慣例として前者を採用するのが殆どです, 即ち

 

{ \displaystyle i = \sqrt{-1} }

 

として虚数単位 { \displaystyle i } を定義します.

 

 

内部対称性

　複素数, こと複素単位には面白い性質があり, その一つが内部対称性です.

　複素数でよく知られる性質に複素共役がありますが, 本質的にはそれと同じです.

　つまり任意の複素数 { \displaystyle a+bi } と { \displaystyle a-bi } は共役関係にあります.

 

　この二つの複素数 { \displaystyle a+bi,\,a-bi } は複素数の世界では明確に異なる数であることは間違いないのですが, これが実数の世界になると二つの区別が付かなくなります.

 

　我々がその実在を認めているのは実数まで…という認識である方は多いと思いますが, 過去には負数やゼロですら「存在しないもの」と見なされてきた歴史が(国地域によって)ありました.

　当時の人々にとって, 負数やゼロは存在しない, あり得ないものでした(対して中国など一部では柔軟に受け入れられました).

　それは言うなれば「観測できなかった」訳であり, 現代数学…などとする必要も無く, 現在を生きる我々は(全く解釈が同じであるかは兎も角)当たり前に負数やゼロを扱っています.

 

　つまり我々はそれまで観測できなかった数を観測しているのです.

　ここで言う「観測」は目視という意味ではなく, 数概念として認めている(ないし消極的であっても「否定はしない」)訳です.

 

　教育課程の都合でそれまで「負の平方根は存在しない」と教わり, あるとき突然, 当たり前のように虚数を扱うのを理不尽に感じる方もおられるでしょうが, 文頭の通りでいきなり虚数だなんだと教える訳にもいかない都合があるのでやむを得ません.

　問題なのはその「都合」をあたかも「そこですべて」であると勘違いすること, 或いは講師がそのように教えてしまう事にあるわけですがまぁどんどん本題から逸れてくのでここまでにします.

 

 

n乗根だとどうなる？

　平方根, つまり { \displaystyle2 } 乗根は他に比べ使う頻度が多いため特別扱いされますが(「偶数」なんかもそうですよね), 実際には { \displaystyle 3 }乗根, { \displaystyle 4 }乗根と色々あるわけですね.

 

　実際, 複素数を

 

{ \displaystyle z = r\left(\cos{\theta}+i\sin{\theta}\right) }

 

とすると { \displaystyle z } の { \displaystyle n } 次方程式 { \displaystyle z^n =1 } は複素数の範囲で { \displaystyle n } 個の解を持ちます, 即ち

 

{ \displaystyle \tau_k = r^{\frac{1}{n}}\left(\cos{\frac{\theta +2\pi k}{n}}+i\sin{\frac{\theta +2\pi k}{n}}\right) }
{ \displaystyle \left(k=0,1,2,\dots ,n-1\right) }

 

です.

 

　念の為 { \displaystyle z=-1, n=2 } として { \displaystyle \tau_0 = (-1)^{\frac{1}{2}}, \tau_1 = -(-1)^\frac{1}{2} } となる事を確認してみてください.

 

　各 { \displaystyle \tau_k } は各々が「{ \displaystyle n } 乗して { \displaystyle z } になる数」な訳ですね.

　従ってこの { \displaystyle n } 個のうちどれを「 { \displaystyle n } 乗根」とするか…という問題が発生します.

 

　一番無難なのは { \displaystyle \tau_0 } を採用することです, 即ち

 

{ \displaystyle \tau := \tau_0 }

 

　として { \displaystyle \tau } を「{ \displaystyle z } の { \displaystyle n } 乗根」とする訳ですね.

 

 

〆

　平方根, { \displaystyle 2 }乗根だけ見ると見えてこないものも, 拡張して初めて見えてくるものがあります.

　このような例は他にもたくさんあります.

 

thetheorier