もう一人のY君

主にiPhoneのショートカットアプリのレシピやTipsなどを書いています. たまに数学の記事も書きます.

もう一人のY君　MENU 　MENU

【数学】比率が分からない？

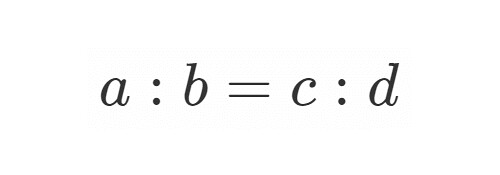
171224_02

　今回は { \displaystyle 1:2=2:4 } と言った比率についての話です.

　比率の「書き換え」の理屈に慣れない方は参考にしてください.

 

スポンサーリンク

 

 

比率とは

　例えば実数 { \displaystyle a,b } について { \displaystyle a:b } とは相対的なもので,

 

{ \displaystyle ad=bc }

 

を満たす実数 { \displaystyle c,d } が存在するとき, { \displaystyle a:b = c:d } という関係を持ちます.

 

　{ \displaystyle b\neq 0, d\neq 0 } とすれば分数や有理数体とも繋がりを持っている事が分かります.

 

　以降は本題のために実数でなく整数として考えることにします.

 

 

文字を使う

　以下では { \displaystyle x:y=2:3 } について考えます, これを { \displaystyle x=}〇, { \displaystyle y= }〇 とするにはどうすれば良いのか…というのが今回の本題です.

 

　先の通りで例えば { \displaystyle x:y=2:3 } は

 

{ \displaystyle 3x=2y \quad \dots (1) }

 

と書きかえられます.

　ある方は (1) から

 

{ \displaystyle x=3k, y=2k }

 

と判断しました, 果たしてこれは正しいでしょうか？

 

 

倍数

　整数 { \displaystyle a,b (b\neq 0) } について, ある整数 { \displaystyle q } が存在して

 

{ \displaystyle a=bq }

 

を満たすとき, 「 { \displaystyle a } は { \displaystyle b } の倍数」と言います.

 

　従って (1) は例えば

 

{ \displaystyle 3x } は { \displaystyle 2 } の倍数

 

が正しい事になります.

 

　然るにある整数 { \displaystyle k' } を用いて

 

{ \displaystyle 3x=2k' }

 

と表せます.

 

　{ \displaystyle 3x } は見ての通り { \displaystyle 3 } と { \displaystyle x } の積であり, 右辺より { \displaystyle 3 } と { \displaystyle x } の何れかは { \displaystyle 2 } の倍数です.

　しかし { \displaystyle 3 } は { \displaystyle 2 } の倍数ではありませんから, { \displaystyle x } が { \displaystyle 2 } の倍数ということになります.

　よってある整数 { \displaystyle k } を用いて

 

{ \displaystyle x=2k }

 

となります.

　これを (1) に代入して整理すれば

 

{ \displaystyle 3x=2y \\ \Leftrightarrow 3\times 2k = 2y \\ \Leftrightarrow y = 3k }

 

となり, { \displaystyle x=2k, y=3k } が正しいことが分かりました.

 

 

〆

　傍目に簡単な事でも, 人に理解してもらえるよう書くのは必ずしも容易ではありません.

　きっかけとなった方はこの説明で納得されましたが万人に納得してもらえる説明であるかはまた別の話です.

 

thetheorier