もう一人のY君

iPhoneアプリのレビューやアップデートレビューなどを書いています. たまに数学の記事も書きます.

もう一人のY君　MENU 　MENU

【数学】割った余りによる分類

数学

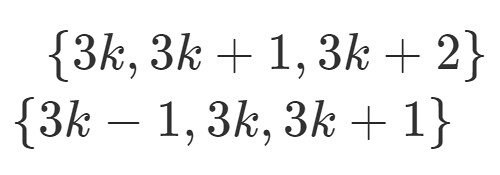
180317_04

　この考え方は合同式に絡みこれまでにも触れてきましたが, 本題に沿って改めて紹介しましょう.

 

スポンサーリンク

 

 

除法の定理

　本題のカギは除法の定理になります.

 

[定理：除法の定理]

　整数 { \displaystyle a,b(b\neq 0) } について,

 

{ \displaystyle a=bq+r }

 

を満たす整数の組 { \displaystyle (q,r), (0\leq r\lt b) } がただ一組存在する.

 

　除法の定理の言わんとする点は, { \displaystyle a } と { \displaystyle b } との関係は勿論のこと, 任意の { \displaystyle a } は { \displaystyle r } 個の

 

{ \displaystyle bq+r }

 

という形で表すことができることを意味しています.

 

　つまり任意の整数 { \displaystyle a } は

 

{ \displaystyle bq, bq+1, bq+2, \dots , bq+r-1 }

 

の何れかで表すことができる, 言いかえれば「分類できる」ことになります.

 

　通常はこれで問題ありません, しかし表記の仕方はこれだけなのでしょうか？

 

 

証明にヒントが

　そのカギは除法の定理の証明法の一つの内容にあります.

　{ \displaystyle b } の倍数を小さい順に並べると

 

{ \displaystyle \dots , -3b, -2b, -b, 0, b, 2b, 3b, \dots }　 …(1)

 

となります.

 

　任意の整数 { \displaystyle a } は上で並べた隣り合う特定の2数の間に必ず存在しますね, つまりある整数 { \displaystyle q } が存在して

 

{ \displaystyle qb\leq a \lt (q+1)b }

 

を満たします.

 

　除法の定理はここから「余り」に相当する数 { \displaystyle r } を指定しますね.

 

 

少し変える

　任意の数 { \displaystyle a } は何も { \displaystyle b } の倍数である必要はありません.

　これを等間隔にズラしたものでも構いません, 従って例えば(1)から整数 { \displaystyle s } だけズラした

 

{ \displaystyle \dots , -3b+s, -2b+s, -b+s, s, b+s, 2b+s, 3b+s, \dots } 　…(2)

 

と { \displaystyle a } の関係を考えても良いはずです.

 

　この(2)を用いれば, 任意の { \displaystyle a } は(2)による隣り合う2数の間に必ず存在します, つまりある整数 { \displaystyle q' } が存在して

 

{ \displaystyle qb+s\leq a \lt (q+1)b+s }

 

を満たします, よって

 

{ \displaystyle r=a-(qb+s) }

 

と { \displaystyle r } を置けば { \displaystyle r } は { \displaystyle 0\leq r\lt b } であり, 上は変形して

 

{ \displaystyle a=qb+r+s }

 

となります.

 

　{ \displaystyle s } は任意でしたから, { \displaystyle a } を表す { \displaystyle r } 個の列

 

{ \displaystyle bq, bq+1, bq+2, \dots , bq+r-1 }

 

は各々を同じ数で足し引きしても問題ないことになります.

 

 

　例えば整数 { \displaystyle a } は整数 { \displaystyle k } を用いて

 

{ \displaystyle 3k, 3k+1, 3k+2 }

 

の何れかで表すことができますが, 例えばこの各々を { \displaystyle 1 } 引いた

 

{ \displaystyle 3k-1, 3k, 3k+1 }

 

でもやはり任意の整数を表すのです.

 

thetheorier