もう一人のY君

iPhoneアプリのレビューやアップデートレビューなどを書いています. たまに数学の記事も書きます.

もう一人のY君　MENU 　MENU

【数学】使用する記号は決まっているのか？【記号一覧】

数学

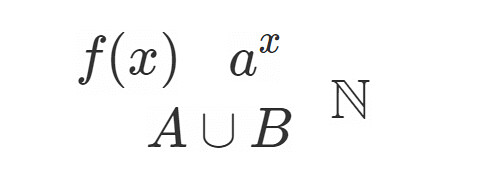
171031_01

　数学では色んな目的で, アルファベットをはじめとする数字以外の様々な記号が用いられています.

 

 

スポンサーリンク

 

 

慣例

　例えば変数は { \displaystyle x } , 関数は { \displaystyle f(x) } …とするのが殆どです.

　これは絶対にそうしなければいけない…というわけではなく,

 

「予めある程度の決まりを断ることで, 後で他の人が見てもその記号の意味を直ぐに理解できる」

 

といった目的であり, それ故慣例としてその使い方を優先しています.

 

　従って例えばテストや試験などでは原則として慣例に従うべきで, そうでない, 例えば自分だけで簡潔する場合はそんな決まりは関係ないので好きにして問題ない事になります.

 

　「自分はこれを使いたい」というのは勝手ですが, それを相手に見せる場合は慣例ではないその使い方を予め断っておくかその場で説明するか, いづれにしろ「それがどういう目的で使われているか」を説明する必要があります.

 

　これは数学に求められるコンピテンシーの一つである「相手に理解してもらう力」にも関わります.

 

　例えばある人が実変数を { \displaystyle z } と置いたとします.

　他の人がそれと知らずに見れば複素数と勘違いするかもしれません.

　それを避ける為に慣例が存在します.

 

　しかし慣例はそこまで強制力を持つものではなく, 同じモノであっても参考書が違えば記号が異なる可能性があります.

　これは各々に従う他ありません.

 

 

慣例一覧

　慣例というのは実際には曖昧なものも含まれており, 国や地域で異なる場合があります.

　それでもある程度共通であろうものの一部を書き留めておきます.

 

　記号に添え字が付き得る場合も含みます.

 

 

A

記号 意味 備考
{ \displaystyle a }  定数   
{ \displaystyle A }  集合   
{ \displaystyle \mathbb{A^k_n} }  アフィン空間   

 

 

B

記号 意味 備考
{ \displaystyle b }  定数  2つ目 
{ \displaystyle B }  集合  2つ目 
{ \displaystyle \mathcal{B} }  ボレル集合   

 

 

C

記号 意味 備考
{ \displaystyle c }  定数  3つ目 
{ \displaystyle C }  集合  3つ目 
{ \displaystyle \mathbb{C} }  複素数   
{ \displaystyle \mathcal{C} }  クラス(類)   

 

 

D

記号 意味 備考
{ \displaystyle d }  定数  4つ目 
{ \displaystyle d }  約数   
{ \displaystyle d }  位数   
{ \displaystyle D }  判別式   

 

 

E

記号 意味 備考
{ \displaystyle e }  ネイピア数   
{ \displaystyle E }  平均(期待値)   

 

 

F

記号 意味 備考
{ \displaystyle f }  関数, 写像   
{ \displaystyle F }  集合  閉集合, 加法族の要素 
{ \displaystyle F }  体   
{ \displaystyle f_X }  確率密度関数   
{ \displaystyle F_X }  分布関数   

 

 

G

記号 意味 備考
{ \displaystyle g }  関数, 写像  2つ目 
{ \displaystyle G }  集合  代数系の空間, 閉集合, 加法族の要素 
{ \displaystyle G }  群   

 

 

I

記号 意味 備考
{ \displaystyle I_A }  定義関数   
{ \displaystyle i }  定数(離散パラメータ)   
{ \displaystyle i }  複素単位   

 

 

J

記号 意味 備考
{ \displaystyle j }  定数(離散パラメータ)  2つ目 

 

 

K

記号 意味 備考
{ \displaystyle k }  定数(離散パラメータ)  3つ目 
{ \displaystyle K }  体  主に多項式環の係数など 

 

 

L

記号 意味 備考
{ \displaystyle l }  直線   
{ \displaystyle L^p }  位相空間(Lp空間)   

 

 

M

記号 意味 備考
{ \displaystyle m }  変数・定数  主に整数 
{ \displaystyle m }  直線  2つ目 

 

 

N

記号 意味 備考
{ \displaystyle n }  変数・定数  主に自然数や整数 
{ \displaystyle n }  定数(離散パラメータ)  主に自然数, 非負整数 
{ \displaystyle \mathbb{N} }  自然数   

 

 

O

記号 意味 備考
{ \displaystyle O }  ランダウの記号   
{ \displaystyle o }  位数(代数学)  参考書によっては { \displaystyle ord } 

 

 

P

記号 意味 備考
{ \displaystyle P }  命題   
{ \displaystyle \mathbb{P} }  無理数   
{ \displaystyle P }  確率   
{ \displaystyle p }  素数   

 

 

Q

記号 意味 備考
{ \displaystyle Q }  命題  2つ目 
{ \displaystyle \mathbb{Q} }  有理数   
{ \displaystyle q }  素数  2つ目 

 

 

R

記号 意味 備考
{ \displaystyle r }  定数・変数  主に円の半径 
{ \displaystyle \mathbb{R} }  実数   
{ \displaystyle R }  環   

 

 

S

記号 意味 備考
{ \displaystyle S }  集合, 空間   

 

 

T

記号 意味 備考
{ \displaystyle t }  定数  主に時間パラメータ 
{ \displaystyle T }  停止時間   

 

 

U

記号 意味 備考
{ \displaystyle U }  (部分)集合   

 

 

V

記号 意味 備考
{ \displaystyle V }  集合(開集合)   
{ \displaystyle V }  分散   

 

 

W

記号 意味 備考
{ \displaystyle w }  複素数   
{ \displaystyle w }  要素(確率論)   

 

 

X

記号 意味 備考
{ \displaystyle X }  空間・集合   
{ \displaystyle X }  不定元   
{ \displaystyle x }  変数   

 

 

Y

記号 意味 備考
{ \displaystyle Y }  集合   
{ \displaystyle Y }  不定元   
{ \displaystyle y }  変数   

 

 

Z

記号 意味 備考
{ \displaystyle Z }  集合   
{ \displaystyle /mathbb{Z} }  整数   
{ \displaystyle z }  変数   

 

 

〆

　これら以外にも使い方はありますし, 中には必ずこういう使い方をしないといけないという決まりもありません.

 

thetheorier