【数学】原始根考察 - もう一人のY君

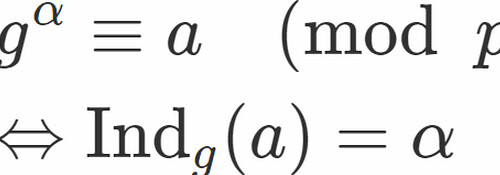
Primitive root inference

　原始根についてのちょっとした推論を見つけました.

　原始根についてはこのブログで何度も登場しました.

　簡単に説明すれば以下になります.

[定義：原始根]

　素数 $p$ と, $p$ で割り切れない整数 $a$ について, $a$ が指数 $p-1$ に対応するとき, つまり $p-1$ よりも小さな正指数で $a^{e}\equiv 1\pmod p$ とならないとき, $a$ を $p$ の原始根と呼ぶ.

　以前紹介した通り, 素数 $p$ における原始根は $\varphi(p-1)$ 個あり, 一つ原始根を見つければ後は芋づる式に見つけることができます.

　しかしこの「与えられた素数からその原始根を任意に一つ求める簡単な方法」は(おそらく)まだ見つかっていません.

　 $g=2,3,4,\dots$ と順に検証するしかないんですね.

　今回はそんな「素数からその原始根を見つけること」ではなく, 素数とその複数ある原始根(3は1つなので除く)についての関係です.

　たまたま昨晩思いついたレベルなのでもっと深い関係があるかもしれません.

　まず5以上の素数とその原始根を小さい順に見てみましょう.

　とりあえず $p=19$ まで書いておきます.

　これを見るだけでははじめは何も思いつかないかもしれません.

　では素数 $p$ における原始根を小さい順に並べたものを $g_1,g_2,\dots,g_{\nu}\,(\nu:=\varphi(p-1))$ とします.

　上の図表から, 素数 $p$ によっては両端沿いに足し合わせると元の素数 $p$ に等しくなることがわかります.

　例えば $p=13$ の場合 $\nu=\varphi(12)=4$ であり,

$g_1+g_4=2+11=13 \\ g_2+g_3=6+7=13$

ですね.

　つまり以下が考えられます.

[推論1]

　任意の $m\in\{1,2,\dots,\nu\}$ について

$p=g_m+g_{\nu-m+1}$

となるような素数 $p$ が存在する.

　しかし例えば $p=11$ の場合は $\nu=\varphi(10)=4$ で,

$g_1+g_4=2+8=10 \\ g_2+g_3=6+7=13$

ということでズレています.

　この $p=13$ のような例は他にも $p=5,17,29,37,41,\dots$ とたくさんあります.

　これらの素数にどのような性質があるでしょうか？

　素数 $p$ の原始根の個数が $\varphi(p-1)$ であることから, $p-1$ に着目すると以下になりました.

$p$	$p-1$	素因数分解	OK?
$5$	$4$	$2^2$	◯
$7$	$6$	$2\cdot3$	×
$11$	$10$	$2\cdot5$	×
$13$	$12$	$2^2\cdot3$	◯
$17$	$16$	$2^4$	◯
$19$	$18$	$2\cdot3^2$	×
$23$	$22$	$2\cdot11$	×
$29$	$28$	$2^2\cdot7$	◯
$31$	$30$	$2\cdot3\cdot5$	×
$37$	$36$	$2^2\cdot3^2$	◯
$41$	$40$	$2^3\cdot5$	◯
$43$	$42$	$2\cdot3\cdot7$	×
$47$	$46$	$2\cdot23$	×

$p$	$p-1$	素因数分解	OK?
$53$	$52$	$2^2\cdot13$	◯
$59$	$58$	$2\cdot29$	×
$61$	$60$	$2^2\cdot3\cdot5$	◯
$67$	$66$	$2\cdot3\cdot11$	×
$71$	$70$	$2\cdot5\cdot7$	×
$73$	$72$	$2^3\cdot3^2$	◯
$79$	$78$	$2\cdot3\cdot13$	×
$83$	$82$	$2\cdot41$	×
$89$	$88$	$2^3\cdot11$	◯
$97$	$96$	$2^5\cdot3$	◯