
ショートカットアプリにある「計算式」アクションでは論理演算が使用できますが, メジャーな演算の一部にしか対応していないのが惜しまれるところです.
ということで既存のアクションを使って基本的な論理演算10種ができる式の例を挙げておきます.
※価格は記事執筆時のものです. 現在の価格はApp Storeから確認ください.
レビュー時のiOSバージョン : iOS15.0
スポンサーリンク
計算式アクションで使える論理演算記号
今の所ショートカットアプリの「計算式」アクションで使える論理演算は
and
xor
or
nor
の4種類です.
andやxorの否定nandおよびnxorなどは使えないため, これら4つ+αで代用しなければなりません.
ただnorは(おそらく)64ビットの端末では2^64に対して行うため必ずしも使いやすいとは限りません.
ビット(バイト)指定できるといいんですけどね.
なお今回はビット演算, つまり0と1に対する演算のみ考えます(論理演算の各アクションは任意の整数に対応しています).
また最後にビット演算の結果を計算する簡単なレシピも紹介しています.
論理積(and)
| 0 | 1 | |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 1 |

論理積andは「計算式」ショートカットで標準で使えるためそのまま
p and q
で問題ありません.
否定論理積(nand)
| 0 | 1 | |
|---|---|---|
| 0 | 1 | 1 |
| 1 | 1 | 0 |

nandは「計算式」では使えないため他の論理演算などを使います.
ビット反転は, 値b(=0or1)に対して
-1×b+1
の通常の演算を行うことで実現できるため, andに対して.
-1(p and q)+1
がnandの代わりになります.
非合意
| 0 | 1 | |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 1 | 0 |

非合意は集合論で言うところのであり, Pが真, Qが偽の場合のみ真となります.
これも「計算式」アクションにないのに加え, 式の組み方も複数通りあるのですが例えば
p xor (p and q)
で求まります.
合意(条件式)
| 0 | 1 | |
|---|---|---|
| 0 | 1 | 1 |
| 1 | 0 | 1 |

集合論ではになります.
こちらも通常の演算でビット反転させた方が速いので
-1(p xor (p and q))+1
とします.
逆非合意
| 0 | 1 | |
|---|---|---|
| 0 | 0 | 1 |
| 1 | 0 | 0 |

集合のに対応します.
p xor (p or q)
で求まります.
逆合意
| 0 | 1 | |
|---|---|---|
| 0 | 1 | 0 |
| 1 | 1 | 1 |

集合のに対応します.
-1(p xor (p or q))+1
で求まります.
排他的論理和(xor)
| 0 | 1 | |
|---|---|---|
| 0 | 0 | 1 |
| 1 | 1 | 0 |

「計算式」アクションに対応し, P,Qの真偽が対の場合のみ真となります.
p xor q
で求めます.
同値(nxor)
| 0 | 1 | |
|---|---|---|
| 0 | 1 | 0 |
| 1 | 0 | 1 |

xnorは「計算式」アクションで使えないため, xorと反転を使って
-1(p xor q)+1
で代用します.
論理和(or)
| 0 | 1 | |
|---|---|---|
| 0 | 0 | 1 |
| 1 | 1 | 1 |

論理和orは「計算式」アクションで使用可能なので, そのまま
p or q
とします.
否定論理和(nor)
| 0 | 1 | |
|---|---|---|
| 0 | 1 | 0 |
| 1 | 0 | 0 |

否定論理和norはショートカットで使える論理演算なのですが, 64ビット(32ビット端末の場合はおそらく32ビット)に対して演算されるため, ビット演算として使うと18442...という20桁の数になってしまいます.
これを補完するために結果からを引き,
(p or q)-(2^(64)-2)
とします.
(補足:ビット演算レシピ)
画像で紹介したような, 式の組み合わせに対応する真理値を返すレシピです.
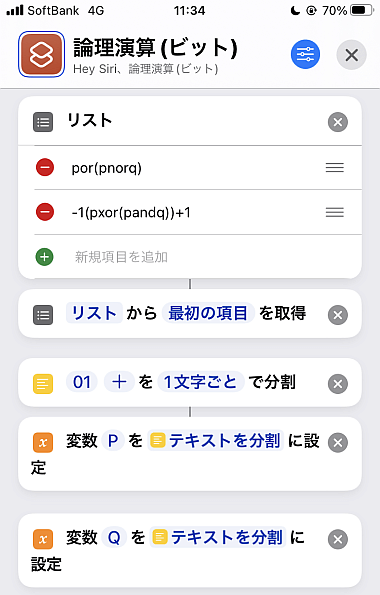
先頭においた「リスト」アクションに好きな論理式を書き, 先頭に置いたものを対象に処理する内容にしてあります.
2つの命題を半角アルファベットp,qで書くと約束します.
リストの最初の項目を取得しておき, 01という文字列を分割してその列をP,Qの変数で置きます.
このPとQはどちらも0と1のリストということになります.

0と1のリストに対して「各項目を繰り返す」を行うことで0,1の4つの組み合わせに対応します.
Pの繰り返しインデックスの項目, Qの繰り返しインデックスの項目を取り出し, それぞれ変数p,qで置きます.

レシピの初めにリストから取り出した最初の項目に対して文字pおよびqをそれぞれ上で得た変数pおよびqに置き換えます.
これでp,qの箇所が繰り返しに応じて0または1に置き換わるのでこれをそのまま「計算式」に代入します.
あとは「テキスト」アクションで体裁を整え, 好きな変数に追加します.
繰り返しが終わったら追加した変数を表示されて完了です.
〆
iOS15になってnxorだったり底を指定できる対数だったりが追加されてるかと期待したんですが残念ながらダメなようです.
論理演算は使用する演算子によって同値となる式があります.
ここで紹介したものが一通りでないので色々試してください.


