もう一人のY君

iPhoneアプリのレビューやアップデートレビューなどを書いています. たまに数学の記事も書きます.

もう一人のY君　MENU 　MENU

【数学】「定義域」には2通りの意味がある？

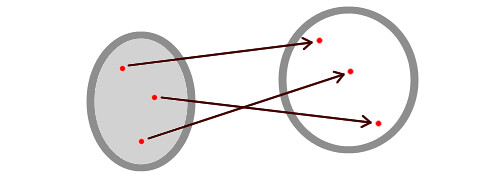
180317_02

　数学における基本的な道具の一つである関数に必ず関わってくるものの一つが定義域ですね.

 

スポンサーリンク

 

 

復習

　このブログでも何度か紹介していますが改めて定義に触れましょう.

 

[定義：関数]

　集合 { \displaystyle A,B } について, { \displaystyle f} が { \displaystyle A } から { \displaystyle B } への関数であるとは, 以下の条件を満たすことを言います.

 

  1. { \displaystyle f } の任意の元はすべて { \displaystyle　\langle a,b\rangle } の形である { \displaystyle (a\in A, b\in B) }
  2. { \displaystyle \langle a,b\rangle\in f, \langle a,c\rangle\in f } ならば { \displaystyle b=c }
  3. { \displaystyle A } 任意の元 { \displaystyle a } について, { \displaystyle \langle a,b\rangle\in f } を満たすような { \displaystyle b\in B } が存在する

 

　このとき, { \displaystyle f:A\to B } と書き表し, また { \displaystyle b } を { \displaystyle f(a) } と書き表せば

 

{ \displaystyle \langle a,b\rangle\in f \Leftrightarrow b=f(a) }

 

が成り立ち, 関数を使う上で順序対は必ずしも不要であることが分かります.

 

　更にこのとき { \displaystyle A } を始域(domain), { \displaystyle B } を終域(codomain)と呼びます.

 

　また"定義域"を指定せず「関数 { \displaystyle f } 」とした場合は { \displaystyle f:\mathbb{R}\to\mathbb{R} } と解釈するのが一般的です.

 

 

2つの定義域

　では本題に入ります.

　気付く方もおられるでしょうが上の「始域」が定義域ではないのか？と思うでしょう.

 

 

一つ目の定義域

　実際始域と定義域を同一視する解釈もありますが後者はもう一つの解釈があるのです.

 

　まず一つ目の定義は始域と同じものです, 言ってみれば「値」が定まるような元をすべて集めた集合ですね, 従って

 

{ \displaystyle \text{Dom}(f) := \{ a\in A | f(a)\in B \} }

 

とも表現できます.

 

　最初に書いた { \displaystyle A } は { \displaystyle f(a) } が { \displaystyle B } の元として必ず存在するように, つまり

 

{ \displaystyle A = \text{Dom}(f) }

 

を満たしているとも言えます.

 

 

二つ目の定義域

　二つ目はその部分集合の場合です.

　つまり { \displaystyle A_0\subseteq A=\text{Dom}(f) } となる集合 { \displaystyle A_0 } における

 

{ \displaystyle f_{A_0} = \{ \langle a,b\rangle | a\in A_0 , f(a)\in B \} }
{ \displaystyle f:A_0\to B }

 

という関数を考えることになります.

　このとき { \displaystyle B } はその真部分集合で済む可能性もあることは言うまでもありません.

 

　このように「一部を切り取る」ことは特に珍しい事ではなく, 分かりやすい例は三角関数でしょうかね.

 

　三角関数は { \displaystyle f:\mathbb{R}\to [0,1] } な関数ですが, しばしば定義域を { \displaystyle [0,2\pi] } などに制限しますよね.

 

　またここにおいて「関数」と言われたら問答無用で { \displaystyle \mathbb{R}\to\mathbb{R} } であると限らないことにも気づきます.

　その数式が定める関数における定義域および値域が共に { \displaystyle \mathbb{R} } であるかどうかは, 数式自身あるいは目的に応じてその少なくとも一方が真部分集合であり得るのです.

 

 

定義域と書かれていたら？

　結局のところ, { \displaystyle \text{Dom}(f) } は言うまでもなく, その真部分集合もまた定義域と呼んでいることになります.

　従って

 

定義域と書かれていてもそれが { \displaystyle \text{Dom}(f) } であるとは限らない

 

ということになります.

 

　「定義域を〜とする」としている場合は真部分集合である可能性があると思わせてそうとも限りませんし, できることはその場その場で見極めるしかありません.

　とは言えこの違いで困ることは殆ど無いでしょう, 定義域が指定されているならばそれに従い, 特に触れていなければ { \displaystyle \text{Dom}(f) } と解釈するのが自然だと思います.

 

　…と言いつつ, 明らかに { \displaystyle [0,\infty)\subset \mathbb{R} } や { \displaystyle (0,\infty)\subset\mathbb{R} } である { \displaystyle \sqrt{x} } や { \displaystyle \log{x} } について, 定義域が書かれていないからと言って { \displaystyle f:\mathbb{R}\to\mathbb{R} } とすることはないでしょう.

　この辺は各々の関数毎で臨機応変に対応することになります.

 

 

まとめ

　つまるところ, 上で挙げた集合

 

  • 始域 { \displaystyle A }
  • 定義域1 { \displaystyle \text{Dom}(f) }
  • 定義域2 { \displaystyle D }

 

について次のような関係が成り立ちます.

 

{ \displaystyle D\subseteq \text{Dom}(f) = A }

 

　解釈次第では定義域と始域の関係は

 

  • 始域の部分集合が定義域
  • もっとも大きい定義域が始域

 

と言えます.

 

thetheorier