もう一人のY君

主にiPhoneのショートカットアプリのレシピやTipsなどを書いています. たまに数学の記事も書きます.

もう一人のY君　MENU 　MENU

【数学】加法族と測度

数学

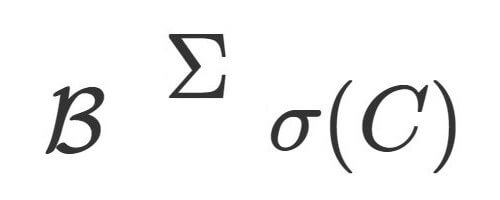
160919_02

　今回は数学の中でも測度論の基礎である加法族, そして測度のお話.

　以降のエントリのために, タイトルに+αな内容もあります.

 

スポンサーリンク

 
[Contents]
 

 

測度論とは

thetheorier.hatenablog.com

　先日紹介した位相空間然り, 数学という世界は原則として議論する対象の集まりを定め(「空間」), それに演算や順序, 位相などの「構造」をくっつけたものになります.

　普段当たり前に考えているそれは既に知っているこれらを当たり前に使用していますが, 数学ではこういった構造そのものも議論の対象になります.

 

　今回の測度論は, その特徴が位相空間によく似ています.

　位相空間は開集合の集まりに関する理論であり, その解釈の一つとして「関数 { \displaystyle f } が連続である」ということを

開集合 { \displaystyle G } の, { \displaystyle f } による逆像 { \displaystyle f^{-1}(G) } が開集合である

として特徴づけますが.

　一方測度論は可測集合の集まりに関する理論であり, その解釈の一つとして「関数 { \displaystyle f } が連続である」ことを

可測集合 { \displaystyle F } の, { \displaystyle f } による逆像 { \displaystyle f^{-1}(F) } が可測集合である

として特徴づけます.

 

　また位相空間では先日の通り開集合の概念が公理化され, 具体的には

  1. 開集合の任意の集まりの和は開集合
  2. 開集合の有限個の共通集合は開集合

であることが求められます.

　対して測度論では可測集合の概念が公理化され, 具体的には

  1. 可測集合の可算個の和は可測集合
  2. 可測集合の有限個の共通集合は可測集合

であることが求められます.

　こうして見ると, どちらかというと閉集合の公理の方が近いですね.

 

 

スポンサーリンク

 

加法族

　ではまず加法族からです.

　因みに「族(=family)」と先程の「系」は共に「集合の集まり」を意味します.

　「集合の集合」と言うわけにはいきませんからね…

　違いは, その後写像を想定するかどうか…という感じですかね.

 

[定義：加法族]

　集合 { \displaystyle S } の部分集合による集まり(系) { \displaystyle \Sigma_{0} } が { \displaystyle S } 上の加法族であるとは, 以下を満たすものである.

  1. { \displaystyle S\in\Sigma_{0} }
  2. { \displaystyle F\in\Sigma_{0}\quad\Rightarrow F^{c}:=S\backslash F\in\Sigma_{0} }
  3. { \displaystyle F,G\in\Sigma_{0} \quad\Rightarrow F\cup G\in\Sigma_{0} }

　パッと見位相空間の公理などと変わらないですよね.

　また上記1と3は2によりそれぞれ

{ \displaystyle \emptyset\in\Sigma_0 }
 { \displaystyle F,G\in\Sigma_{0}\quad\Rightarrow F\cap G\in\Sigma_{0} }

に差し替えても問題無いですね.

(上記で { \displaystyle S\in\Sigma_0 } としていましたが { \displaystyle \emptyset\in\Sigma_0 } の間違いでした, 失礼しました)

 

 

σ-加法族

　加法族には, 更に先のσ-加法族という族があります.

　σ-algebraや完全加法族と言ったりもします.

　どう呼ぶかは参考書次第.

 

[定義：σ-加法族]

　集合 { \displaystyle S } の部分集合系 { \displaystyle \Sigma } は { \displaystyle S } 上の加法族であり, かつ { \displaystyle F_n\in\Sigma (n\in\mathbb{N}) } に関して常に

{ \displaystyle \bigcup_{n\in\mathbb{N}} F_n\in\Sigma }

が成り立つとき, { \displaystyle S } 上のσ-加法族と言う.

 

　位相空間と同じく, 空間 { \displaystyle S } 次第ではσ-加法族の要素を具体的に書き下すのは難しいでしょう.

 

 

可測空間

[定義：可測空間]

　集合 { \displaystyle S } 上の部分集合系 { \displaystyle \Sigma } が { \displaystyle S } 上のσ-加法族であるとき, 対 { \displaystyle (S, \Sigma) } を可測空間と呼ぶ.

　このとき { \displaystyle \Sigma } の要素は { \displaystyle S } の { \displaystyle \Sigma - }可測な部分集合, 或いは簡単に可測集合と言う.

 

　これで取り敢えず可測集合の話まで来ました.

 

 

部分集合の類(クラス)によって生成されるσ-加法族

　指定した集合の集まり(類) { \displaystyle \mathcal{C} } を用いて可測空間, ひいては後述する測度空間の下で議論を行うためには, なんとかしてそれを含むσ-加法族を作る必要があります.

　その類を含むσ-加法族はいくらでも考えられます, その中で一番都合がよいのは「その類を含む最小のσ-加法族」でしょう.

　こうして作ったσ-加法族を { \displaystyle \mathcal{C} } によって生成されるσ-加法族と言います.

　言いかえれば { \displaystyle \Sigma } は { \displaystyle S } 上のσ-加法族であり, かつ { \displaystyle \mathcal{C}\subset\Sigma } を満たす最小のものを言います.

 

 

類(クラス)とは

　これも系や族と似たようなもので, 対象の集まりであることには変わりませんが, こちらは「対象の集まりであって, かつそれに属するすべての要素(元)がもれなく定義されている」ことが要請されます.

　集合の表記法で, 要素を具体的に書きならべる外延的記法と, その要素が属する性質によって集合を表す内包的記法がありますが, この後者の解釈とも言えます.

 

　またある解釈では, 類は「その対象の集まりの部分集合を議論することを想定しない」というのもあるようです.

　現に上記では飽くまでも生成元として例示しています.

 

　一般的な数学では, 集合や系, 族, 類に関して明確に意味分けする機会はあまり無いでしょう.

　集合論ならではとも言えます(理解するのが難しいってのも…).

 

 

ボレルσ-加法族

　σ-加法族で一番扱うものの一つはこのボレルσ-加法族でしょう.

 

[定義：ボレルσ-加法族]

　集合 { \displaystyle S } の開集合全体による集合族によって生成されるσ-加法族をボレルσ-加法族と言う.

 

　特に, { \displaystyle S = \mathbb{R} }, つまり実数集合の場合がよく使われ, しばしば

{ \displaystyle \mathcal{B} := \mathcal{B}(\mathbb{R}) }

と略記されます.

 

 

集合関数の加法性・可算加法性

　続いて, 加法族(σ-加法族)による関数について定義します.

 

[定義：加法性]

　集合 { \displaystyle S } と, その上の加法族 { \displaystyle \Sigma_{0} } について, { \displaystyle \mu_{0} } を非負集合関数とする.

{ \displaystyle \mu_{0} : \Sigma_{0}\to [0, \infty] }

　このとき, { \displaystyle \mu_{0} } が加法的であるとは, 以下を満たすことを言う.

  1. { \displaystyle \mu_{0}(\emptyset) = 0 }
  2. { \displaystyle F,G\in\Sigma_{0} } に対して { \displaystyle F\cap G=\emptyset\quad \\ \Rightarrow\quad\mu_{0}(F\cup G)=\mu_{0}(F)+\mu_{0}(G) }

 

 

[定義：可算加法性]

　集合関数 { \displaystyle \mu_0 : \Sigma_0\to[0,\infty] } は, { \displaystyle \mu(\emptyset)=0 } で, { \displaystyle \Sigma_0 } の要素列{ \displaystyle (F_n : n\in\mathbb{N}) } について, { \displaystyle F = \bigcup F_n } が { \displaystyle \Sigma_{0} } の要素であるとき常に

{ \displaystyle \mu_{0}(F) = \sum_{n}\mu_{0}(F_n) }

が成り立つとき, 可算加法的であると言う.

　ここで, { \displaystyle \Sigma_{0} } はσ-加法族であることを要請していない点が注意です.

 

 

測度と測度空間

[定義：測度空間]

　{ \displaystyle (S,\Sigma) } を可測空間とする.

　写像

{ \displaystyle \mu : \Sigma\to[0,\infty] }

が可算加法的であるとき, { \displaystyle \mu } は { \displaystyle (S,\Sigma) } 上の測度であると言う.

　また三つ組 { \displaystyle (S,\Sigma,\mu) } を測度空間と言う.

　測度空間は言うまでも無く測度, つまり「長さ」に関する空間を厳密化したものです.

 

　特に { \displaystyle \mu(S)=1 } であるとき, { \displaystyle \mu } は確率測度と呼ばれ, { \displaystyle (S,\Sigma,\mu) } を確率三つ組と呼びます.

　そう, 測度は確率論とも繋がっているのです.

 

　それまではくじやギャンブルといったイメージでしか無かった確率論がこの測度論によって明確に公理化され, 結果的に金融や保険関連で日の目を浴び, 今に至っています.

 

 

〆

　今回は定義ばかりでした.

　次回はこれらを使った定理を一つ紹介したいと思います.

 

 

thetheorier