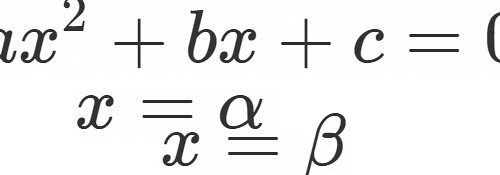
二次方程式に関する問題に関わっていれば嫌でも経験された事でしょう.
スポンサーリンク
「2つある」ということ
(実数係数)二次方程式に実数解が高々二つあることは周知の通りです.
- (異なる)実数解が2つ
- 実数解が1つ(重解)
- 実数解が無い(虚数解)
「実数解が二つ」の解釈
問題によってはしばしば「実数解が二つ」と表現します.
これが解答者を迷わせる原因となっています, つまり「重解の解釈」であり,
- どちらも等しくかつ同じであるから「1つ」
と, 2項の積なのだから「2つ」
, 解釈の仕方は様々でしょうがいづれも妥当に見えます.
どちらが正しいか
「解を二つ持つ」と表現したときにどちらであるか, それを決める慣例は(どうやら)特に無く, また問題によってはどちらの解釈もあるようです.
個人的には「一つ」であろうと思いますが他方も棄てきれない.
一意であるべき, 演繹であるべき数学が, 意外にも曖昧であるのはそれ自体が我々をモヤモヤさせますが, 過去に紹介した箱ひげ図然り, 数学には意外と曖昧性が顔を覗かせます.
誤解を招く表記はしない
しばしば話題になる「」がそうであるように, 解答者次第で解釈が変わり, 果ては答えまで変わってしまうような問題は問題として不適切であると言う他ありません.
出題者は, どんな人であっても, その分野に理解ある者であれば必ず一通りに解釈でき, 一通りの解答に至るようにしなければなりません.
これは数学に求められるコンピテンシーの一つであり, つまり「表現力」が欠如していると言わざるをえません.
その要因は必要な言葉の省略によるものであったり, 2通り以上に解釈できるような曖昧な表現であったり様々です.
数学は, 思いの外「国語力」が求められます.
計算だけで済むそれは数学という世界のほんの一握りに過ぎません.
中央教育審議会 初等中等教育分科会 教育課程部会 教育課程企画特別部会(第15回)配付資料 [資料2] OECDにおける「キー・コンピテンシー」について−文部科学省こうしたなか、OECDはプログラム「コンピテンシーの定義と選択」(DeSeCo)を1997年末にスタート。(2003年に最終報告。PISA調査の概念枠組みの基本となっている。)
キー・コンピテンシーとしての数学は, どれだけ学生に, そして講師に影響を与えたのかは, とっくに学生から卒業し, また講師以外の道を歩いている僕には詳しくは知りませんが, いずれにしろ数学, いや数学以外でも, 「受験○○」といった教育がなされていないはず…と思いたいものです.
