もう一人のY君

iPhoneアプリのレビューやアップデートレビューなどを書いています. たまに数学の記事も書きます.

もう一人のY君　MENU 　MENU

0は倍数かどうか

数学

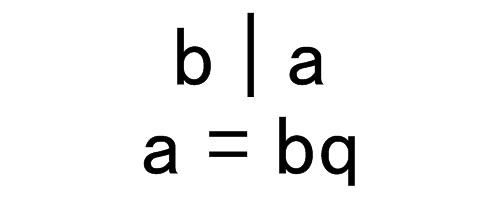
 160412_00

　ちょくちょく議論になるお話ですね.

 

[Contents]
 

 

0は倍数でないのか

　質問サイトをはじめ, よくこんな事を言われます.

　「0は自然数じゃないから倍数じゃない」「0はいくらかけても0だから倍数じゃない」, 「じゃない派」の主張の多くはこの2つのようです.

　では果たしてこれは正しいでしょうか？

　ウィキペディアみれば一発でつまらないのでもうちょっとだけ掘り下げます.

 

 

学んだ時点か, その先か

　結論から言うと「強ち間違ってはいない」です.

　数学で重要なことは, 「どんな空間のもとで議論しているか」です, これは重要というより必要最低限の話です.

　従って自然数, 誤解のないよう書くならば「正の整数」のもとでの話ならばこれは正しいです.

　特に高校数学まででは倍数などの話をするときは自然数とすることが多いです.

　従って理解の仕方によっては「学校でそう教わったんだから倍数は自然数だけだ」と思い込んでいる可能性があります.

 

 

参考書の見解

　ちょっと古いですが以前簡単に調べたことがあったのでそれを改めて取り上げましょう(以下一部引用, 敬称略).

　各々で0がいずれかの倍数なのかについて結構分かれているのが分かると思います.

(前後の重版の違いによって内容が一部異なる可能性がゼロではないことをご了承ください)

 

 

1 : 岩波書店「数論入門」山本芳彦
数論入門 (現代数学への入門)
posted with カエレバ
山本 芳彦 岩波書店 2003-11-11
Amazon
楽天市場
 

 (倍数・約数の定義)

　2つの整数 { \displaystyle m, a } について, { \displaystyle m = ab } となるような整数 { \displaystyle b } が存在するとき, { \displaystyle m } は { \displaystyle a } の倍数であり, { \displaystyle a } は { \displaystyle m } の約数である. (p.7)

(その他)

　0の倍数は0のみである. { \displaystyle a\neq 0 } のときには, { \displaystyle a } の倍数は無限にあって,

{ \displaystyle \mathbb{Z}a = \{na | n\in \mathbb{Z}\} }

と表すことができる. (p7)

(考察)

　山本氏は当著書で「0の倍数は0のみ」と主張していますね.

　倍数が無限にあるのは { \displaystyle a\in 0 } なる整数 { \displaystyle a } に限っています.

　ここで「自然数」でなく「整数{ \displaystyle \mathbb{Z} }」としていることもポイントです.

 

 

2 : 森北出版株式会社「初等代数学」硲文夫
初等代数学 (新数学入門シリーズ)
posted with カエレバ
硲 文夫 森北出版 1993-11
Amazon
楽天市場
 

(倍数・約数の定義)

　整数 { \displaystyle a, b } が与えられているとする. もし, { \displaystyle a = qd } となるような整数 { \displaystyle q } があるならば, { \displaystyle d } は { \displaystyle a } の約数である. あるいはまた, { \displaystyle a } は { \displaystyle d } の倍数である. (p.9) 

(考察)

　こちらではこれ以上触れられていないと思われます.

　しかしこの定義に従えば { \displaystyle a = 0 } とすることで「{ \displaystyle 0 } は { \displaystyle d } の倍数」であると主張できます.

 

 

3 : 朝倉書店「数 - 体系と歴史」足立恒雄
数―体系と歴史
posted with カエレバ
足立 恒雄 朝倉書店 2002-01
Amazon
楽天市場

(倍数・約数の定義)

　整数 { \displaystyle a, b } に対して, { \displaystyle b = ca } を満たす整数 { \displaystyle c } が存在するとき, { \displaystyle b } は { \displaystyle a } の倍数であるといい, { \displaystyle a } は { \displaystyle b } の約数であるという. 記号では { \displaystyle a|b } と表す. (p.100)

(その他)

　{ \displaystyle 0 } はすべての整数の公倍数である. また { \displaystyle \pm 1 } はすべての整数の公約数である. (p.100)

(考察)

　{ \displaystyle 0 } はすべての整数の公倍数ということは, すべての整数の倍数ということですね.

 

 

4 : ベレ出版「数と計算の意味がわかる」野崎昭弘, 何森仁, 伊藤潤一, 小沢健一
数と計算の意味がわかる―数学の風景が見える
posted with カエレバ
野崎 昭弘,伊藤 潤一,何森 仁,小沢 健一 ベレ出版 2001-02
売り上げランキング : 250270
Amazon
楽天市場
 

(倍数・約数の定義)

　記述なし.

(その他)

　すべての数の倍数とも言える( { \displaystyle a\times 0 = 0 } より). (p.32)

(考察)

　サクッとしたまとめのような記述でしたがされてはいたので触れました.

 

 

5 : 丸善株式会社「数の理論 入門」関沢正躬
数の理論 入門
posted with カエレバ
関沢 正躬 丸善 2004-11
Amazon
楽天市場
 

(倍数・約数の定義)

　自然数 { \displaystyle a } に対して, { \displaystyle a } を割りきる自然数を { \displaystyle a } の約数という. 自然数 { \displaystyle a } が自然数 { \displaystyle p } と { \displaystyle q } により { \displaystyle a = pq } と表されるとき, { \displaystyle p } は { \displaystyle a } の約数であり, さらに { \displaystyle p\neq a } であれば { \displaystyle q } も { \displaystyle a } の約数である. (p.11)

　自然数 { \displaystyle p } に自然数をかけてできる数を { \displaystyle p } の倍数という. つまり, 自然数 { \displaystyle p } と { \displaystyle q } に対して { \displaystyle p・q = a } であるとき, { \displaystyle a } は { \displaystyle p } の倍数である. このとき, ( { \displaystyle p\neq q } であれば) { \displaystyle a } は { \displaystyle q } の倍数でもある. (p.22)

(その他)

　またどんな自然数に { \displaystyle 0 } をかけても { \displaystyle 0 } になるから { \displaystyle 0 } はすべての自然数の倍数である. (p.22)

(考察)

　3項目目でハッキリと「0はすべての自然数の倍数である」と論じています.

　2項目目が釈然としませんけどね, { \displaystyle 2\times 2 = 4 } で4は2の倍数だと思うんですけどわざわざ { \displaystyle p\neq q } とする意味はあるんでしょうか…

　またこの書籍では「自然数」の上で論じていますね.

 

 

6 : 日本評論社「数を数えてみよう」中島匠一
数を数えてみよう (はじめよう数学)
posted with カエレバ
中島 匠一 日本評論社 2004-07
Amazon
楽天市場
 

(倍数・約数の定義)

　2つの整数 { \displaystyle a, b } があるとき「 { \displaystyle b } を { \displaystyle a } で割った商と余りを求める」操作ができる. ただし, { \displaystyle 0 } で割ることはできないので { \displaystyle a\neq 0 } とする. また, { \displaystyle a } が負であれば { \displaystyle a } で割る代わりに { \displaystyle -a } で割ればよいので, { \displaystyle a\geq 1 } として考える. ～中略～

{ \displaystyle b = qa } ( { \displaystyle q } は整数)

であるとき, 「{ \displaystyle a } は { \displaystyle b } の約数(divisor)である」とか「{ \displaystyle b } は { \displaystyle a } の倍数(multiple)である」などという. (p.7)

(その他)

　0でない整数の約数は有限個しかないから, { \displaystyle a = b = 0 } という"極端な場合"を除いておけば, { \displaystyle a } と { \displaystyle b } の公約数は有限個しかない. (p.7)

(考察)

　こちらでも「0は～～の倍数」を想定した記述になっているのが分かります.

 

 

7 : 朝倉書店「ゼロからわかる数学 -数論とその応用-」戸部美郎
シリーズ 数学の世界 1 ゼロからわかる数学数論とその応用
posted with カエレバ
戸川 美郎 朝倉書店 2001-06
売り上げランキング : 544339
Amazon
楽天市場
 

(倍数・約数の定義)

　「割り切れるとき」を「整数 { \displaystyle a, b } がどのような条件を満たすとき, 方程式 { \displaystyle ax = b } の(整数)解が存在するか？」と言える. (p.22, 以下断りがないかぎり同ページ)

　{ \displaystyle b = 0 } のとき, このときは, { \displaystyle a } が何であっても, 解は存在する( { \displaystyle x = 0 } とすればよい).

　{ \displaystyle a = 0 } のときは, { \displaystyle b } も0でない限り解は存在しない.

　{ \displaystyle a = 1 } のときは, いつでも解が存在する( { \displaystyle x = b } とすればよい).

　整数 { \displaystyle b } が整数 { \displaystyle a } の倍数であることは, { \displaystyle b = ax_{0} } を満たす整数 { \displaystyle x_{0} } が存在するときである.

(その他)

　どのような(0でない)整数 { \displaystyle b } に対しても, { \displaystyle 1, b, -1, -b } はいつでも { \displaystyle b } の約数になる. このような約数を自明な約数ということにしよう. (p.23)

　「 { \displaystyle b } が { \displaystyle a } で割り切れる」こと, 「 { \displaystyle b } が { \displaystyle a } の倍数である」こと, 「 { \displaystyle a } が { \displaystyle b } の約数である」ことは結局, 同じことである. ただし, 「0は0の倍数である」ということはよいのだが, 「0は0で割り切れる」とか「0は0の約数である」というと, ちょっと抵抗感を感じるのだが. (p.23)

(考察)

　代数学(方程式の解)に基づいた倍数, 約数として書かれています.

　個人的に一番納得する内容の一つです, 最後の「0は0で割り切れる」とか「0は0の約数である」のくだりも含めて.

 

 

8 : 日本評論社「数とパズルの18話」土井幸雄
数とパズルの18話 (数学ひろば)
posted with カエレバ
土井 幸雄 日本評論社 2006-09
Amazon
楽天市場
 

(倍数・約数の定義)

　整数 { \displaystyle a, b } に対し,

{ \displaystyle a = qb }

なる整数 { \displaystyle q } が存在するとき, { \displaystyle a } は { \displaystyle b } の倍数である, あるいは { \displaystyle b } は { \displaystyle a } の約数であるといい,

{ \displaystyle b|a }

で表す. (p.33)

(その他)

　次の性質は容易に確かめられる(各自チェックせよ):

～中略～

　　(5)　{ \displaystyle a|0  (\forall a\in \mathbb{Z}) } (p.33)

(考察)

　最後の「次の性質」(5)の通り, こちらも「0はaの倍数」であることを認めています.

 

 

9 : 現代数学社「親切な代数学演習 -整数・群・環・体-」加藤明史
親切な代数学演習―整数・群・環・体
posted with カエレバ
加藤 明史 現代数学社 2013-12
Amazon
楽天市場
 

　演習問題付き(簡約されてたりしますが)で初等整数論から群環体まで広く扱った本です.

　ガッツリ学ぶには内容がやや薄いですが項目を振り返るのにとても重宝してます.

(倍数・約数の定義)

　二つの整数 { \displaystyle a\neq 0, b } に対し,

{ \displaystyle b = qa+r,　0\leq r＜|a| }

となるような整数 { \displaystyle q } (商)と { \displaystyle r } (剰余)が一意的に定まる. (p.2)

　前項で, 特に, 剰余 { \displaystyle r = 0 } のとき, { \displaystyle b } は { \displaystyle a } で整除される(割り切れる)といい,

{ \displaystyle a|b } (Landauの記号)

で表す. このとき, { \displaystyle a } は { \displaystyle b } の約数, { \displaystyle b } は { \displaystyle a } の倍数という. (p.2～3)

(その他)

　問題A 2.(抜粋)

　(1)　任意の整数 { \displaystyle a\neq 0 } に対し, { \displaystyle a|a } (反射律). (p.2)

　問題A 3.(抜粋)

　(1)　任意の整数 { \displaystyle a\neq 0 } に対し, { \displaystyle a|0 } (p.2)

(考察)

　その他にある問題からも分かる通り, こちらでもきちんと触れられています.

　また敢えて { \displaystyle a\neq 0 } としているように, 著書では「0は0の約数かどうか」云々の是非を避けています.

 

 

10 : 共立出版株式会社「初等整数論講義 第2版」高木貞治
初等整数論講義 第2版
posted with カエレバ
高木 貞治 共立出版 1971-10-15
Amazon
楽天市場
 

　言わずと知れた高木貞治先生の初等整数論講義です.

　僕は実はまだ平方剰余の前半くらいまでしかマトモに理解してないです…

　キチンと理解して読むには時間的余裕が欲しいですね, 整数論好きにはたまらない, "原著が日本語"という点もオススメです.

(倍数・約数の定義)

　整数の和, 差および積は整数であるが, 商は特別な場合のほかは整数でない. 商 { \displaystyle a/b } が整数 { \displaystyle q } に等しいとき, すなわち

{ \displaystyle a = bq　(b\neq 0) }

のとき, { \displaystyle a } は { \displaystyle b } で割り切れるという. また { \displaystyle a } を { \displaystyle b } の倍数, { \displaystyle b } を { \displaystyle a } の約数という. (p.1)

(その他)

　この定義によれば, { \displaystyle 0 } の任意の整数 { \displaystyle b } (ただし { \displaystyle b\neq 0 } )の倍数である. (p.1)

　{ \displaystyle 0 } は公倍数であるが, それを除けば, 公倍数の中に最も小さい(絶対値において)ものがある. (p.3)

　公約数は絶対値において { \displaystyle a, b, ... } よりも大きいことはありえないから( { \displaystyle a, b, ... } がすべて0である場合を除けば)その中にもっとも大きなものがある. (p.4)

　まず0は0以外のいかなる整数ででも割り切れるから, 無限に多くの約数を有するものといわねばならない. (p.11)

(考察)

　こちらでも前述の「親切な代数学演習」同様, 0の場合を避けています.

　また他の記述で「この定義によれば」とあるように, 「他の定義もありうる」ことを示唆しています.

 

 

細かくみていくとハッキリ決まっていない

　以上10の参考書の記述の通り, 負数はさておき, 0が○○の倍数である…を認めるかどうかははっきりしていません.

　「多数派」として挙げるならば, 整理すれば「そのように定義することもできる」というのが正しい解釈でしょう.

 

 

0を倍数としないことによる「不都合」

　例えば二次方程式の解について考えてみましょう.

　簡単に表現すればあれは実数 { \displaystyle a(\neq 0), b, c }, と対応する実数 { \displaystyle \alpha, \beta } について

{ \displaystyle ax^{2}+bx+c = a(x-\alpha )(x-\beta ) = 0 }

であるとき, 解が { \displaystyle x = \alpha, \beta } である…ということですね.

　今回は都合上, { \displaystyle \alpha \neq \beta } としておきます.

　ここで二つ目に注目しましょう, 例えば { \displaystyle x = \alpha } を代入すれば

{ \displaystyle a(\alpha -\alpha)(\alpha -\beta) = 0 }

{ \displaystyle \leftrightarrow a0(\alpha -\beta) = 0 }

, つまりここに { \displaystyle a0 = 0 } という形が隠れています.

 

　或いは次の簡単な問題を見てみましょう.

(問題)

　{ \displaystyle a } が { \displaystyle b-1 } の2倍となるように, 整数 { \displaystyle a, b(1\leq b\leq 2) } の組を求めよ.

 

　いくら数Aでもこんな簡単な問題はそうそう出てきませんがそういう話は置いといて(途中でそういう状況になったと解釈してください), 右辺は2の倍数ですから, 左辺も2の倍数でなければなりません.

　{ \displaystyle b } は2以下の正の整数ですから { \displaystyle b = 1, 2 } のいずれかです.

　{ \displaystyle b = 2 } の場合は { \displaystyle a = 2 } とすれば良いですが, { \displaystyle b = 1 } の場合は

{ \displaystyle a = 2\times (1-1) = 0 }

　なので { \displaystyle a = 0 } となります, このとき { \displaystyle 0 = 2\times 0 } であり, 「0は2の倍数」であることを自然に受けれ入れていると言えます.

 

　或いは極端なので深く立ち入りませんが, 大学数学で学ぶ「イデアル」という, 見方によっては倍数の拡張概念がありますが, ここにおいて0はとても重要な存在になります.

 

 

0を倍数にすることによる「不都合」

　対して0を倍数にすることで起こりうる問題としては,「0で割り切れる」と誤解して覚えてしまう可能性です.

　0で割ることはタブーを学んだ状況で0を倍数に入れてしまえば, 今まさに学んでいる子が混乱するかもしれませんね.

 

　逆に言えば, 定義次第で十分解決する問題が,止むをえない教育の事情で制限されているために起こりうる誤解とも言えます.

 

　小学校から初等整数論, まして代数学を学ばせるのは無茶というものです, なので「既に体系としてある」のが分かっていても, 例えば今回の倍数の話であればまず自然数から話を進めていき, 学習レベルが上がるにつれ「拡張していく」ことになります.

 

　これは倍数の話に限らないことで, 数学のそういった事情を伏せ, 誤魔化し, 強引に「そういうものだ」としか説明しないごく一部の教師のお陰で, 凝り固まった学生・生徒をいたずらに増やし, 進学して数学となり, 文字を扱い, 空間が拡張され, 概念が抽象化されるにつれ「これまで『そういうものだ』と学んできたこと」がそうでもなかったことに気づき, 混乱し, 結果数学嫌いになってしまうのでは…と, 教育関連に別に関わってもいない立場ですが思うわけです.

　ハッキリ言わずとも, それらしいことをほのめかすだけで, 或いは例外が無いかのような教え方をしないだけで, そういった「数学への誤解」が少しでも解けるんじゃないかと思うわけです.

　数学というのは本当はとても自由で, 良い意味で「都合よく」出来てる世界です.

 

 

自分の状況に合わせた解釈を

　こと教育の場では上で触れた問題があります.

　またこういうった問題を議論する際によく海外の例を挙げる方もいますね.

　いづれもひっくるめて簡単にまとめますが

 

  • 高校数学までの"それ"は, 本来の定義よりも「制限されたもの」と解釈するべき
  • 従って例えば「小学校の教科書ではこうなってる」からといってそれが数学全体の決まりとは限らない
  • 各々の記号や定義は, 時代や地域によってバラバラで, 各々で独自の決まりがなされ, 広まっていった
  • それが現在ある程度「慣例化」したとはいえ, 全世界で全く共通ではない(例えば割り算の記号"÷"は地域によっては"/"です, 分数a/b ( { \displaystyle  \frac{a}{b} } じゃないです, "a/b" です)も地域によっては b/a と書きます)
  • 従って海外のソースは必ずしも日本に当てはまらない

 

　片っ苦しく決めつける必要もありませんし, 自分が知っている範囲が数学のすべてであるというのも必ずしも正しくありません.

 

　数学って, キチッと決まってるようで意外とそうでもないケースが, 細かく掘り下げるとあるものです.

 

thetheorier