もう一人のY君

iPhoneアプリのレビューやアップデートレビューなどを書いています. たまに数学の記事も書きます.

もう一人のY君　MENU

関数～合成関数

数学

 150924_10

　こんにちは, @the_theorierです.

 

 　今回は関数の話です, まぁ以前別サイトで書いたものの焼き直しです.

 

 

関数の定義

 　そもそも関数の定義自体, 時代を経るにつれ変わっていきました.

 

 　基本的には「ある変数に依存して値が決まるような対応や数式など」で構いませんが, 扱う対象がどんどん広がっていき, それに応じて写像(map)や射(arrow)といった拡張概念も生まれています.

 

 　まぁそこまでやるとボリュームがどんどん増えていくので今回は関数に留めます.

 

 　表現は色々あり, 上の通りでも良いですが今回は下のようなものを定義としましょう.

 

 

定義(関数) 

　対象a, b をそれぞれ要素とする集合A, B について, その順序対 { \displaystyle \langle a, b \rangle } を考えます.

　このとき, { \displaystyle f } がAからBへの関数であるとは次の3つを満たすものを言います;

 

{ \displaystyle (1) f }の元はすべて{ \displaystyle \langle a, b \rangle }の形である, ただし { \displaystyle a \in A, b \in B }

{ \displaystyle (2) \langle a, b_{1} \rangle \in f, \langle a, b_{2} \rangle \in f　⇒　b_{1} = b_{2} }

{ \displaystyle (3) A }の任意の元{ \displaystyle a }に対して, { \displaystyle \langle a, b \rangle \in f }となるような{ \displaystyle b \in B }が存在する

 

 　このとき { \displaystyle f : A → B } と書き, 上記を満たす { \displaystyle b \in B } を { \displaystyle f(a) } と書きます.

 

 　写像の場合は明確に区別したりしますが, 関数については { \displaystyle f } が AからBへの関数であるとき, A を定義域(domain)と呼び, { \displaystyle dom(f) } などと書きます.

 

　またBを終域(codomain)と呼び, { \displaystyle cod(f) } などと書きます.

 

 　AからBへの関数 { \displaystyle f } について, { \displaystyle a \in A } が存在するような　{ \displaystyle b \in B }, つまり関数の定義(3)を満たすような { \displaystyle b } をすべて集めた集合を値域(range)と呼び, { \displaystyle ran(f) } などと書きます.

 

 　一般に値域と終域が同じであるとは限りません.

　例えば実数空間の部分集合 { \displaystyle [ 0, \infty ) } から実数空間 { \displaystyle \mathbb{R} } への関数 { \displaystyle y = \sqrt{x} } の場合, 終域は { \displaystyle \mathbb{R} } ですが値域は { \displaystyle [ 0, \infty ) } となります.

 

　これからも分かる通り, 一般に { \displaystyle ran(f) \subseteq cod(f) } という関係が成り立ちます.

 

 　また, A の部分集合 A' の元による { \displaystyle f } の値を集めた集合を, { \displaystyle f } の A' による像(image)と呼び, { \displaystyle Im(f) } と呼びますが, 上記の通りで関数と言ったら始域と定義域は同じであるため, 実質

 

 { \displaystyle Im(f) = ran(f) }

 

 と解釈されます.

　「像」という語は写像で使われることが多いため(必ずしもそうとは言いません), 値域　{ \displaystyle ran(f) } を使う事になるでしょう.

 

　更に突っ込んでおくと, 関数では断りが無い限り, Bに相当する集合を値域自身として議論します, 特に高校数学まででは顕著であり, 従ってこの解釈では

 

{ \displaystyle B = ran(f) = cod(f) }

 

 として良いことになります.

　言葉で言えば「関数とはすなわち, 定義域から値域への対応」ということですね.

 　しかし実際にはそうなるとは限らないわけで(先程の例の通り), これに拘るのは宜しくありません.

 

　以上をまとめると下の図のようになります.

 

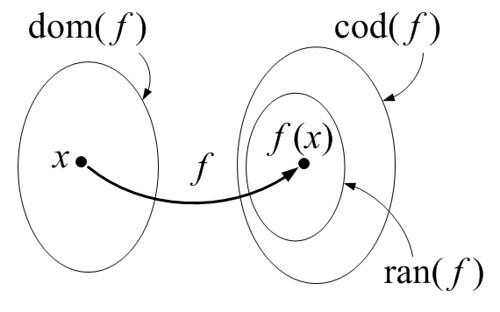
 140425_01

　それぞれの関係が分かるでしょうか？

 

　これ以降は

{ \displaystyle A = dom(f) }

{ \displaystyle B = cod(f) }

{ \displaystyle ran(f) \subset cod(f) }

 として話を進めることにします.

 

 

合成関数

 　2つの関数 { \displaystyle f, g } が存在するとき, それぞれの定義域, 値域の関係によっては { \displaystyle cod(f) } から { \displaystyle dom(g) } へとうまく対応付けることができます.

 

{ \displaystyle ran(f) \supset dom(g) } の場合

 　この場合は下のようになりますね.

 

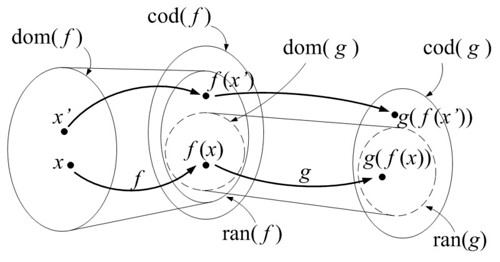
 140425_02

 　この場合, { \displaystyle f } の値域 { \displaystyle ran(f) } の方が  { \displaystyle g } の定義域 { \displaystyle dom(f) } より真に大きいため, { \displaystyle x' } のように { \displaystyle dom(f) } の要素は必ずしも { \displaystyle g } の値域である { \displaystyle ran(g) } の要素になるとは限りません.

 

　つまりこの場合は { \displaystyle f, g } による対応付けは完全ではありませんのでこの2つの関数を使った新しい対応(関数)は作れません.

 

 

{ \displaystyle ran(f) \subseteq dom(g) } の場合

 　この場合は下のようになりますね.

 

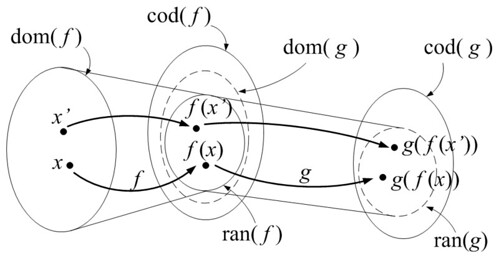
 140425_03

 　この場合, { \displaystyle dom(f) } のすべての要素が { \displaystyle ran(g) } の要素になります.

 

　従って { \displaystyle dom(f) } から { \displaystyle ran(g) } への対応, すなわち関数を定めることができます.

 

 　改めて整理します.

 

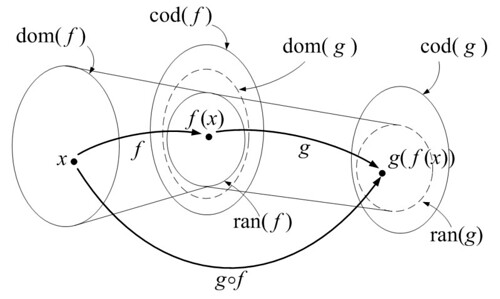
 140425_04

 　二つの関数 { \displaystyle f, g } が { \displaystyle ran(f) \subseteq dom(g) } を満たしているとき, { \displaystyle dom(f) } の任意の要素 { \displaystyle x } は2つの関数 { \displaystyle f, g } により, { \displaystyle ran(g) } の要素へと対応します.

 　このようにして定まる { \displaystyle dom(f) } から { \displaystyle ran(g) } への関数を { \displaystyle f } と { \displaystyle g } の合成関数と呼び, { \displaystyle g \circ f }, 或いは省略して { \displaystyle gf } と書き表します.

 

 

〆

 　取り敢えず図解でイメージしていただけたらと思って書きました, 参考にしてくださいね.

thetheorier