もう一人のY君

iPhoneアプリのレビューやアップデートレビューなどを書いています. たまに数学の記事も書きます.

もう一人のY君　MENU

関数とグラフ, 方程式の解

数学

 

　こんにちは, @the_theorierです.

 

　今回は関数とグラフの関係についてそれなりにちゃんと理解しておこう…という目的で書きます.

 

 

関数が図形を表現するということ

　そもそもなぜ関数がグラフを表すのでしょうか.

　取り敢えず分かりやすく{ \displaystyle n }次元実数空間{ \displaystyle \mathrm{R}^{n} } を使って説明しましょう.

 

 { \displaystyle \mathrm{R}^{n} := \{ (a_{1}, a_{2}, …, a_{n}) | a_{i}\in\mathrm{R}, i = 1, 2, …, n \} }

 

 　ここで { \displaystyle P := (a_{1}, a_{2}, …, a_{n}) }と書くことにし, これを{ \displaystyle (\mathrm{R}^{n} }上の)点と呼びます.

 

 

　次に関数を用意します, 取り敢えず{ \displaystyle n }元変数の実数係数多項式にしましょう, { \displaystyle f(x, y, z) = 2x+y-z^{3} }みたいなものです.

　一般にこういったものを集めた集合を { \displaystyle \mathrm{R}[x_{1}, x_{2}, …, x_{n}] } のように書き表します.

　上と同じように  { \displaystyle X = (x_{1}, x_{2}, …, x_{n}) } と置いて { \displaystyle \mathrm{R}[X] } と書いたりします.

 

 　{ \displaystyle \mathrm{R}[X] } の元から任意に多項式を取ってきて { \displaystyle f = f(x_{1}, x_{2}, …, x_{n}) (= f(X)) } としましょう.

 

 　このとき, 何か具体的な点 { \displaystyle P } を取ってきて, { \displaystyle x_{1} }に{ \displaystyle a_{1} }を, また{ \displaystyle x_{2} }に{ \displaystyle a_{2} }を, …, { \displaystyle x_{n} }に{ \displaystyle a_{n} }を…と置き換えることができますね.

 

　この操作を { \displaystyle f(X) }に点{ \displaystyle P }を代入すると言います.

 

 　今回は{ \displaystyle f(X) }を実数係数多項式としましたから, 点{ \displaystyle P }を代入した結果は必ず実数になります.

　この結果を { \displaystyle f(P) }と表し, ({ \displaystyle f }の, 点{ \displaystyle P }による)値と呼びます.

 

 

グラフを定義する関数

 　点{ \displaystyle P }によっては, 値{ \displaystyle f(P) }が{ \displaystyle 0 }になる場合もあります.

　そこで, { \displaystyle \mathrm{R}[X] }の元{ \displaystyle f(X) }について,

 

 { \displaystyle f(P) = 0 }

 

 を満たす点{ \displaystyle P\in\mathrm{R}^{n} }のことを, ({ \displaystyle f }の)零点と呼びます.

 

 　例えば{ \displaystyle f = x-y }を考えると, { \displaystyle x-y = 0 }となる{ \displaystyle (x, y)\in\mathrm{R}^{2} }は{ \displaystyle (0, 0) }や{ \displaystyle (3, 3) }など色々ありますね.

 

　ではこれをx-y平面にプロットしよう…という話になるわけです.

　条件を満たす点の集合を考えるわけですね, つまり

 

 { \displaystyle V(f) :=\{ P\in\mathrm{R}^{n} | f(P) = 0\} }

 

 という集合ですね.

 

 　もう一度整理すると, この集合 { \displaystyle V(f) } は { \displaystyle \mathrm{R}^{n} } の部分集合であり, 「関数{ \displaystyle f }による { \displaystyle \mathrm{R}^{n} }上の零点をすべて集めた集合」です.

 　このとき{ \displaystyle V(f) }は{ \displaystyle \mathrm{R}^{n} }上において何らかの図形として表され, それを特徴づけるのは関数{ \displaystyle f }に他なりません.

　このとき{ \displaystyle f } を定義関数とし, 集合{ \displaystyle V(f) }を関数集合とでも呼びましょう(正式に「関数集合」という言葉があるかは知りません).

 

 　つまり, この考え方によって関数{ \displaystyle f }が図形を表すことが分かりますね.

 

　この理屈で説明するために陰関数にする事情こそあれ, その辺はなじみのある{ \displaystyle y = f(x) }などの形に直すことは難しくないと思います.

 

 

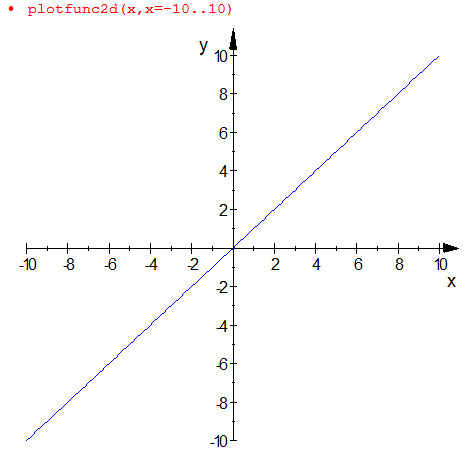
 130419_01

 　例えば { \displaystyle y = x }, つまり { \displaystyle f = x-y }を考えてみます.

　ようはこのグラフは { \displaystyle x-y = 0 } となる { \displaystyle (x, y)\in\mathrm{R}^{2} } を集めた集合に他なりません.

 

　他も同じようにイメージすれば大丈夫です.

 

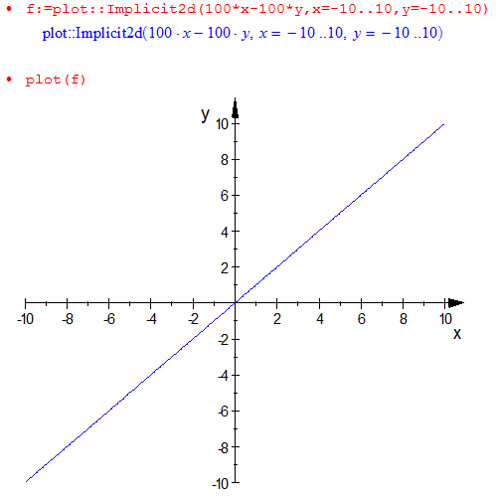
 130419_03

 　しかしこの理屈だと, 例えば上の { \displaystyle f = x-y } に対して例えば { \displaystyle f = 100x-100y } としても, みかけの図形は全く同じです.

 

 　これは { \displaystyle V(f) } を定義した際の零点に関わることで, { \displaystyle V(f) } によって関数を図形で表現するにあたり, { \displaystyle f(P) = 0 } としましたから, { \displaystyle 0 } でない任意の実数 { \displaystyle k } に関して

 

{ \displaystyle f(P) = 0　⇔　k\times f(P) = 0 }

 

 だからです.

 

　従って, 一つの図形を表す定義関数は一通りでなく, 上記のように少なくとも定数倍を無視することで一意的に対応することになります.

 

 

 

グラフと方程式の解

 　{ \displaystyle V(f) } の定義は上記まででは飽くまでも「グラフ」を表現するのに使いました.

　その際関数の零点によって特徴づけたわけですが, それはつまるところ解釈を変えれば零点とはすなわち方程式の解に置きかえられることは直ぐに分かることです.

 

　つまりある方程式 { \displaystyle f(x) = 0 } の解は, その方程式を成す関数 { \displaystyle f } による関数集合 { \displaystyle V(f) } の要素に他なりません.

 

　いやそもそも関数集合などに拘る必要もありませんね, 関数 { \displaystyle f } による零点自体が方程式 { \displaystyle f = 0  } の解ということです.

　つまり関数 { \displaystyle f } の解集合とは上記の { \displaystyle V(f) } そのものということです.

 

　零点とか解とか言って表現が異なるのは, それをどのようなカテゴリで解釈しているか…の違いであり, 見ている部分は実際は同じであったりします.

 

 　例えばより拡張して準同型の世界における核(Kernel)は, 例えば同種の構造を持つ二つの集合{ \displaystyle A, B }における準同型写像 { \displaystyle f : A → B } について

 

 { \displaystyle ker(f) := \{ (a_{1}, a_{2})\in A\times A | f(a_{1}) = f(a_{2})\} }

 

 とします(同種である構造の種類によって表現が違ったりします).

　少し変形すれば { \displaystyle V(f) } のそれと似ていますね.

 

 　或いはもっとなじみあるベクトル空間で言うと, 線形写像 { \displaystyle F : U → V } における集合 { \displaystyle ker(F) \subset U } を意味します.

 

 { \displaystyle ker(F) := \{\boldsymbol{u}\in U | F(\boldsymbol{u}) = 0\} }

 

 

thetheorier