もう一人のY君

iPhoneアプリのレビューやアップデートレビューなどを書いています. たまに数学の記事も書きます.

もう一人のY君　MENU

二項定理を用いた平方根、立方根の近似

数学

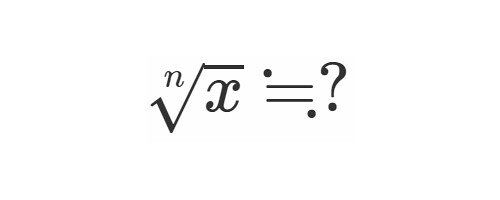
160729_00

　今日は二項定理を使ったn乗根近似のお話です.

 

スポンサーリンク

 
[Contents]
 

 

 

二項定理とは

　通常, 二項定理とは二項係数 { \displaystyle \binom{n}{m} } { \displaystyle \bigl( m \geq n \geq 0,\quad m, n\in\mathbb{Z} \bigr) } における

 

{ \displaystyle (x+y)^{n} = }{ \displaystyle \binom{n}{0}x^{0}y^{n}+\binom{n}{1}x^{1}y^{n-1}+ } … { \displaystyle +\binom{n}{n}x^{n}y^{0} }

 

であることはよく知られています.

 

　これは応用すれば整数でなくとも有理数や複素数にまで拡張が可能です.

　特に上で { \displaystyle x } を { \displaystyle 1 } に, { \displaystyle y } を { \displaystyle x } に置き変え, 更に { \displaystyle x } は { \displaystyle |x|\lt 1 } を満たす複素数とすれば

 

{ \displaystyle (1+x)^{n} = }{ \displaystyle \sum_{k=0}^{k}\binom{n}{k}x^{k} }

 

とできます.

　{ \displaystyle |x|\lt 1 } ですから, { \displaystyle x^{k} } は { \displaystyle k } が大きくなるにつれ十分無視できます, つまり近似式として使えるわけです.

 

　複素数を扱うため, 通常の二項係数でなく言うなれば「一般二項係数」として評価します.

 

[定義：一般二項係数]

　複素数 { \displaystyle \alpha } と非負整数 { \displaystyle k } に対して,

{ \displaystyle \binom{\alpha}{k} = \begin{cases} \frac{\alpha(\alpha-1)...(\alpha-k+1)}{k!} \quad (k\geq 1) \\ 1 \quad (k=0) \end{cases} }

 

　断りが無ければここではこれを二項係数と呼ぶことにします.

　従って上の等式も次のように書き換えられます.

 

{ \displaystyle (1+x)^{\alpha} = \sum_{k=0}^{k}\binom{\alpha}{k}x^{k}\quad |x|\lt 1 }

 

　更に言うと, 一般二項係数を利用すれば上記で { \displaystyle \sum } を { \displaystyle k } までで止め置く必要もありません, つまり

 

{ \displaystyle (1+x)^{\alpha} = \sum_{k=0}^{\infty}\binom{\alpha}{k}x^{k}\quad |x|\lt 1 }

 

としてしまっても問題ありません.

 

　また複素数で扱う場合は実際には二項係数でなく「ポッホハンマー記号」と名を変えますが, その意味する所は似ています.

[定義：ポッホハンマー記号]

　複素数 { \displaystyle \alpha } と非負整数 { \displaystyle k } について,

{ \displaystyle \bigl(\alpha\bigr)^{k} := \begin{cases} \alpha(\alpha+1)...(\alpha+k-1) \quad (k\geq 1) \\ 1 \quad (k=0) \end{cases} }

 

{ \displaystyle \bigl(\alpha\bigr)_{k} := \begin{cases} \alpha(\alpha-1)...(\alpha-k+1) \quad (k\geq 1) \\ 1 \quad (k=0) \end{cases} }

　2つありますがどちらも同じ呼び名のようです, また記号も参考書によっては違う可能性があります.

 

 

一般二項定理による近似公式

　上記の一般二項定理とポッホハンマー記号をうまく組み合わせることで, 次の等式を得ます.

 

[近似公式]

{ \displaystyle (1\pm x)^{-\alpha} = \sum_{k=0}^{\infty}\frac{\bigl(\alpha\bigr)^{k}}{k!}\bigl(\mp x\bigr)^{k} , |x|\lt 1 }

 

　例えば { \displaystyle \alpha = 1 } とすれば

 

{ \displaystyle \frac{1}{1+x} = 1-x+x^{2}-x^{3}+… }
{ \displaystyle \frac{1}{1-x} = 1+x+x^{2}+x^{3}+… }

 

という有名な近似式が, また { \displaystyle \alpha = \frac{1}{2}, -\frac{1}{3}, \frac{1}{3} } とすれば

 

 { \displaystyle \frac{1}{\sqrt{1\pm x}}= } { \displaystyle 1\mp \frac{1}{2}x+\frac{1\cdot 3}{2\cdot 4}x^{2} } { \displaystyle \mp \frac{1\cdot 3\cdot 5}{2\cdot 4\cdot 6}x^{3}+\ldots }

 

 { \displaystyle \sqrt[3]{1\pm x} = } { \displaystyle 1\pm \frac{1}{3}x - \frac{1\cdot 2}{3\cdot 6}x^{2} } { \displaystyle \pm\frac{1\cdot 2\cdot 5}{3\cdot 6\cdot 9}x^{3}-\ldots }

 

{ \displaystyle \frac{1}{\sqrt[3]{1\pm x}} = } { \displaystyle 1\pm \frac{1}{3}x + \frac{2}{3^{2}}x^{2} } { \displaystyle \pm \frac{2\cdot 7}{3^{4}}x^{3}+\ldots }

 

…と言う風に求めることができます.

 

　これらを上手いこと使って具体的な近似式を作っていくわけです.

 

 

√2の場合

　まずは { \displaystyle \sqrt{2} } で試してみましょう.

　工夫を要するんですが以下のようになります.

 

{ \displaystyle \bigl( 1-\frac{2}{100} \bigr)^{-\frac{1}{2}} }

{ \displaystyle = \Bigl( \frac{98}{100} \Bigr)^{-\frac{1}{2}} = \Bigl( \frac{100}{98} \Bigr)^{\frac{1}{2}} }

{ \displaystyle = \Bigl( \frac{10^{2}}{7^{2}\cdot 2} \Bigr)^{\frac{1}{2}} }

{ \displaystyle = \frac{10}{7}\cdot \frac{1}{\sqrt{2}} }

{ \displaystyle = \frac{10}{7}\cdot \frac{\sqrt{2}}{2} }

{ \displaystyle = \frac{10}{14}\sqrt{2} }

 

となるので,

 

{ \displaystyle \sqrt{2} }

{ \displaystyle = \frac{14}{10}\Bigl( 1-\Bigl( \frac{2}{100} \Bigr) \Bigr)^{-\frac{1}{2}} }

{ \displaystyle = \frac{14}{10}  \{1+\Bigl(\frac{1}{2}\cdot\frac{2}{100}  + \frac{1\cdot 3}{2\cdot 4}\cdot\Bigl( \frac{2}{100} \Bigr)^{2}   } { \displaystyle + \frac{1\cdot 3\cdot 5}{2\cdot 4\cdot 6 }\cdot \Bigl( \frac{2}{100} \Bigr)^{3}+\dots\} }

{ \displaystyle = \frac{14}{10} \{ 1+\frac{1}{100} + \frac{3}{2}\cdot\Bigl(\frac{1}{100}\Bigr)^{2} } { \displaystyle + \frac{5}{2}\cdot \Bigl(\frac{1}{100}\Bigr)^{3}+\dots\} }

{ \displaystyle = 14\cdot \frac{1}{10} + 14\cdot\Bigl(\frac{1}{10}\Bigr)^{3} } { \displaystyle + 21\cdot\Bigl( \frac{1}{10} \Bigr)^{5} + 35\cdot \Bigl( \frac{1}{10} \Bigr)^{7}\dots }

{ \displaystyle = 1.4+0.014+0.00021+0.0000035+\dots }

{ \displaystyle = 1.4142135\dots }

 

となります.

 

　実際 { \displaystyle \sqrt{2} = 1.414214562371\dots } ですから正しい十分近い数であることが分かります.

 

 

その他

　他の例を見てみましょう(分かる範囲でのみやってます).

 

√3のとき

{ \displaystyle \Bigl( 1+\frac{8}{100} \Bigr)^{-\frac{1}{2}} = \frac{10}{18}\sqrt{3} } より,

{ \displaystyle \sqrt{3} }

{ \displaystyle = \frac{18}{10}\Bigl( 1+\frac{8}{100} \Bigr)^{-\frac{1}{2}} }

{ \displaystyle = \frac{18}{10} \{ 1-\frac{1}{2}\frac{8}{100}+ } { \displaystyle  \frac{1\cdot 3}{2\cdot 4}\Bigl( \frac{8}{100} \Bigr)^{2} - \frac{1\cdot 3\cdot 5}{2\cdot 4\cdot 6}\Bigl( \frac{8}{100} \Bigr)^{3}\dots\} }

{ \displaystyle = \frac{18}{10}\{ 1-4 \Bigl( \frac{1}{10} \Bigr)^{2} + } { \displaystyle 24 \Bigl( \frac{1}{10} \Bigr)^{4} - 160 \Bigl( \frac{1}{10} \Bigr)^{6}\dots\} }

{ \displaystyle = \frac{18}{10} - 72 \Bigl( \frac{1}{10} \Bigr)^{3} + 432 \Bigl( \frac{1}{10} \Bigr)^{5} } { \displaystyle - 2880 \Bigl( \frac{1}{10} \Bigr)^{7}+\dots }

{ \displaystyle = 1.8 - 0.072 + 0.00432 } { \displaystyle - 0.000288+\dots }

{ \displaystyle = 1.732032\dots }

 

[実際の値]

{ \displaystyle \sqrt{3} = 1.732050\dots }

 

 

√5のとき

{ \displaystyle \Bigl( 1-\frac{20}{100} \Bigr)^{-\frac{1}{2}} = \frac{1}{2}\sqrt{5} } より,

{ \displaystyle \sqrt{5} }

{ \displaystyle = 2\Bigl( 1-\frac{20}{100} \Bigr)^{-\frac{1}{2}} }

{ \displaystyle = 2 \{ 1+\frac{1}{2}\frac{20}{100}+ } { \displaystyle  \frac{1\cdot 3}{2\cdot 4}\Bigl( \frac{20}{100} \Bigr)^{2} + \frac{1\cdot 3\cdot 5}{2\cdot 4\cdot 6}\Bigl( \frac{20}{100} \Bigr)^{3}\dots\} }

{ \displaystyle = 2\{ 1+10 \Bigl( \frac{1}{10} \Bigr)^{2} + } { \displaystyle 150 \Bigl( \frac{1}{10} \Bigr)^{4} + 2500 \Bigl( \frac{1}{10} \Bigr)^{6}\dots\} }

{ \displaystyle = 2 + 0.2 + 0.03 +0.005+\dots }

{ \displaystyle = 2.235\dots }

 

[実際の値]

{ \displaystyle \sqrt{3} = 2.236067\dots }

 

 

√6のとき

{ \displaystyle \Bigl( 1-\frac{4}{100} \Bigr)^{-\frac{1}{2}} = \frac{10}{24}\sqrt{6} } より,

{ \displaystyle \sqrt{6} }

{ \displaystyle = \frac{24}{10}\Bigl( 1-\frac{4}{100} \Bigr)^{-\frac{1}{2}} }

{ \displaystyle = \frac{24}{10} \{ 1+\frac{1}{2}\frac{4}{100}+ } { \displaystyle  \frac{1\cdot 3}{2\cdot 4}\Bigl( \frac{4}{100} \Bigr)^{2} + \frac{1\cdot 3\cdot 5}{2\cdot 4\cdot 6}\Bigl( \frac{4}{100} \Bigr)^{3}\dots\} }

{ \displaystyle = \frac{24}{10}\{ 1+2 \Bigl( \frac{1}{10} \Bigr)^{2} + } { \displaystyle 6 \Bigl( \frac{1}{10} \Bigr)^{4} + 20 \Bigl( \frac{1}{10} \Bigr)^{6}\dots\} }

{ \displaystyle = 2.4 + 0.048 + 0.00144 +0.000048+\dots }

{ \displaystyle = 2.449488\dots }

 

[実際の値]

{ \displaystyle \sqrt{3} = 2.449489\dots }

 

 

√7のとき

{ \displaystyle \Bigl( 1+\frac{12}{100} \Bigr)^{-\frac{1}{2}} = \frac{10}{28}\sqrt{7} } より,

{ \displaystyle \sqrt{7} }

{ \displaystyle = \frac{28}{10}\Bigl( 1+\frac{12}{100} \Bigr)^{-\frac{1}{2}} }

{ \displaystyle = \frac{28}{10} \{ 1-\frac{1}{2}\frac{12}{100}+ } { \displaystyle  \frac{1\cdot 3}{2\cdot 4}\Bigl( \frac{12}{100} \Bigr)^{2} - \frac{1\cdot 3\cdot 5}{2\cdot 4\cdot 6}\Bigl( \frac{12}{100} \Bigr)^{3}\dots\} }

{ \displaystyle = \frac{28}{10}\{ 1-6 \Bigl( \frac{1}{10} \Bigr)^{2} + } { \displaystyle 54 \Bigl( \frac{1}{10} \Bigr)^{4} - 540 \Bigl( \frac{1}{10} \Bigr)^{6}\dots\} }

{ \displaystyle = 2.8 - 0.168 + 0.01512 - 0.001512+\dots }

{ \displaystyle = 2.645608\dots }

 

[実際の値]

{ \displaystyle \sqrt{3} = 2.645751\dots }

 

 

√8のとき

{ \displaystyle \Bigl( 1+\frac{28}{100} \Bigr)^{-\frac{1}{2}} = \frac{10}{32}\sqrt{8} } より,

{ \displaystyle \sqrt{8} }

{ \displaystyle = \frac{32}{10}\Bigl( 1+\frac{28}{100} \Bigr)^{-\frac{1}{2}} }

{ \displaystyle = \frac{32}{10} \{ 1-\frac{1}{2}\frac{28}{100}+ } { \displaystyle  \frac{1\cdot 3}{2\cdot 4}\Bigl( \frac{28}{100} \Bigr)^{2} - \frac{1\cdot 3\cdot 5}{2\cdot 4\cdot 6}\Bigl( \frac{28}{100} \Bigr)^{3}\dots\} }

{ \displaystyle = \frac{32}{10}\{ 1-14 \Bigl( \frac{1}{10} \Bigr)^{2} + } { \displaystyle \frac{21}{2} \Bigl( \frac{1}{10} \Bigr)^{4} - 6860 \Bigl( \frac{1}{10} \Bigr)^{6}\dots\} }

{ \displaystyle = 3.2 - 0.448 + 0.00336 - 0.021952+\dots }

{ \displaystyle = 2.733408\dots }

 

[実際の値]

{ \displaystyle \sqrt{3} = 2.828427\dots }

 

 

√10のとき

{ \displaystyle \Bigl( 1-\frac{10}{100} \Bigr)^{-\frac{1}{2}} = \frac{10}{30}\sqrt{10} } より,

{ \displaystyle \sqrt{10} }

{ \displaystyle = \frac{30}{10} \Bigl( 1-\frac{10}{100} \Bigr)^{-\frac{1}{2}} }

{ \displaystyle = \frac{30}{10} \{ 1+\frac{1}{2}\frac{10}{100}+ } { \displaystyle  \frac{1\cdot 3}{2\cdot 4}\Bigl( \frac{10}{100} \Bigr)^{2} + \frac{1\cdot 3\cdot 5}{2\cdot 4\cdot 6}\Bigl( \frac{10}{100} \Bigr)^{3}\dots\} }

{ \displaystyle = \frac{30}{10} \{ 1+5 \Bigl( \frac{1}{10} \Bigr)^{2} + } { \displaystyle \frac{75}{2} \Bigl( \frac{1}{10} \Bigr)^{4} + \frac{625}{2} \Bigl( \frac{1}{10} \Bigr)^{6}\dots\} }

{ \displaystyle = 3 + 0.15 + 0.01125 +0.0009375+\dots }

{ \displaystyle = 3.1621875\dots }

 

[実際の値]

{ \displaystyle \sqrt{3} = 3.1622766\dots }

 

　近いものもあればかなり精度の低いものまで様々です.

　なお, { \displaystyle \Bigl( 1\pm \frac{a}{100} \Bigr)^{-\frac{1}{2}} } { \displaystyle = \frac{10}{b}\sqrt{p} } となる { \displaystyle a, b, p } を見つけるためには, { \displaystyle \frac{a}{100} } の部分が

 

{ \displaystyle \frac{2m}{10^{2n}} }

 

という形になるよう選ぶと良さそうです.

　また計算の手間上, { \displaystyle 2m } の部分はできるだけ小さい方が良いです.

　実際にはそう都合よく行きませんが.

 

　上手いこと式を見つけても, 結果的に手間がかかる場合もあります.

 

 　試しに立方根についてもやってみましょう, こちらはもっと精度が悪く, 手間もかかります.

　平方根とはまたテクニックも違ってきます.

 

 

2の立方根のとき

{ \displaystyle \sqrt[3]{2} }

{ \displaystyle = \sqrt[3]{\frac{2^{10}}{2^{9}}} = \frac{1}{8}\sqrt[3]{1000+24} }

{ \displaystyle = \frac{10}{8}\Bigl( 1+\frac{24}{1000} \Bigr)^{\frac{1}{3}} }

 より,

{ \displaystyle \sqrt[3]{2} }

{ \displaystyle = \frac{10}{8}\Bigl( 1+\frac{24}{1000} \Bigr)^{\frac{1}{3}} }

{ \displaystyle = \frac{10}{8} \{ 1+\frac{1}{3}\frac{24}{100} } { \displaystyle  -\frac{1\cdot 2}{3\cdot 6}\Bigl( \frac{24}{1000} \Bigr)^{2} + \frac{1\cdot 2\cdot 5}{3\cdot 6\cdot 9}\Bigl( \frac{24}{1000} \Bigr)^{3}\dots\} }

{ \displaystyle = \frac{10}{8}\{ 1+8 \Bigl( \frac{1}{10} \Bigr)^{3} } { \displaystyle - 64 \Bigl( \frac{1}{10} \Bigr)^{6} + \frac{2560}{3} \Bigl( \frac{1}{10} \Bigr)^{9}\dots\} }

{ \displaystyle = 1.25 + 0.01 - 0.000008 -  } { \displaystyle 0.0010666666 - \dots }

{ \displaystyle = 1.26105866\dots }

 

[実際の値]

{ \displaystyle \sqrt{3} = 1.25992104\dots }

 

 

4の立方根のとき

{ \displaystyle \sqrt[3]{4} }

{ \displaystyle = \sqrt[3]{\frac{4^{7}}{4^{6}}} = \frac{1}{16}\sqrt[3]{1000+24} }

{ \displaystyle = \frac{10}{16}\Bigl( 1+\frac{24}{1000} \Bigr)^{\frac{1}{3}} }

 より,

{ \displaystyle \sqrt[3]{4} }

{ \displaystyle = \frac{16}{10}\Bigl( 1+\frac{24}{1000} \Bigr)^{\frac{1}{3}} }

{ \displaystyle = \frac{16}{10} \{ 1-\frac{1}{3}\frac{24}{100} } { \displaystyle  +\frac{4}{3^{2}}\Bigl( \frac{24}{1000} \Bigr)^{2} - \frac{2\cdot 7}{3^{4}}\Bigl( \frac{24}{1000} \Bigr)^{3}\dots\} }

{ \displaystyle = \frac{16}{10}\{ 1-8 \Bigl( \frac{1}{10} \Bigr)^{3} } { \displaystyle + 256 \Bigl( \frac{1}{10} \Bigr)^{6} - \frac{7168}{3} \Bigl( \frac{1}{10} \Bigr)^{9}\dots\} }

{ \displaystyle = 1.26 - 0.0128 - 0.0004096 -  } { \displaystyle 0.000003822933 - \dots }

{ \displaystyle = 1.58760577706666\dots }

 

[実際の値]

{ \displaystyle \sqrt{3} = 1.58740105196819\dots }

 

 

5の立方根のとき

{ \displaystyle \sqrt[3]{5} }

{ \displaystyle = \sqrt[3]{\frac{5^{4}}{5^{3}}} = \frac{1}{5}\sqrt[3]{1000-375} }

{ \displaystyle = \frac{10}{5}\Bigl( 1-\frac{375}{1000} \Bigr)^{\frac{1}{3}} }

 より,

{ \displaystyle \sqrt[3]{5} }

{ \displaystyle = \frac{10}{5}\Bigl( 1+\frac{375}{1000} \Bigr)^{\frac{1}{3}} }

{ \displaystyle = 2 \{ 1-\frac{1}{3}\frac{375}{1000} } { \displaystyle  -\frac{2}{3\cdot 9}\Bigl( \frac{375}{1000} \Bigr)^{2} - \frac{1\cdot 2\cdot 5}{3\cdot 6\cdot 9}\Bigl( \frac{375}{1000} \Bigr)^{3}-\dots\} }

{ \displaystyle = 2\{ 1-125 \Bigl( \frac{1}{10} \Bigr)^{3} } { \displaystyle - 15625 \Bigl( \frac{1}{10} \Bigr)^{6} - \frac{9765625}{3} \Bigl( \frac{1}{9} \Bigr)^{9}\dots\} }

{ \displaystyle = 2 - 0.25 - 0.03125 -  } { \displaystyle 0.00651041666 - \dots }

{ \displaystyle = 1.712239583333\dots }

 

[実際の値]

{ \displaystyle \sqrt{3} = 1.709975946676\dots }

 

　これ以上は考えるのはしんどいので限界でした^^;

　暇な方は試してみてください.

 

 

 [参考] 日本評論社「数学セミナー 2013年3月号 特集『二項定理を深く学ぼう』」

 

 

 

thetheorier