もう一人のY君

iPhoneアプリのレビューやアップデートレビューなどを書いています. たまに数学の記事も書きます.

もう一人のY君　MENU 　MENU

サイコロの目が出る確率はなぜ1/6なのか

数学

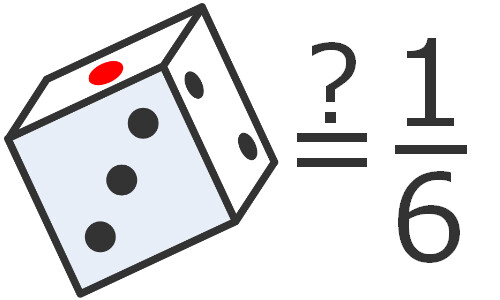
 151212_05

 　よく聞かれる問題です.

 

出るか出ないかの2通りだから{ \displaystyle \frac{1}{2} }?

 　たまにこういうのを聞きます, そんなわけないんですが.

　でも理解してもらうには根拠を示さなければ.

 

 

確率空間

 　まず最低限のことを書いておきましょう.

　とは言ってもガチの確率空間を語ると長くなるし余り意味が無いので割愛します.

 　標本空間 { \displaystyle \Omega = \{ 1, 2, 3, 4, 5, 6 \} } を用意します.

　{ \displaystyle \Omega } は有限集合なので { \displaystyle \Omega } 上の加法族 { \displaystyle \Sigma_0 } は同時に { \displaystyle \Omega } 上の { \displaystyle \sigma }-加法族です.

 

 　よって { \displaystyle (\Omega, \Sigma_0) } は測度空間であり, この上に測度 { \displaystyle \mu_0 } を与えることができます.

　この { \displaystyle \mu_0 } を { \displaystyle \mu_0(\Omega) = 1 } を満たすように定めれば, 三つ組 { \displaystyle (\Omega, \Sigma_0, \mu_0) } は晴れて確率空間となります.

 

　扱いを楽にするために, 今後は { \displaystyle P = \mu_0 } とします.

 

条件

 　問題はどのように { \displaystyle P } を定めるか…ですが, 少なくとも定義から

 

  • { \displaystyle P : \Sigma_0 \to [0, \infty) } によって定義される非負集合関数
  • { \displaystyle P(\bigcup_{i\leq n} F_i) \leq \sum_{i\leq n} P(F_i),　(F_i \in\Sigma_0, i = 0, 1, 2,..., n) }

 

 は必要です.

　前者は { \displaystyle P } が測度であるための定義であり, また後者は測度空間ならば成り立つ定理です.

 　また"これから決める"ので実際に { \displaystyle P(F_i) } が何なのかはこの時点では分かりません.

　なお何となく分かるでしょうが { \displaystyle F_i } は, 今回は「i の目が出る事象」 ですね.

　{ \displaystyle n = 6 } であることも分かると思います.

 

観察して分かる事実

 　まず, 今回は1回しか投げませんから, 出目が被ることはどう考えてもあり得ません.

　つまり

 { \displaystyle F_i\cap F_j = \emptyset,　(i, j \in \{1, 2, 3, 4, 5, 6\},　i \neq j) }

 , つまり事象は互いに独立です.

 

 　{ \displaystyle P } の加法性と上記の独立性から

 { \displaystyle P(\bigcup_{i\leq 6} F_i) = \sum_{i\leq 6} P(F_i),　(F_i\in\Sigma_0,　i = 1, 2, 3, 4, 5, 6) }

 であり, { \displaystyle \bigcup_{i\leq 6} F_i } は標本空間 { \displaystyle \Omega } そのものですから, 結局

 { \displaystyle \sum_{i\leq 6} P(F_i) = 1 }　…(1)

 が分かります.

 

仮定を採用する

 　「出るか出ないかの2通りだから{ \displaystyle \frac{1}{2} }である」を認めましょう.

　つまりどの目が出ようとも各々の確率は { \displaystyle \frac{1}{2} } です, これを(1)に代入すると

 { \displaystyle \sum_{i=1, 2, ..., 6} \frac{1}{2} = 1 }

⇔　{ \displaystyle \frac{1}{2}\times 6 = 1 }

⇔　{ \displaystyle 3 = 1 }

 , これは明らかに矛盾しています.

 　つまりこれは仮定が間違っている…ということです/

 

「出るか出ないか」の曲解

 　実際その目が出るか出ないか…は正しいです.

　ではなぜ { \displaystyle \frac{1}{2} }  ではないのか.

 

 　それは至極簡単な話で, この「出るか出ないか」というのは飽くまでも { \displaystyle 0＜p＜1 } を満たす実数 { \displaystyle p } について

  • 出る　→　{ \displaystyle p }
  • 出ない　→　{ \displaystyle 1-p }

 であるに過ぎないからです.

　そして { \displaystyle \frac{1}{2} } になると主張する方は, 根拠なく { \displaystyle p = \frac{1}{2} } であると決めつけているだけというわけです.

 　現実に言えるのはただ { \displaystyle 0＜p＜1 } である…というだけで, この時点ではだれも { \displaystyle p=\frac{1}{2} } だなんて言ってないのです.

 

 　そして理想的な確率空間では { \displaystyle p=\frac{1}{6} } である…というわけですね.

 

 

 

 

thetheorier