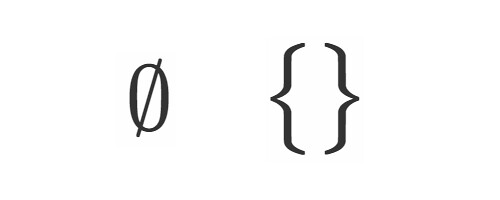
学んだばかりの時は特にイメージがつかみにくいですよね.
「中身が空っぽの袋」でも良いんですがもうちょっと数学らしく説明することにします.
スポンサーリンク
空集合の定義
初っ端から書いておきましょう.
空集合とは, 任意の要素を持たない集合のことを言います, ちゃんと書くと
を満たす集合 を指し,
や
などと書きあらわします.
部分集合の定義
次は部分集合です.
2つの集合 が存在し,
何を示せば良いか
空集合, そして部分集合の定義から, 目的を達成するには
(Thm 1)
任意の集合 について
.
, これが成り立てば良いことが分かります.
(ちょっと脱線)推論図について
今回の証明では推論図というものを使います, 大学数学科でやっと触れるかどうかの「道具」なんですが慣れれば難しくありません.
数学, 特に論理学では, 演繹論理というものを扱います, つまり一般的な法則にしたがって, いくつかの仮定や前提から個々の結論を導きます1.
逆に個々の結論を用いて, 一定の法則を導くことを帰納論理と言います, 例えば科学がこれに当てはまります.
勿論数学や科学それぞれが完全にこの一方だけ…というわけではありません.
更に脱線するならば学校教育における「算数」は帰納論理, 「数学」は演繹論理に偏っていると考えることもできます.
実際の数学はどちらも重要になってきます.
推論図はこの演繹論理の流れを表す方法の一つになります.
例えばAという命題からBという命題が演繹によって導かれたとします, これは
という2つの前提からBという結論を導いたと解釈できます.
この「推論規則」と呼ばれる流れを, 推論図では以下のように書き表します.
この図式を推論図と言います.
もうちょっと複雑にしてみると,
これは左上で と
という前提から
という結論を, また右上で
と
という前提から
という結論を導き, 各々の結論を更に前提として
という結論を導いているわけです.
言いかえれば
の3つの前提から という結論を導いています.
さて, 上の事実は
のみを前提とすれば, これは「 という仮定から
という結論を導いた」とも言えます.
このように解釈した場合, 推論図では下のように書き表します.
| 1 | |
(どうも推論規則のLaTeXが分からないので綺麗じゃないですがご容赦を.)
ここで上に2つあるAの上に書いてある1は, Aという仮定が最後の推論
を行ったときに削除されたことを意味します, これによって
の2つの前提から結論 を導いたことになります.
推論規則は他にもたくさんありますが今回はここまでとします.
矛盾の性質
いま, 矛盾という命題と とすることにし, 更に
が正しいことを認めましょう(これが正しいことを証明するには, 矛盾の存在を認めねばなりません).
すると以下によって を導くことができます.
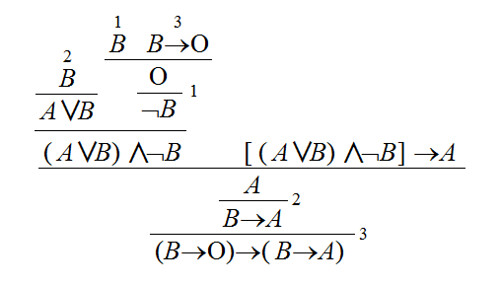
ここで とすれば
となりますね.
任意の命題 A について
| 1 |
であることが分かりますから, は正しいことが分かります.
正しい前提は削除しても問題ありませんから(正しいものを仮定してもしなくても"それ以降"は同じですね?), 結果これは
ということになります.
これはつまり
矛盾からは任意の命題が導かれる
ことを意味しています, そしてこれが矛盾という命題そのものの性質となります.
Thm 1の証明
では目的の証明をしましょう.
空集合の定義から, 任意のの元 について
は矛盾命題 です.
先程の矛盾命題の性質から, からは任意の命題が導かれます, つまり任意の集合
について
は真です.
よって部分集合の定義から
が言えます. //
〆
言ってしまえば, 空集合が任意の集合の部分集合であることは定義そのものとして良いわけです.
因みに とすれば
であることも分かります.
