もう一人のY君

iPhoneアプリのレビューやアップデートレビューなどを書いています. たまに数学の記事も書きます.

もう一人のY君　MENU 　MENU

スツルムの定理

数学

 150926_02

　こんにちは, @the_theorierです.

 

　今回は高校数学まででは学びませんが知っておくと便利なスツルムの定理を紹介します.

 

 

スツルムの定理で分かること

　簡単に言えば, 実数係数多項式による方程式について, 指定した区間における実数解の個数を与える定理です.

 

　現実的ではありませんが理屈では実数解近似にも使えますね.

 

　定理を紹介するためにいくつか準備をします.

 

　まず{ \displaystyle n }次の実数係数多項式として次を定めます.

 

{ \displaystyle f(x) = a_{n}x^{n} + a_{n-1}x^{n-1} + … + a_{1}x + a_{0} }

{ \displaystyle (a_{i}\in\mathrm{R},　i = 0, 1, 2, …, n,　a_{n}\neq 0) }

 

 　{ \displaystyle f(x) } は明らかに任意の { \displaystyle x\in\mathrm{R} } で微分可能ですから, { \displaystyle x } で一回微分できます.

 

 　次に { \displaystyle f(x) } 自身とこれを { \displaystyle x } で微分した { \displaystyle f'(x) } を使い, ユークリッドの互除法の要領で商と余りを求めていきます, つまり

 

 { \displaystyle f(x) = f'(x)Q_{0}(x) + r_{0}(x) }

{ \displaystyle f'(x) = r_{0}(x)Q_{1}(x) + r_{1}(x) }

{ \displaystyle r_{0} = r_{1}(x)Q_{2}(x) + r_{2}(x) }

…

{ \displaystyle r_{m-2}(x) = r_{m-1}(x)Q_{m}(x) + r_{m}(x) }

{ \displaystyle r_{m-1}(x) = r_{m}(x)Q_{m+1}(x) }　　…(※)

 

…という感じです.

　但し{ \displaystyle Q_{i}, r_{i} } は多項式で { \displaystyle deg(r_{0}) }＜{ \displaystyle def(f) }, { \displaystyle deg(r_{i+1}) }＜{ \displaystyle deg(r_{i}), i=0, 1, 2, …, m } であるとします.

 

 　このようにしていくと, 最後に得られた { \displaystyle r_{m}(x) } は, 言ってみれば { \displaystyle f(x) } と { \displaystyle f'(x) } の最大共通因子となります, 互いに数であれば「最大公約数」ですね.

 　この関数列 { \displaystyle r_{m}(x) } を用いて, 以下の関数列 { \displaystyle \{ f_{n}(x)\} } を新たに定めます.

 

 { \displaystyle f(_{0}) := f(x) }

{ \displaystyle f_{1}(x) := f'(x) }

\begin{equation} f_{k}(x)= \left \{\begin{array}{l}-r_{k-2}(x),　k=2, 3, 6, 7,… \\r_{k-2}(x),　k=4, 5, 8, 9,…\end{array}\right.\end{equation}

 

 　{ \displaystyle m = 2 } 以降は2つおきにマイナスを付けます.

　この関数列 { \displaystyle \{ f_{m}(x)\} } をスツルム列と呼びます.

 

 　次に, 任意の実数点 { \displaystyle x = a } を各スツルム列に代入し, 得た値の列から符号の入れ替わった回数を数えます.

　但し途中で0になった個所は, それを飛ばして数えます.

 

　例えば代入して得た値の列が

 

{ \displaystyle 1, \dfrac{2}{3}, -12, 0, \dfrac{1}{5} }

 

 だった場合, これを符号で解釈すれば

 

{ \displaystyle +　+　-　0　+ }

 

 ですから, 符号の入れ替わった回数は2となりますね.

 

 　このようにして得た数を { \displaystyle V(a) } と書き表します.

 

 　これを用いてスツルムの定理となります.

 

 

スツルムの定理

　実数係数多項式 { \displaystyle f(x) } は, 実数による方程式 { \displaystyle f(x) = 0 } が, 重解を持たず, かつ実数 { \displaystyle a, b } に対して { \displaystyle f(a)\neq 0, f(b)\neq 0 } であるとする.

　このとき開区間 { \displaystyle (a, b) } における方程式 { \displaystyle f(x) = 0 } の実数解の個数 { \displaystyle N } について

 

{ \displaystyle N = V(a) - V(b) }

 

 

例

 　例えば区間{ \displaystyle (0, 2) } における, 方程式 { \displaystyle f(x) = x^{3}-5x+4 = 0 } の実数解の個数を求めてみましょう.

 

 　{ \displaystyle f'(x) = 3x^{2}-5 } であり,

 

{ \displaystyle f(x) = f'(x)q_{0}(x) - \dfrac{10}{3}x + 4 }

{ \displaystyle f'(x) = (-\dfrac{10}{3}x + 4)q_{1}(x) - \dfrac{17}{25} }

 

 ですから

 

 { \displaystyle r_{0}(x) = -\dfrac{10}{3}x + 4 }

{ \displaystyle r_{1}(x) = -\dfrac{17}{25} }

 

 となります, よってスツルム列は

 

{ \displaystyle f_{0}(x) = f(x) = x^{3}-5x+4 }

{ \displaystyle f_{1}(x) = f'(x) = 3x^{2}-5 }

{ \displaystyle f_{2}(x) = \dfrac{10}{3} - 4 }

{ \displaystyle f_{3}(x) = \dfrac{17}{25} }

 

 となります.

 

 　区間は { \displaystyle (0, 2) } だったので { \displaystyle x = 0, 2 } をそれぞれ代入し, 得た値の正負を書くと下のようになりますね.

 { \displaystyle f_{0} } { \displaystyle f_{1} } { \displaystyle f_{2} }{ \displaystyle f_{3} }  { \displaystyle V }
{ \displaystyle x=0 } { \displaystyle + } { \displaystyle - } { \displaystyle - } { \displaystyle + } { \displaystyle 2 }
{ \displaystyle x=2 } { \displaystyle + } { \displaystyle + } { \displaystyle + } { \displaystyle + } { \displaystyle 0 }

 

 　よって { \displaystyle V(0) = 2, V(2) = 0 } となるので, 実数解の個数 { \displaystyle N } は { \displaystyle 2-0 = 2 } となります.

 

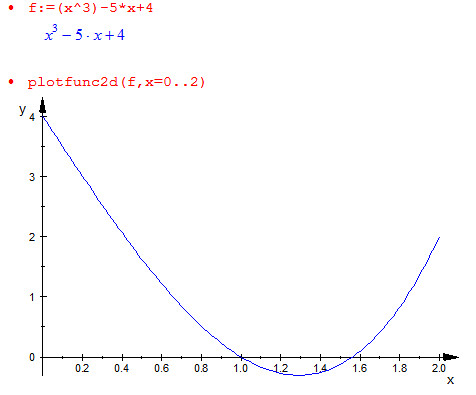
 130524_04

 　実際にグラフを見てみると, 確かに区間 { \displaystyle (0, 2) } 内で2点がx軸と交わっているのが分かります.

 

 

〆

 　マークシート方式ならともかく, 筆記などでは当然使えません.

 　余裕があったら試してみてください.

thetheorier