もう一人のY君

iPhoneアプリのレビューやアップデートレビューなどを書いています. たまに数学の記事も書きます.

もう一人のY君　MENU 　MENU

(数学)一つの原始根から残りの原始根を求める

数学

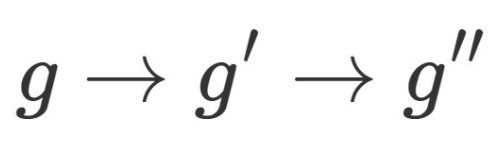
161015_09

　以前, 原始根の話をしましたが今回はその続きです.

 

thetheorier.hatenablog.com

 

[Contents]
 

 

原始根(復習)

　例によって再び原始根の定義だけ書いておきます.

 

[定義：原始根]

　素数 { \displaystyle p } と, { \displaystyle p } で割り切れない整数 { \displaystyle a } について, { \displaystyle a } が指数 { \displaystyle p-1 } に対応するとき, つまり { \displaystyle p-1 } よりも小さな正指数で { \displaystyle a^{e}\equiv 1\pmod p } とならないとき, { \displaystyle a } を { \displaystyle p } の原始根と呼ぶ.

 

 

その他の原始根を見つける

　素数 { \displaystyle p } によっては, たくさんの (実際には { \displaystyle \varphi(p-1) 個の })素数があるわけですが,  { \displaystyle p } が小さいうちは　{ \displaystyle 2 } から地道にやっても何とかなるものの, 大きくなるとそうはいきません.

 

　というわけで今回は,{ \displaystyle 1 }つ原始根 { \displaystyle g } を見つければ, これを用いて他の原始根も見つけられる…という理屈です.

 

 

[定理]

　素数 { \displaystyle p } とその原始根 { \displaystyle g } について, { \displaystyle g^a } がまた別の原始根であるための必要十分条件は

{ \displaystyle \text{gcd}(a, p-1)=1 }

となることである.

 

[定理の証明]

thetheorier.hatenablog.com

　先日のエントリにある補題2より, 素数 { \displaystyle p } の任意の原始根 { \displaystyle g } について

 

{ \displaystyle 1, g, g^2, \dots, g^{p-2} }

 

は規約代表です.

　つまりこれら { \displaystyle p-1 } 個は互いに素であるということです.

 

　もし { \displaystyle g^a } が { \displaystyle p } の原始根ならば, 上の規約代表の { \displaystyle g } を { \displaystyle g^a } に置き変えた

 

{ \displaystyle 1, g^a, g^{2a}, \dots, g^{(p-1)a}\tag{1} }

 

もまた規約代表です.

　また上記{ \displaystyle (1) }が規約代表である以上, { \displaystyle g } はこの { \displaystyle p-1 }個のいづれかであることも間違いありません.

　つまり { \displaystyle g } は法 { \displaystyle p } において { \displaystyle g^a } の累乗と等しいということです.

　よって合同式

 

{ \displaystyle g\equiv (g^a)^x \pmod p \\ \Leftrightarrow g\equiv g^{ax} \pmod p \\ \Leftrightarrow g^{ax-1}\equiv 1\pmod p\tag{2} }

 

は, 整数解 { \displaystyle x } を持ちます.

 

　ここで, 以下の補題を利用します.

[補題]

　素数 { \displaystyle p } について, { \displaystyle a^k\equiv 1\pmod p } が成り立つならば

{ \displaystyle k\equiv 0\,\left(\text{mod}{\,o(a)}\right) }

である.

　但し, { \displaystyle o(a) } は, { \displaystyle a^m\equiv 1\pmod p } を満たす最小の正指数のことである(この { \displaystyle o(a) } を位数と言う ).

 

[補題の証明]

{ \displaystyle k=q\cdot o(a)+r,\quad 0\leq r\lt o(a) }

を満たす整数 { \displaystyle q, r } を取ると,

 

{ \displaystyle a^k \\ \equiv a^{q\cdot o(a)+r} \\ \equiv \left( a^{o(a)}\right)^q \cdot a^r \\ \equiv a^r \\ \equiv 1 \pmod p }

 

　となるため, { \displaystyle a } は { \displaystyle k } より小さい数 { \displaystyle r } に対応します.

　しかし前回のエントリの補題1より, { \displaystyle a^h\equiv 1\pmod p } となる整数 { \displaystyle h } は { \displaystyle o(a) } の倍数に限られることを考えると { \displaystyle r } の定義から { \displaystyle r=0 } しかあり得ず, 従って

 

{ \displaystyle k=q\cdot o(a) }

 

, つまり

 

{ \displaystyle k\equiv 0\,\left(\text{mod}\,o(a)\right) }

 

となります. { \displaystyle \square }

 

　この補題より, { \displaystyle (2) } から

 

{ \displaystyle ax\equiv 1\,\left(\text{mod}\, p-1\right) }

 

が成り立ちます.

 

　1次合同式 { \displaystyle ax\equiv b\pmod m } が解を持つ必要十分条件は { \displaystyle \text{gcd}(a, m)=1 } であることですから, 今回であれば

 

{ \displaystyle \text{gcd}(a, p-1)=1 }

 

となります.

　逆については, 上の演繹を逆に辿れば十分です. { \displaystyle \square }

 

 

　この定理より, { \displaystyle p } の原始根 { \displaystyle g } を一つでも見つければ, { \displaystyle \text{gcd}(a, p-1)=1 } なる { \displaystyle a } における { \displaystyle g^a } も { \displaystyle p } の原始根…ということになるわけです.

 

 

実例

　例えば { \displaystyle p=19 } で試してみましょう.

 

thetheorier.hatenablog.com

　先日の数表から, { \displaystyle p=19 } の原始根は

 

{ \displaystyle 2, 3, 10, 13, 14, 15 }

 

の6個であることが分かります.

 

　ではまず { \displaystyle g=2 } が分かっているとしてその他を求めてみます.

 

　{ \displaystyle 19-1=18 } と互いに素な整数 { \displaystyle a\, (=1, 2, \dots 17) } は

 

{ \displaystyle 5, 7, 11, 13, 17 }

 

ですから,

 

{ \displaystyle 2^5, 2^7, 2^{11}, 2^{13}, 2^{17} }

 

も原始根であるはずです.

 

　計算してみると以下になります(法はいづれも{ \displaystyle 19 })

 

{ \displaystyle 2^5=16\times 2\equiv (-3)\cdot 2\equiv -6\equiv 13 }

{ \displaystyle 2^7\equiv (-6)\cdot 4\equiv -24\equiv 14 }

{ \displaystyle 2^{11}\equiv 14\cdot 16 \equiv (-5)\cdot (-3)\equiv 15 }

{ \displaystyle 2^{13}\equiv 15\cdot 4\equiv (-4)\cdot 4\equiv -16\equiv 3 }

{ \displaystyle 2^{17}\equiv 3\cdot 16\equiv 3\cdot (-3)\equiv -9\equiv 10 }

 

　見事にその他の原始根を網羅していますね.

 

　試しに他の原始根, 例えば { \displaystyle g=15 } を既知として他の原始根が導かれるか試してみましょう, { \displaystyle 15\equiv -4 } であることに注意すれば

 

{ \displaystyle 15^5\equiv (-4)^5\equiv 16^2\cdot (-4)\equiv 9\equiv (-4)\equiv -36\equiv 2 }

{ \displaystyle 15^7\equiv (15)^5\cdot (-4)^2 \equiv 2\cdot 16\equiv 32\equiv 13 }

{ \displaystyle 15^11\equiv (-6)\cdot (-4)^4\equiv (-6)\cdot (-3)^2 }  { \displaystyle \equiv -54\equiv 3 }

{ \displaystyle 15^13\equiv 3\cdot (-4)^2\equiv 48\equiv 10 }

{ \displaystyle 15^17\equiv (-9)\cdot (-4)^4\equiv (-9)\cdot 9\equiv -81\equiv 14 }

 

と, やはり全部求まりましたね.

 

 

〆

　他にもちょっとした原始根判定となるような定理もあります.

 

 

thetheorier