【数学】「震度6弱以上が30年以内に起きる確率」を考える

161231_02

　ちょくちょく聞かれる話ですね.

南海トラフ地震の予想される確率

　タイトルの通り, 「今後30年でマグニチュード8～9クラスの地震が起きる発生確率が70％」と言われています.

　70%と言えば中々の確率です, これを聞いて多くの人はそれなりに危機感を持つことでしょう.

　では実際, この数字がどの程度のものなのか, 考えてみたいと思います.

直近ではどのくらいの確率なのか

　この数字を見て, 「じゃあ1年後, 10年後はどうなのか」が気になる方もいると思います.

　これだけの情報でそれが具体的に分かるんでしょうか？ここで確率論の「確率分布関数」を用いて考えてみましょう.

確率分布関数

　確率空間 $(\Omega,\Sigma, P)$ と, この上で定義される確率変数 $X$ について,

$F_X(x):=P(X\leq x) = P((-\infty ,x])$

を確率分布関数と言います.

　一般的に, 分布関数は以下の性質を満たします.

$F_X(-\infty) = 0$
$F_X(\infty) = 1$
$F_X$ は非単調減少

　細かい話は抜きにして今回の例で言うならば, 「30年以内に起きる確率が70%」は

$P((-\infty ,30]) = 0.7$

と言えます.

　確率にはポアソン分布や二項分布などいくつかの特徴を備えたものがあり, 地震については「Brownian Passage Time」と呼ばれる分布に従っているそうですが, 例えば東海地震であればポアソン分布でも大きな違いは無いそうです.

161231_03

　今回は正確な値云々は議論しませんので, $X\gt 0$ , つまり既に起こった過去の場合は無視して考えましょう, つまり

$P(X\leq x) = P([0,x])$

を考えます.

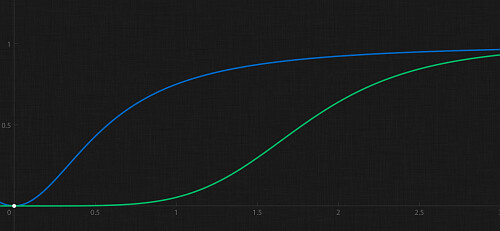
分関数が違うとどう変わるか

　分布関数には色んな形のものがあります.

　関数が違うことで他の「年」までの確率がどう変わるか, 2つの例を挙げて見てみます.

　話を戻して, 「30年までに起こる確率が70％」であることを条件にしてみます.

例1

　一つ目は次のような関数です.

$F_X(x) = \frac{7x}{7x+90}$

　 $F_X(30) = 7/10$ であることは直ちに分かりますね.

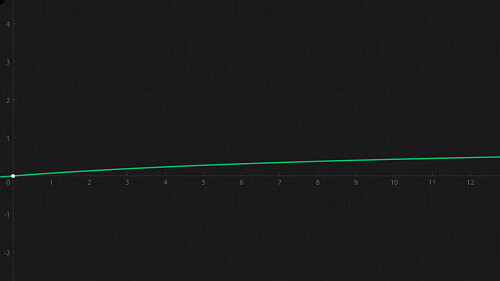
161231_06

　グラフの慨形は上の通りです.

　この場合の1年後, 5年後, 10年後, 20年後の確率を計算すると下のようになります.

$x$	$F_X(x)$
1	0.07216
5	0.28
10	0.04375
20	0.60870

　この場合, 1.43年後辺りで10%, 12.86年後辺りで確率が50%程度になります.

例2

　続いては以下の分布関数で試してみます.

　折角なのでかなり極端な関数になっています.

$F_X(x) = \frac{7x^{20}}{7x^{20}+10460353203\times 10^{20}}$

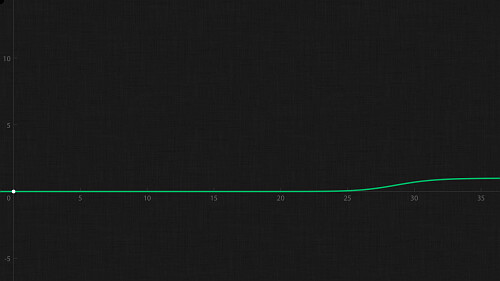
161231_07

　単純に見えて手計算はとても出来ない関数ですが, ちゃんと $P_X(30) = 0.7$ になります.

　この場合も1年後, 5年後, 10年後, 20年後の確率を計算してみると以下のようになります.

$x$	$F_X(x)$
1	6.69193×10^-30
5	6.38193×10^-16
10	6.69193×10^-10
20	7.01208×10^-4

　今回の場合, 20年後ですら0.7%に留まります.

　二つの分布関数で, 同じ1年後の確率でも前者は約7.2%, 後者は約6.7×10^-28%と, 天と地ほどの差があります.

　つまり, 「○○年内に△△%」という情報だけではそれ以上のことはハッキリ分からない…ということですね.

〆

　当然ですが, 地震というのはいつ, どこで, どの程度の大きさでやってくるのかを正確に知ることはできません.

　なのでこの結果を以て, そういう確率がまったくアテにならないというわけではありません.

もう一人のY君

主にiPhoneのショートカットアプリのレシピやTipsなどを書いています. たまに数学の記事も書きます.

【数学】「震度6弱以上が30年以内に起きる確率」を考える

南海トラフ地震の予想される確率

直近ではどのくらいの確率なのか

確率分布関数

分関数が違うとどう変わるか

例1

例2

〆