もう一人のY君

iPhoneアプリのレビューやアップデートレビューなどを書いています. たまに数学の記事も書きます.

もう一人のY君　MENU

【数学】連立一次合同方程式の解法

数学

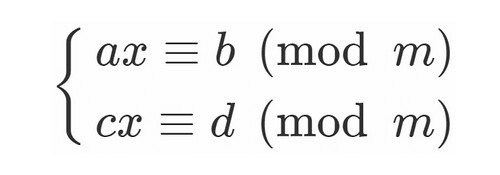
180216_01

　今回は連立一次合同方程式の解についてです.

 

スポンサーリンク

 

 

連立一次合同方程式を解く

　次の連立合同方程式を解くとします.

 

{ \displaystyle \left\{ \begin{array}{l} x\equiv a\pmod m \quad\dots (1) \\ x\equiv b\pmod n \quad\dots (2) \end{array} \right. }

 

　ここで { \displaystyle d:=\text{gcd}(m,n) } とします.

 

　(1)より, { \displaystyle x } は任意の整数 { \displaystyle k } を用いて

 

{ \displaystyle x=mk+a \quad\dots (3) }

 

と表せます.

 

　これは (2) を満たすので

 

{ \displaystyle mk+a\equiv b\pmod n \quad \dots (4) }

 

となります, つまり { \displaystyle mk+a-b } は { \displaystyle n } の倍数なので, 任意の整数 { \displaystyle k' } を用いて

 

{ \displaystyle mk+a-b=nk' \quad\dots (4') }

 

と表せます.

 

　ここで { \displaystyle mk, nk' } は共に { \displaystyle d=\text{gcd}(m,n) } を約数に持ちますから, { \displaystyle (4') } の左辺全体も { \displaystyle d } で割り切れることを考えると { \displaystyle a-b } も { \displaystyle d } で割り切れます, 従って (4) は法 { \displaystyle n':=\frac{n}{d} } において解を持ちます.

　これを

 

{ \displaystyle k\equiv k_0\pmod {n'} }

 

, つまり任意の整数 { \displaystyle s } を用いて

 

{ \displaystyle k=n's+k_0 }

 

とでもします.

 

　これを (3) に代入して

 

{ \displaystyle x }
{ \displaystyle = m(n's+k_0)+a }
{ \displaystyle = mn's + mk_0 + a }

 

, つまり { \displaystyle x - ( mk_0+a ) } が { \displaystyle mn'=\text{lcm}(m,n)=:l } の倍数ですから,

 

{ \displaystyle x\equiv mk_0+a\pmod l }

 

, これが解となります.

 

 

〆

　連立が3つ4つ…となる場合はこれを繰り返せば良い訳ですね.

 

thetheorier