もう一人のY君

iPhoneアプリのレビューやアップデートレビューなどを書いています. たまに数学の記事も書きます.

　MENU

【数学】2桁の自然数で正約数を最も多く持つ数

数学数学-問題

人気記事

Last modified：2017.06.14

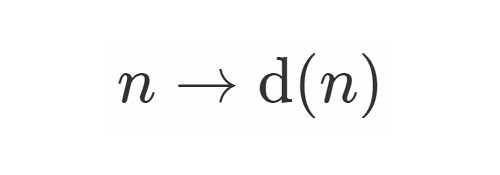
170612_00

　リクエストがあったのと某質問サイトで致命的なミスがあったのでここで改めて解説します.

スポンサーリンク

問題
〆
- 追記

問題

　2桁の自然数 $n$ のうち, 正約数を最も多く持つものを求めよ.

　なお, 以下については既知とします(今回の証明は割愛).

[補題1]

　 $2$ 以上の自然数は素因数分解によって一意的に表される.

　つまり自然数 $n (\geq 2)$ と対応する素数 $p, q, r, \dots$ および自然数 $a, b, c,\dots$ を用いて

$n = p^aq^br^c\dots$

[補題2]

　任意の自然数 $n(\geq 2)$ の正約数の個数 $\text{d}(n)$ は補題1の $p, q, r, a, b, c, \dots$ などを用いて

$\text{d}(n) = (a+1)(b+1)(c+1)\dots$

によって求まる.

問題の解答

　補題1により, 2以上の任意の自然数 $n$ は

$n = p^aq^br^c\dots$

という形に一意に素因数分解されます.

　また,

　

$2\times 3\times 5\times 7 = 210 \gt 100$

であることから2桁の自然数 $n$ は異なる高々3個の素因数によって構成されていることは明らかです.

　従って素因数が1～3個の場合を考えれば十分であることがわかります.

素因数が1個で構成されている場合)

　このとき対応する素数 $p$ と自然数 $a$ を用いて

$n = p^a$

$\text{d}(n) = a+1$

とできます.

　故に $\text{d}(n)$ が最大となるには $a$ が最大となれば良いことがわかります.

　これを満たすには

$n$ がより大きいこと
$p$ がより小さいこと

であれば良いことは明白です.

　従ってまず $p=2$ であれば良いことがわかります

　 $n$ は2桁なので $a$ は $10\leq 2^a\lt 100$ を満たす最大の自然数であれば良いです.

　 $64=2^6\lt 100 \lt 128 = 2^7$ なので $a=6$ が適応します.

　同じ理屈で $p=3$ のとき $a=4$ , $p=5$ のとき $a=2 \dots$ と真に小さくなり, $p=11$ 以降は明らかに $a=1$ なので今回の仮定を満たす $n$ は $n=2^6=64$ のただ一つであることがわかります.

　このとき $\text{d}(n)=6+1=7$ となります.

素因数が2個で構成されている場合

　このとき異なる素数 $p, q$ と自然数 $a, b$ を用いて

$n = p^aq^b$

$\text{d}(n) = (a+1)(b+1)$

とできます.

　先の場合と同じく, 素因数が大きすぎるとそれだけ指数が小さくなるため, $\text{d}(n)$ もまた小さくなります.

　まず最小の素数 $p=2$ を用いて得られる最大の $\text{d}(n)$ を考え, そこからそれを超える候補があるかどうかなどを考えます.

$2^5=32 \lt 2^6=64\lt 100$

であり, ここに $p=2$ に次ぐ最小の素数である $3$ を掛けると

$2^5\times 3=96 \lt 100\lt 2^6\times 3=192$

となります.

　従って $n=96=2^5\times 3$ のとき $\text{d}(n)=(5+1)(1+1)=12$ となります.

( $\text{d}(n)=12$ なる他の $n$ は存在するか)

　まずこの場合を考えます.

　 $n=p^5\times q$ という形で $p=2$ としたのが上記です.

　他にあるならば $p$ は少なくとも $2$ 以外の素数となります.

　その中で最小の組は $(p, q)=(3,5)$ ですが, このとき

$3^5\times 5 = 1215 \gt 100$

と, 2桁を大幅に上回ります.

　その他の組は言うまでもなくこれより更に大きいですから, 結果今回の仮定で $\text{d}(n)=12$ を満たす $(p, q)$ の組は $(2,3)$ のみであることがわかります.

( $\text{d}(n)=12$ に等しい, またはより大きい組み合わせは他に存在するか)

　次に $\text{d}(n)\geq 12$ となる $n$ が上の $p^5q^2$ 型以外に存在するかどうかを考えます.

　各々の素数のうち, $100$ を超えない最大の累乗を考えると,

$2^6=64\lt 100$

$3^4=81\lt 100$

$5^2=25\lt 100$

$7^2=49\lt 100$

$\dots$

であり, $p=11$ 以降は1乗止まりとなります.

　 $p^5q$ 型は上記で行った通りですから, それ以外で2桁となりうる, かつ $\text{d}(n)$ が $12$ 以上である組み合わせは上より

$p^4q^3,\, p^5q^2,\,p^3q^3,\,p^4q^2,\,p^3q^2$

の5種考えられます.

　各々の素数の組で最小のものである $(p, q)=(2,3)$ を代入すると,

$2^4\cdot 4^3=432\geq 100 \\ 2^5\cdot 3^2=288\geq 100 \\ 2^3\cdot 3^3=216\geq 100 \\ 2^4\cdot 3^2=144\geq 100 \\ 2^3\cdot 3^2=72\lt 100$

となり, 条件に合う組み合わせとして $n=2^3\cdot 3^2=72,\,\text{d}(72)=12$ が加わりました.

　最小の組は以上のため, これを除く組み合わせで2桁に収まるとしたら $n=3^3\cdot 5^2$ ですが, これは明らかに2桁ではありません.

　以上より, 条件を満たす $n$ として $n=96$ の場合と結果が等しい $n=72$ が得られました.

　以上より, 異なる素因数が2個の場合

$n=72, 96,\, \text{d}(n)=12$

が最大であることが分かりました.

　この時点で $7\lt 12$ であるため, 素因数が1個の場合で得られた $n=64$ は不適となります.

素因数が3個で構成されている場合

　このとき異なる素数 $p, q, r$ と自然数 $a, b, c$ を用いて

$n = p^aq^br^c$

$\text{d}(n) = (a+1)(b+1)(c+1)$

とできます.

　この場合, $3\times 5\times 7=105\lt 100$ であることから, 候補となる素因数の組は $(p,q,r)=(2,3,5), (2,3,7)$ のみであることが直ちにわかります.

　加えて $2\times 3\times 5=30,\, 2\times 3\times 7 = 42$ ですからここから更に素数を掛けて2桁にとどまるのは

$2^2\times 3\times 5 = 60 \\ 2^2\times 3\times 7 = 84 \\ 2\times 3^2\times 5 = 90$

の3組しかありません.

　このとき

$\text{d}(2^2\times 3\times 5) = 12 \\ \text{d}(2^2\times 3\times 7) = 12 \\ \text{d}(2\times 3^2\times 5) = 12$

ですから現時点での最大である $n=72, 96$ の場合に等しいです.

　以上より, 求める自然数 $n$ は $n= 60, 72, 84, 90, 96$ で, $\text{d}(n)=12$ となります. $\square$

〆

　丁寧に書いたら想像以上に長くなってしまいました.

追記

　 $n=84$ (素因数が3個の場合)を失念していました.