もう一人のY君

iPhoneアプリのレビューやアップデートレビューなどを書いています. たまに数学の記事も書きます.

もう一人のY君　MENU 　MENU

(数学コラム)素数が無限に存在することの証明

数学

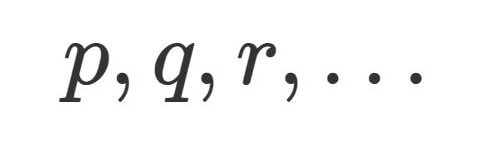
161105_13

　今回は素数が無限に存在する証明についてです.

 

[Contents]
 

 

よくある背理法

　学校でも学ぶ証明法の一つとして, 背理法を用いた証明がありますね.

　実際に書いてみると以下になります.

 

 

[定理]

　素数は無限に存在する.

 

[定理の証明1]

　素数が有限個しか存在しないと仮定します.

　それらの素数を

 

{ \displaystyle p_1, p_2, \dots, p_n }

 

とします.

 

　ここで以下の数を考えます.

 

{ \displaystyle M_n:=p_1\times p_2\times\dots\times p_n+1 }

 

　{ \displaystyle M_n } は自然数であることは間違いありませんから, 素数であるか合成数であるかのどちらかなのもまた自明です.

　従って素数であるか合成数であるかによって場合分けして考えます.

 

[{ \displaystyle M_n } が素数のとき]

　このとき, { \displaystyle M_n } は如何なる素数 { \displaystyle  p_k\, (k\in \{1, 2, \dots n\})} とも異なる数ですから, 最初に仮定した { \displaystyle n } 個の素数と異なる素数を認めることになります.

　従って { \displaystyle M_n } は素数ではありません.

 

[{ \displaystyle M_n } が合成数のとき]

　このとき, { \displaystyle M_n } は最初に仮定した { \displaystyle n } 個の素数の少なくとも一つを割りきるはずです.

　しかし任意の { \displaystyle p_k\, (k\in \{1, 2, \dots ,n\}) } で割っても必ず { \displaystyle 1 } 余りますから, { \displaystyle M_n } は合成数ではあり得ません.

 

　以上より, { \displaystyle M_n } が素数であると仮定しても, 合成数と仮定しても矛盾が生じるため, 最初の仮定である「素数が有限個しかない」が間違っていることになります.

 

　よって背理法により素数は無限個存在することがわかります. { \displaystyle \square }

 

　因みに素数 { \displaystyle p_1, p_2, \dots ,p_n } は小さい順に並べる必要は特にありません.

 

 

ユークリッド原論での証明

　よくある誤解が, 上記が「ユークリッド原論にある証明法だ」ということです.

　確かによく似ているのですが背理法でないという意味でも明確に異なります.

　実際に見てみましょう.

 

 

[定理の証明2]

　任意の異なる { \displaystyle n } 個の素数

 

{ \displaystyle p_1, p_2, \dots , p_n }

 

のリストを与え, これを用いて次の数を定めます.

 

{ \displaystyle M_n:=p_1\times p_2\times\dots\times p_n+1 }

 

　これは素数であるか合成数であるかは証明1同様明らかです.

 

[{ \displaystyle M_n } が素数のとき]

　このとき, 明らかに任意の { \displaystyle k\,(k=1, 2, \dots ,n) } について { \displaystyle M_n\gt p_k } ですから, リストに無い新しい素数 { \displaystyle M_n } が構成されたことになります.

 

[{ \displaystyle M_n } が合成数のとき]

　このとき, 如何なる { \displaystyle p_k\, (k=1, 2, \dots ,n) } についても { \displaystyle M_n } は { \displaystyle p_k } を割りきらないため, リストにない別の素数が存在することを意味します.

 

　以上より, { \displaystyle M_n } が素数であるか合成数であるかに関わらず, リストにない新しい素数が存在することが分かります.

 

　リストは任意に作ったので, 新しい素数はいくらでも作ることができることを意味します. { \displaystyle \square }

 

 

スポンサーリンク

 

二つの証明の違い

　いづれも { \displaystyle M_n:=p1\times p_2\times\dots\times p_n+1 } という数を用い, またこれが素数であるか合成数であるかによって場合分けしているわけですが, 言論での証明法は明らかに背理法ではありません.

 

　原論で主張していることは「どんなリストからも, そこにない素数を作り出すことができる」と言っているだけですからね.

 

　また後者の証明は, 見ての通りで { \displaystyle M_n } が必ずしも新しい素数だとは言っていません.

 

　例えばリスト { \displaystyle \{2,3,5,7,11,13\} } に対して

 

{ \displaystyle 2\times 3\times 5\times 7\times 11\times 13 +1\\=30031 = 59\times 509 }

 

　ですから, このとき { \displaystyle M_n } は明らかに素数ではありませんがリストにない素数 { \displaystyle 59, 509 } が確かめられます.

 

　証明1は飽くまでも各々の仮定の矛盾を示すために用いたわけです.

 

 

〆

　注意してほしいのは, だからといって証明1が間違っているということではありません.

 

　ほとんど同じように見えるこの2つの証明は互いに別証明…ということですね.

 

 

thetheorier