もう一人のY君

iPhoneアプリのレビューやアップデートレビューなどを書いています. たまに数学の記事も書きます.

もう一人のY君　MENU 　MENU

(数学)代数系の一覧

数学

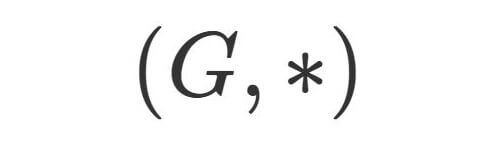
161004_14

　今回は代数学での基本, 代数系を一通り紹介したいと思います.

 

[Contents]
 

 

代数系とは

　我々は当たり前に, 例えば自然数や実数について四則演算を行っていますが, 代数学ではこれを抽象化し, その構造自体を研究します.

 

　当然日常で使っている四則演算などが元になっているわけですが, より深く学んでいくとより抽象化されて分かりにくくなるのは数学の運命ですね.

 

　その辺はともかく, 代数系とは簡単に言えば(主に)数を対象とする集まりに演算という「構造」を入れる, 或いは入れた構造によって全体が, 個がどのように変化するのかを考えます.

　従って四則演算が使えるという常識は必ずしも通用しません.

　むしろ「どんな代数系にはどの演算が適用できるのか」と考えたくなるようになります.

 

 

色んな代数系

　代数系は(基本的なものに限り)大きく2種類に分かれ, 後述する「二項演算」が1つの場合と2つの場合に分かれます. 

 

亜群(マグマ)

　空でない集合 { \displaystyle G } による直積 { \displaystyle G\times G } から { \displaystyle G } への写像

{ \displaystyle G\times G\to G \\ \displaystyle (a,b)\mapsto c(=a*b) }

を定めることができるとき, 結合三法 { \displaystyle * } を { \displaystyle G } の二項演算, { \displaystyle c } を { \displaystyle a, b } の「積」と呼ぶ.

　またこのとき, 「{ \displaystyle G } は二項演算 { \displaystyle * } について「閉じている」, 「閉鎖律をなす」, 「{ \displaystyle (G, *) } は亜群(groupoid), またはマグマ(magma)である」と言う.

　ここに挙げた { \displaystyle * } は掛け算でなく, 四則演算を含めたより抽象的な意味です.

　またここで挙げた「積」も同様で掛け算の意味ではありません.

　参考書によって亜群と読んだりマグマと読んだり様々です.

 

　以降, 問題の無い範囲で { \displaystyle (G, *) } などとするべきところをしばしば { \displaystyle G } と簡約することがあります.

　つまり, 我々が自然数や実数などと言うとき, 無意識に二項演算を含めて言及していたり, 単純に数の集まりとして言及していたりするわけです.

　これは代数系に限らず位相空間など, 数学の多くの分野で自然と「省略」しています.

 

　いずれにしろこの亜群は, とにかく { \displaystyle G } から取った任意の元による二項演算の結果が再び { \displaystyle G } の元でさえあれば良い事になります.

　代数系でもっとも原始的と言えましょう.

 

　しかし例えば { \displaystyle (\mathbb{N, -}) } のように, 亜群ですらない代数系もたくさん考えられます.

　なぜこれが亜群でないかは簡単に分かると思います.

 

　逆に四則演算ですらなくとも例えば

{ \displaystyle a*b := a+b-1 }
(右辺の{ \displaystyle +,- }は通常の加法、減法)

として二項演算を定めた代数系 { \displaystyle (\mathbb{Z}, *) } は亜群になりますね.

 

　以降, { \displaystyle (G,*) } などとすべきところを { \displaystyle G } と省略します.

 

 

半群

　亜群 { \displaystyle G } が以下の結合律を満たすとき, { \displaystyle G } を半群(semi-group)と言う.

　{ \displaystyle G } の任意の元 { \displaystyle a,b,c } に対して,

{ \displaystyle (a*b)*c = a*(b*c) }.

 

 

単位的半群(モノイド)

　半群 { \displaystyle G } の任意の元 { \displaystyle a } について,

{ \displaystyle e*a=a*e=a }

を満たすような { \displaystyle G } の元 { \displaystyle e } がただ一つ存在するとき, { \displaystyle G } を単位的半群(unitary semigroup), 或いはモノイド(monoid)と呼び, { \displaystyle e } を { \displaystyle G } の単位元と言う.

　この単位元を{ \displaystyle 0 }, あるいは{ \displaystyle 1 }と決めつけたくなりますが, 残念ながら代数系によってはそのどちらでもありません.

　例えば先程挙げた

{ \displaystyle (\mathbb{Z}, *)\quad a*b:=a+b-1 }

, これはモノイドですが単位元は{ \displaystyle 0 }でも{ \displaystyle 1 }でもなく{ \displaystyle -1 } になります.

　従って, 単位元を

{ \displaystyle 0_G }

と書くこともあります.

 

　誤解を与えぬよう, { \displaystyle \mathbb{N} := \{ 1, 2, 3,\dots \} } としましょう.

　これに一般的な加法 { \displaystyle + } を入れた { \displaystyle (\mathbb{N}, +) } はモノイドでしょうか？

　残念ながら違いますね.

　{ \displaystyle 0\notin\mathbb{N} } であるため, 単位元が存在しないからです.

 

　このように, 高校数学以下を含め一般的に自然数に{ \displaystyle 0 } は含めませんが, 含めた方が都合がよい場合が往々にして存在します.

 

 

群

　モノイド { \displaystyle G } について, 任意の { \displaystyle G } の元 { \displaystyle a } に対して

{ \displaystyle a*a'=a'*a=e }
({ \displaystyle e }は{ \displaystyle G }の単位元)

を満たす { \displaystyle G } の元 { \displaystyle a' } が, { \displaystyle a } に応じてただ一つずつ存在するとき, { \displaystyle G } を群(group)と呼び, { \displaystyle a' } を({ \displaystyle a }の)逆元と言う.

　群は非常に研究しがいのあるカテゴリの一つであり, 方程式論やガロア理論, 図形(移動, 回転)などに深く関わっています.

 

 

可換群(アーベル群)

　群 { \displaystyle G } が可換律を満たす, つまり { \displaystyle G } の任意の元 { \displaystyle a, b } に対して

{ \displaystyle a*b=b*a }

を満たすとき, { \displaystyle G } を可換群(commutative group), 或いはアーベル群(abelian group)と言う.

　参考書によっては, このアーベル群を群として定義する場合があります.

 

 

加法群, 乗法群

　二項演算 { \displaystyle * } が加法であるアーベル群を加法群(additive group), 同じく乗法である群(こちらはアーベル群であることを要しない)を乗法群(multiplicative group)と呼ぶ.

　加法群では, 単位元 { \displaystyle e } を特別に「零元」と呼び { \displaystyle 0(\equiv 0_G) } と書き, また逆元は「反元」と呼び, { \displaystyle a } に対して { \displaystyle -a } と書きます.

　この { \displaystyle -a } についた { \displaystyle - } は結合三法でないことに注意です.

　例えば { \displaystyle 1-(-2) } という式にある二つの { \displaystyle - } は, 厳密に言えば別物ということですね.

　また乗法群において, { \displaystyle G } の任意の元 { \displaystyle a } に対応する逆元を { \displaystyle a^{-1} } と書き表します.

　こちらも厳密には指数 { \displaystyle a^{-1} } とは別物ですが, 指数と同一視して扱うことが可能です.

 

 

　亜群から群に至る流れは基本的に以上ですが, 別の流れとして以下の「準群」「擬群」が存在します.

 

 

準群

　空でない亜群 { \displaystyle G } について, 任意の { \displaystyle a, b\in G } に対して

{ \displaystyle ax=b }

を満たす元 { \displaystyle x } が { \displaystyle G } に属するとき, { \displaystyle G } を準群(quasi group)と呼ぶ.

　簡単に言えば「常に割り算ができる」代数系です.

 

 

擬群

　準群 { \displaystyle G } が単位元を持つとき, 擬群(Loop)と呼ぶ.

 

　そして, 擬群の中でも結合律を持ったものは群となります.

 

　つまり,

 

 亜群
{ \displaystyle \xrightarrow{結合律} }半群
{ \displaystyle \xrightarrow{単位元の存在} }モノイド
{ \displaystyle \xrightarrow{逆元の存在} }群

という流れと

 

 亜群
{ \displaystyle \xrightarrow{除法が可能(消約性)} }準群
{ \displaystyle \xrightarrow{単位元の存在} }擬群
{ \displaystyle \xrightarrow{結合律} }群

の2通りがあるわけですね.

 

 

環

　ここから二項演算が2つになります.

 

　加法群 { \displaystyle R } に次のような乗法 { \displaystyle ab (=a\times b) } が定義されるとき, { \displaystyle R } は環(ring)を成すという.

  1. 乗法 { \displaystyle \times } は結合律を満たす { \displaystyle \bigl( \Leftrightarrow (R,*) } が半群を成す { \displaystyle \bigr) }
  2. 加法と乗法との間に次のような分配律が成り立つ.

{ \displaystyle a\times (b+c)=ab+ac\\ (a+b)\times c=ac+bc }

 

　特に環 { \displaystyle \{ 0\} } は零環と呼ばれます.

　零環は環としては余りにもトリビアルであるため, これを除いて, つまり { \displaystyle R\neq\{0\} } について定義する参考書もあります.

 

 

単位的環

　環 { \displaystyle R\neq\{ 0\} } が, { \displaystyle 0 } でない乗法単位元を持つとき, { \displaystyle R } を単位的環(unitary ring)と呼ぶ.

 

　参考書によっては, この単位的環を環と定義することがあります.

 

 

正則、可逆

　単位的環 { \displaystyle R } の任意の元 { \displaystyle a } に対して

{ \displaystyle aa'=a'a=e }
({ \displaystyle e }は{ \displaystyle R }の乗法単位元)

を満たす { \displaystyle R } の元 { \displaystyle a' } が存在するとき, { \displaystyle a } は正則(non-singular), 或いは可逆(invertible)であると言い, { \displaystyle a' } を { \displaystyle a } の可逆元(invertible element)と言う.

 

　先程の逆元のくだりとそっくりなのに呼び名が若干違いますが仕方ないですね…

　因みに「正則」という言葉は他の分野でも, やや表現を変えて出てくるのでこちらもまた厄介です.

 

 

環から生成される乗法群

　単位的環 { \displaystyle R } の正則な元をすべて集めた集合は乗法に関して群を成す.

　これを { \displaystyle R^\times } と表し, { \displaystyle R } の乗法群と呼ぶ.

 

 

可換環

　環 { \displaystyle R } が乗法に関して可換律を満たすとき, { \displaystyle R } を可換環(commutative ring)と言う.

 

　ここでは飽くまでも「環」であり, 従って乗法単位元の存在は要求していないことに注意です.

 

 

整域

　可換環 { \displaystyle R } が零因子を持たないとき, { \displaystyle R } を整域(integral domain)と言う.

 

　名前から察せられる通り, 整域の例として整数(環)が挙げられます.

　零因子とは, { \displaystyle 0 } でない { \displaystyle R } の元 { \displaystyle a } であって

{ \displaystyle ab=0 }, 或いは { \displaystyle ba=0 } を満たす { \displaystyle b\in R } が存在する

ものを言います.

　逆に「零因子を持たない」とは以下が成り立つことを言います.

{ \displaystyle ab=0\Rightarrow a=0\vee b=0 }

 

 

　ここから先は「環」でなく「体」という代数系に傾倒した代数系となります. 

 

斜体

　単位的環 { \displaystyle F } の任意の元 { \displaystyle a\neq 0 } が正則であるとき, { \displaystyle F } は斜体(skew field), 或いは非可換体(non-commutative field)と言う.

 

　後述する体との違いとしては以下が挙げられます.

 

[非可換性]

　乗法に関して, { \displaystyle F } の元 { \displaystyle x, y } であって

{ \displaystyle xy\neq yx }

であるものが存在する.

 

[可除性]

　{ \displaystyle F } の零元でない元 { \displaystyle x } に対して, その乗法逆元 { \displaystyle x^{-1} } が必ず存在する.

 

　代数系が斜体となってはじめて環という枠で除法が自由にできるようになるため, これを強調して「可除環(division ring)」と呼ぶこともあるそうです.

 

 

体

　斜体 { \displaystyle F } が乗法において可換律を満たすとき, { \displaystyle F } を体(field)と呼ぶ.

 

　この体が環の終着点の一つなわけですが, 残念ながら体であっても0除算は不可能です.

　明らかに

{ \displaystyle 0\times x = x\times 0 = 1_F }

なる { \displaystyle x } は存在しないからです.

 

　よって一般的に「{ \displaystyle 0 }で割ることを除いて」四則演算が可能…となります.

 

 

減法、除法の定義

　代数学において, 基本となる演算は上の通りで加法と乗法です.

　減法, 除法はこれらが定義されてから定めることが可能となり, 具体的には

 { \displaystyle a-b:=a+(-b) \\ a/b:=a\times b^{-1} }

として定義されます.

 

 

thetheorier