もう一人のY君

iPhoneアプリのレビューやアップデートレビューなどを書いています. たまに数学の記事も書きます.

もう一人のY君　MENU 　MENU

【数学】有限集合から実際に加法族を作ってみる

数学

σ-加法族

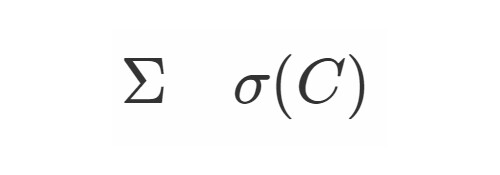
　今回は与えられた集合系からσ-加法族を作ってみたいと思います.

 

スポンサーリンク

 

 

有限集合から加法族を作る

blog.thetheorier.com

　加法族の定義については以前も書きましたがここでも書いておきます.

 

 

[定義1：加法族]

　集合 { \displaystyle S } の部分集合による系 { \displaystyle \Sigma_0 } が以下を満たすとき, { \displaystyle \Sigma_0 } を({ \displaystyle S } 上の)加法族と言います.

 

  1. { \displaystyle S\in\Sigma_0 }
  2. { \displaystyle F\in\Sigma_0\quad \Rightarrow\quad F^c:=S\backslash F\in\Sigma_0  }
  3. { \displaystyle F, G\in\Sigma_0\quad\Rightarrow\quad F\cup G\in\Sigma_0 }

 

　加法族の定義から, 各々は次に置き換えられることもすぐにわかります.

 

　1-1. { \displaystyle \emptyset\in\Sigma_0 }

　3-1. { \displaystyle F, G\in\Sigma_0\quad\Rightarrow F\cap G\in\Sigma_0 }

　3-2. { \displaystyle F, G\in\Sigma_0\quad\Rightarrow F\cup G^c\in\Sigma_0 }

　3-3. { \displaystyle F, G\in\Sigma_0\quad\Rightarrow F^c\cup G\in\Sigma_0 }

　3-4. { \displaystyle F, G\in\Sigma_0\quad\Rightarrow F\cap G^c\in\Sigma_0 }

　3-5. { \displaystyle F, G\in\Sigma_0\quad\Rightarrow F^c\cap G\in\Sigma_0 }

 

 

[定義2：σ-加法族]

　集合 { \displaystyle S } の部分集合による系 { \displaystyle \Sigma } は { \displaystyle S } 上の加法族であり, かつ任意の集合列 { \displaystyle F_n\in\Sigma,\ (n\in\mathbb{N}) } について常に

 

{ \displaystyle \bigcup_{n\in\mathbb{N}}F_n\in\Sigma }

 

が成り立つとき, { \displaystyle \Sigma } を { \displaystyle S } 上のσ-加法族と言います.

 

　実際には, 例えば要素数n個の有限集合のすべての部分集合からなる族の要素が { \displaystyle 2^n } 個であるように, 高々有限個の集合であってもそのσ-加法族はおろか加法族を具体的に書き表すのも大変どころか非現実的です.

 

　従って今回取り上げるのは { \displaystyle S } が有限集合であるということです.

 

　因みに, もっとも小さな(σ-)加法族が { \displaystyle \{\emptyset, S\} } であることは明白です.

 

 

σ(C)

　集合 { \displaystyle S } の部分集合によるクラス(類) { \displaystyle \mathcal{C} } が与えられているとき, { \displaystyle \mathcal{C} } を含む最小のσ-加法族のことを { \displaystyle \sigma({\mathcal{C}}) } と書き表します.

 

　定義上は集合系でなく「クラス」になりますが, 今回はもうちょっと「柔らかい」解釈で使用します.

 

 

指定した集合系を含むσ-加法族を作ってみる

　さて本題に入ります.

　σ-加法族と書いてますが実際には有限集合を扱うので実際は加法族の定義を満たしていれば十分です.

 

　まず例として { \displaystyle S=\{1, 2, 3, 4\} }, { \displaystyle \mathcal{C}=\{\{1\},\{1,4\}\} } を挙げてみます.

 

 

step:1
{ \displaystyle F } { \displaystyle F^c } 
{ \displaystyle \{1,2,3,4\} }  { \displaystyle \emptyset } 

 

　書き方は色々でしょうが, 今回は上のように { \displaystyle \sigma (\mathcal{C}) } となるような要素を書き下していきます.

　この際左右に振り分け, 一方が他方の補集合であるようにします.

　こうすることで加法族の定義2を常に漏らすことなく得られます.

　まず手始めに { \displaystyle S } 自身を, となると加法族の定義2より { \displaystyle S\backslash S=\emptyset } も要素ですから右に書きます.

 

 

step:2
{ \displaystyle F } { \displaystyle F^c } 
{ \displaystyle \{1,2,3,4\} }  { \displaystyle \emptyset } 
{ \displaystyle \{1\} }  { \displaystyle \{2,3,4\} } 

 

　続いて { \displaystyle \mathcal{C} } の要素の一つである { \displaystyle \{1,4\} } を { \displaystyle F } の次の列に追加します.

　{ \displaystyle \{1\} } の補集合である { \displaystyle \{2,3,4\} } も忘れずに追加します.

 

 

 

{ \displaystyle F } { \displaystyle F^c } 
{ \displaystyle \{1,2,3,4\} }  { \displaystyle \emptyset } 
{ \displaystyle \{1\} }  { \displaystyle \{2,3,4\} } 
{ \displaystyle \{1,4\} }  { \displaystyle \{2,3\} } 

 

　同じように { \displaystyle \{1\} } に関わる集合も追加します.

 

 

step3
{ \displaystyle F } { \displaystyle F^c } 
{ \displaystyle \{1,2,3,4\} }  { \displaystyle \emptyset } 
{ \displaystyle \{1\} }  { \displaystyle \{2,3,4\} } 
{ \displaystyle \{1,4\} }  { \displaystyle \{2,3\} } 
{ \displaystyle \{1,2,3\} }  { \displaystyle \{4\} } 

 

　追加済の要素を用いた集合演算によって異なる集合を得られるならば, これを追加します.

 

[ヒント]

　追加前の各要素の組み合わせはすべて列挙されているはずですから, ここで考える組み合わせは「追加した要素或いはその補集合」と「追加前の各要素」に絞られることがわかります.

　また対象の集合の補集合も列挙していますから, 考える集合演算は和集合・共通部分どちらか一方で済みます.

　和集合なら追加した集合そのもの(表の左側), 共通部分なら同じく右側のみ考えれば大丈夫です.

 

　今回は { \displaystyle \{1\} }, { \displaystyle \{2,3\} } を用いて { \displaystyle \{1,2,3\} } を作れるのでこれを追加します.

 

　以下step2とstep3を繰り返し, 漏れがなければすべての要素が書き出されるということになります.

 

　step2では { \displaystyle \mathcal{C} } の要素を, step3ではそれまで追加したものの集合演算で作れる新しい集合を追加していくわけです.

 

　今回の場合, つまり { \displaystyle \sigma(\mathcal{\{ 1 \}, \{1,4\}}) } の要素は

 

{ \displaystyle \emptyset \\ \{1\} \\ \{4\} \\ \{1,4\} \\ \{2,3\} \\ \{1,2,3\} \\ \{2,3,4\} \\ \{1,2,3,4\} }

 

の8個になります.

 

 

〆

　この方法だと, 要素を追加してもその続きからどんどんリストを追加することができます.

 

　上の例では { \displaystyle \mathcal{C}=\{\{1\},\{1,4\}\} } でしたが, ここから更に例えば { \displaystyle \{2\} } を追加する場合, 最後の表から続けて { \displaystyle \{2\} } を追加し, step2, step3を繰り返せば良いわけです.

 

 

{ \displaystyle F } { \displaystyle F^c } 
{ \displaystyle \{1,2,3,4\} }  { \displaystyle \emptyset } 
{ \displaystyle \{1\} }  { \displaystyle \{2,3,4\} } 
{ \displaystyle \{1,4\} }  { \displaystyle \{2,3\} } 
{ \displaystyle \{1,2,3\} }  { \displaystyle \{4\} } 
{ \displaystyle \{2\} }  { \displaystyle \{1,3,4\} } 
{ \displaystyle \{1,2\} }  { \displaystyle \{3,4\} } 

 

　何となく分かったでしょうか？

 

 

 

 

 

 

 

 

 

 

 

thetheorier