もう一人のY君

iPhoneアプリのレビューやアップデートレビューなどを書いています. たまに数学の記事も書きます.

もう一人のY君　MENU 　MENU

(数学)合同式の有理数表示

数学

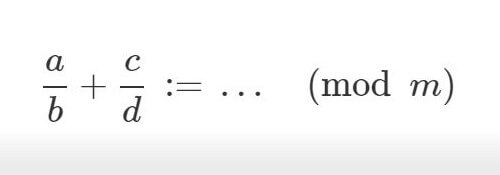
161120_17

　高校数学から取り上げられる合同式ですが, うまいこと定めれば有理数をそのままあてはめて使うことが可能です.

 

 

一次合同方程式の解について

　順に追ってみましょう.

 

　まず一次合同方程式 { \displaystyle ax\equiv b\pmod m } は, { \displaystyle \text{gcd}(a,m)=1 } であるときただ一つの解を持ちますね.

 

　まずこの事実から説明しておきましょう.

 

　{ \displaystyle x } による { \displaystyle m } を法とした剰余系

 

{ \displaystyle x_1, x_2,\dots, x_m }

 

を与えると, 各々の値に { \displaystyle a } をかけた

 

{ \displaystyle ax_1, ax_2,\dots, ax_m }

 

もまた剰余系のひとつです.

 

　仮にそうでない, つまりこの剰余系のうちの2つについて { \displaystyle ax_s\equiv ax_t \pmod m } であると仮定します.

　これを満たすのは合同式の定義から { \displaystyle ax_s-ax_t = a(x_s-x_t) } が { \displaystyle m } の倍数であるということですが, { \displaystyle \text{gcd}(a,m)=1 } でしたから { \displaystyle x_s-x_t } が { \displaystyle m } の倍数であるということになります.

　しかしこれは { \displaystyle x_s\equiv x_t } ということになり, 仮定に反します, よって一つの剰余系において互いに合同である2数は存在しません.

 

　従って任意の整数 { \displaystyle b } について

 

{ \displaystyle ax\equiv b \pmod m }

 

となるような { \displaystyle x } が, 上記の剰余系の中にただひとつ存在します.

 

　これが一次合同式の解の存在証明の一部です.

　{ \displaystyle \text{gcd}(a,m)\gt 1 } である場合は解の個数が2つ以上存在することになりますが, 今回はその事実のみ指摘し, 証明は割愛します.

 

　以下, 引き続き合同式 { \displaystyle ax\equiv b \pmod m } として話を進めます.

 

 

合同式における有理数表示

　{ \displaystyle \text{gcd}(a,m)=1 } である場合に限り, 合同方程式 { \displaystyle ax\equiv b \pmod m } はただ一つの解を持ちますから, ここから一般的な方程式の要領で有理数 { \displaystyle \frac{b}{a} } を表現できそうです.

 

　即ち, 合同方程式 { \displaystyle ax\equiv b \pmod m } が { \displaystyle \text{gcd}(a,m)=1 } であるとき, この解を以て法 { \displaystyle m } における有理数として { \displaystyle \frac{b}{a} } を定義するのです.

 

　しかし, これだけで定義が正しいのかは分かりません.

　つまりこれが有理数相当の定義を満たすのか…という問題があります.

　ここは清く, 然るべき定義を満たしているか順に確認することにしましょう.

 

 

blog.thetheorier.com

　流れとしては大まかにこちらに従います.

 

 

演算の定義(亜群)

　まず演算を定義しましょう, そして結果的にこれを含めた代数系が有理数と同じ振る舞いをするのか, 有理数と同じ「体」であるかを確認しましょう.

　また前述によって得られた集合を { \displaystyle M } とでもしておきましょう.

 

{ \displaystyle M:=\{ \frac{a}{b} | bx\equiv a \pmod m, \text{gcd}(b,m)=1 \} }

 

　先程と記号が違うので注意してください.

　なお以降は必要でない限り法の表記は省略します.

　更に, 然るべき任意の整数 { \displaystyle a,b,c,d,e,f } を予め定めておきます, つまり

 

{ \displaystyle ax\equiv b \\ cx\equiv d \\ ex\equiv f }

 

 

　さて, (二項)演算ですがこれは有理数と同一視できる上, 高木貞治著の「初等整数論講義　第二版」p.34 に倣って以下で定義します.

 

〔注意〕{ \displaystyle (a,m)=1 } であるとき, { \displaystyle ax\equiv b \pmod m } の解は { \displaystyle \text{mod }m. } に関して一定であるから, それを { \displaystyle b/a } で表わすことがある.

　例えば { \displaystyle \frac{1}{2}\equiv 4\pmod 7 }, { \displaystyle \frac{2}{3}\equiv 5\pmod 13 }.

　このような記号に分数の計算法を適用することができる.

　例えば

 { \displaystyle \frac{a}{c}+\frac{c}{d} :\equiv \frac{ad+bc}{bd} }

{ \displaystyle \frac{a}{b}\times\frac{c}{d}:\equiv \frac{ac}{bd} }

 

[共立出版株式会社]初等整数論講義　第二版　高木貞治著：p.34

　著書ではこれが亜群であることをこの後に示しています. 

 

　この代数系 { \displaystyle (M,+,\times ) } が体であることを確認するのが今回の目的です.

 

　まずはこの定義によって { \displaystyle (M,+), (M,\times ) } が亜群であるかどうかを確かめます.

 

　{ \displaystyle x=\frac{a}{b}, y=\frac{c}{d} } と置くと, 定義より { \displaystyle \text{gcd}(b,m)=\text{gcd}(d,m)=1 } であり, また

 

{ \displaystyle bx\equiv a \\ dy\equiv c }

 

, よって

 

{ \displaystyle bd(x+y)\equiv bd(\frac{a}{b}+\frac{c}{d})\equiv ad+bc }

{ \displaystyle bcxy\equiv bd\times \frac{a}{b}\times\frac{c}{d} \equiv ac }

 

, 従って

 

{ \displaystyle x+y\equiv \frac{a}{b}+\frac{c}{d}\equiv \frac{ad+bc}{bd} }

{ \displaystyle xy\equiv \frac{a}{b}\times\frac{c}{d}\equiv \frac{ac}{bd} }

 

, この解は { \displaystyle \text{gcd}(b,m)=\text{gcd}(d,m)=1 } より { \displaystyle \text{gcd}(bd,m)=1 } なのでただ一通りに定まっています.

 

　よって { \displaystyle (M,+), (M,\times ) } 共に亜群であることがわかります.

 

 

スポンサーリンク

 

可換律

　続いて可換律です.

　本来結合律などを確かめるところですがこちらを先に証明しておいたほうが後が楽なので.

　合同式そのものに可換律が成り立つことを知っているという前提にしておきます.

 

{ \displaystyle \frac{a}{b}+\frac{c}{d}\equiv \frac{ad+bc}{bd} } は合同方程式 { \displaystyle bdx\equiv ad+bc } の解であり, これは { \displaystyle dbx\equiv cb+da } と同じです.

　この解は { \displaystyle \frac{cb+da}{db} } であり, 同じ方程式の解であることから { \displaystyle \frac{ad+bc}{bd} \equiv \frac{cb+da}{db} } , よって { \displaystyle \frac{a}{b}+\frac{c}{d} \equiv \frac{c}{d}+\frac{a}{b} } が分かります.

 

 

結合律

　続いて結合律です.

 

{ \displaystyle (\frac{a}{b}+\frac{c}{d})+\frac{e}{f} \\ \equiv \frac{ad+bc}{bd} + \frac{e}{f} \\ \equiv \frac{adf+bcf+bde}{bdf} }

{ \displaystyle \frac{a}{b}+(\frac{c}{d}+\frac{e}{f}) \\ \equiv\frac{a}{b}+\frac{cf+de}{df} \\ \equiv \frac{adf+bcf+bde}{bdf} }

 

なので { \displaystyle (\frac{a}{b}+\frac{c}{d})+\frac{e}{f} \equiv \frac{a}{b}+(\frac{c}{d}+\frac{e}{f}) } が成り立ちます.

 

　乗法についても同様です.

 

 

単位元

　加法単位元(零元)は { \displaystyle \frac{0}{b} }, 乗法単位元は { \displaystyle \frac{1}{b} } であることは直ぐに分かることでしょう.

 

　実際に各々が単位元であることもここまでくれば有理数と同じです.

　例えば零元ならば

 

{ \displaystyle \frac{0}{b}+\frac{c}{d} \equiv \frac{0d+bc}{bd} \equiv \frac{bc}{bd} }

 

, { \displaystyle \frac{bc}{bd} } は { \displaystyle bdx\equiv bc } の解ですが, { \displaystyle \text{gcd}(b,m)=1 } なのでこれは { \displaystyle dx\equiv c }, 即ち { \displaystyle x\equiv \frac{c}{d} } となるわけです.

 

　{ \displaystyle \frac{c}{d}+\frac{1}{b}\equiv \frac{c}{d} } であることは先程の可換性から明らかです.

 

　有理数は一意性が問題になってきますが, これは同値関係で解決可能です, つまり任意の有理数 { \displaystyle \frac{a}{b} } となる合同方程式は { \displaystyle bx\equiv a } ですが, この両辺に法 { \displaystyle m } と互いに素な整数 { \displaystyle k } をかけた { \displaystyle kbx\equiv ka } もまた { \displaystyle \frac{a}{b} } の解であるため, これを同一視するわけです.

 

　言うなれば, 有理数を既約分数で解釈するようなものです.

　従って任意の有理数はその既約分数となりうる数を代表元とすれば問題ありません.

 

　そういう意味では, 加法単位元は { \displaystyle \frac{0}{1} }, 乗法単位元は { \displaystyle \frac{1}{1} } とするべきでしょうか.

 

 

逆元

　{ \displaystyle \frac{a}{b} } に対する加法逆元(反元)は { \displaystyle \frac{-a}{b} }, 乗法逆元は { \displaystyle \frac{b}{a} } (但し { \displaystyle a\neq 0 } ) であることも明らかでしょう.

 

　加法逆元について説明すれば,

 

{ \displaystyle \frac{a}{b}+\frac{-a}{b} \equiv \frac{ab-ab}{b^2} \equiv \frac{0}{b^2} }

 

となります.

　先程の単位元のくだりの通り, { \displaystyle \frac{0}{b^2} } は { \displaystyle \frac{0}{1} } と合同なのでちゃんと単位元となっています.

 

　乗法についても同様です.

 

 

 

　以上により, { \displaystyle (M,+), (M,\times ) } はそれぞれアーベル群, 可換乗法群であることが分かりました.

 

 

分配律

　ここから「環」の定義を満たすかどうかになります.

　以降では { \displaystyle (M,+,\times ) } を { \displaystyle M } と略記します.

　まず分配律ですが,

 

{ \displaystyle \frac{a}{b}(\frac{c}{d}+\frac{e}{f}) \\ \equiv\frac{a}{b}\times\frac{cf+de}{df} \\ \equiv\frac{acf+ade}{bdf} }

{ \displaystyle \frac{a}{b}\frac{c}{d}+\frac{a}{b}\frac{e}{f} \\ \equiv \frac{ac}{bd}+\frac{ae}{bf} \\ \equiv \frac{acf+dae}{dbf} \\ \equiv \frac{acf+ade}{bdf} }

 

なので成り立ちます.

　{ \displaystyle (\frac{a}{b}+\frac{c}{d})\frac{e}{f}=\frac{a}{b}\frac{e}{f}+\frac{c}{d}\frac{e}{f} } も同様に確かめられます.

 

　よってこの時点で { \displaystyle M } は環であることが分かります.

 

 

単位的環

　環が単位的環になるには { \displaystyle M\neq\emptyset } が { \displaystyle 0 } でない乗法単位元を持つことですが, これは単位元の項で既に確認済です.

 

　…と言いたいんですが件では零元しか確認してませんでしたので折角なのでこちらで書いておきましょう.

 

{ \displaystyle \frac{1}{1}\times\frac{c}{d} \equiv \frac{1c}{1d} \equiv \frac{c}{d} }

 

, 同様に { \displaystyle \frac{a}{b}\times\frac{1}{1} \equiv \frac{a}{b} } であることも直ちに導かれます.

 

 

斜体

　ここからは「体」のカテゴリになります.

　斜体とは, 単位的環の任意の元 { \displaystyle a\neq 0 } が正則であることを言います.

　言い換えれば, 任意の元 { \displaystyle a\neq 0 } について { \displaystyle aa'\equiv 1 } なる元 { \displaystyle a' } が存在することを言います.

　しかしこれは有理数表示の定義そのものなので成り立つことは明らかですね.

 

 

体

　斜体 { \displaystyle M } が乗法可換であるとき, { \displaystyle M } は体と言います.

　乗法可換は既に分かっているので, これで晴れて { \displaystyle (M,+,\times ) } が体であることが分かりました.

 

　これで, 減法・除法をそれぞれ

 

{ \displaystyle \frac{a}{b}-\frac{c}{d} :\equiv \frac{a}{b}+\frac{-c}{d} }

{ \displaystyle \frac{a}{b}\div \frac{c}{d} :\equiv \frac{a}{b}\times(\frac{c}{d})^{-1} }

 

とすれば四則演算すべてOKということになります.

 

 

〆

　因みに　{ \displaystyle (M, +,\times ) } はこの他

 

  • 可換環
  • 整域

 

でもあるんですが, 体を導くにあたって必須ではないので省略しました.

 

 

thetheorier