こんにちは, @the_theorierです.
昨日, 今朝とユークリッドの互除法について紹介しましたが, 書き終わってふと思い立ったのでちょっと調べてみました.
式変形は何回で終わるのか
正の整数 a, b (a>b, b>0) を任意に取ってきて, それを a = bq + r と分解する操作を繰り返すことで a, b の最大公約数を得るのがユークリッドの互除法ですが, この式変形は a, b の値によって何回で済むでしょう?
昨日書いた互除法の説明では「高々 b 番目」と書きましたが, 実際にはそれよりももっと少なく, 多くても [b/2] 回を下回ると思われます([・]はガウス記号).
まず話を円滑にするために, 一通りの「傾向」「取り決め」を明らかにして, より簡単な範囲で検証を行うことにします.
まず一つ目としては, 検証する a は次の法bによる剰余類から自明である a = b を取り去った
b+1, b+2, …, 2b-1
だけで十分であることが分かります.
というのも, この前後は a = bq + r と分解するときに q を増減させるだけで済むからです, 「剰余類」をご存じの方であれば尚更言うまでも無いことです.
そういう意味では a = b+1 も殆ど明らかなのですが, 一応入れておきます.
また, 対象となる a, b での式変形の回数を #[a, b] と表します.
例えば a=5, b=3 なら
5 = 3×1 + 2
3 = 2×1 + 1
(2 = 1×2)
なので, #[5, 3] = 2 となります.
調べてみた
取り敢えず b = 20 までを調べてみました, 手計算なので間違いがあるかもしれません.

縦が a, 横が b になります.
ボーっと見ていると法則が見られる部分がチラホラとあるにはあるようですね.
簡単に見つけたものだけを, 簡単なものから「そんな感じ」なものまで書いておきます.
[1]
任意の正整数 n について,
#[n+1, n] = 1
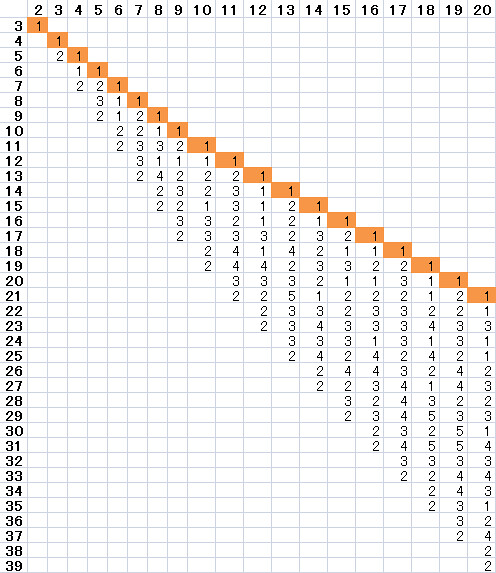
※対象の部分をオレンジで塗ってます, 以下同様
これはもう明らかと言うしかないですね.
n+1 = n + 1
( n = n×1 )
で完結するので, 1回となります.
[2]
n≧2 なる任意の整数について,
#[2(n+1), 2n] = 1

これも
2(n+1) = 2n + 1
( 2n = (2n)×1 )
となるので1回です.
[3]
n≧3 なる任意の整数について
#[2n-1, n] = 2

これも
2n-1 = n + (n-1)
n = (n-1) + 1
( n-1 = (n-1)×1 )
となるので2回ですね.
[4]
n≧2 なる任意の整数について
#[4n, 2n+1] = 3

これは
4n = (2n+1) + (2n-1)
2n+1 = (2n-1) + 2
2n-1 = 2×(n-1) + 1
( n-1 = (n-1)×1 )
となることから3回であると分かります.
[5]
n≧3 なる任意の整数について
#[4n-2, 2n] = 2

これは
4n-2 = 2n + (2n-2)
2n = (2n-2)×1 + 2
( 2n-2 = 2×(n-1) )
となることから2回ですね.
[6]
以降は「傾向」です, しっかりとした推論すらしてないので間違いがあるかもしれません.
言ってみれば[1]~[5]は図からすれば「外側」だけであり, 後は「内側」が問題になってきます.
その内側について「こうだろうなぁ…」と思ったのは3点あり, a, b をそれぞれ素因数分解したときの各素因数の「分布」と「共通」の具合によるものです, 具体的には
- 共通する要素が多い
- a側とb側の要素の散らばりが少ない(両方の要素が出来るだけ小さい区間に収まっている)
- 互いの要素の集まりが相対的に孤立していない
, この3つがより当てはまるほど, 回数 #[a, b] が少ない傾向にあるようです.
いくつか例を挙げて観察しましょう.
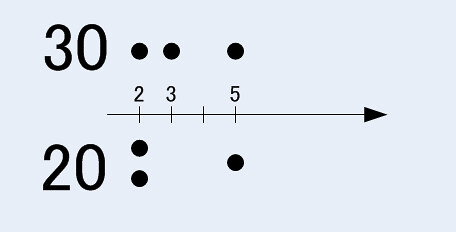
(cf. 1) a=30, b=20
この場合,
30 = 20 + 10
( 20 = 10×2 )
なので #[30, 20] = 1 ですね.
30, 20 を素因数分解するとそれぞれ 30 = 2×3×5, 20 = 22×5 であり, 30側の素因数の要素は2, 3, 5 が一つずつ, 対して20は2が2つと5が1つで, それぞれをグループとして見ると互いはかなり密接しています.
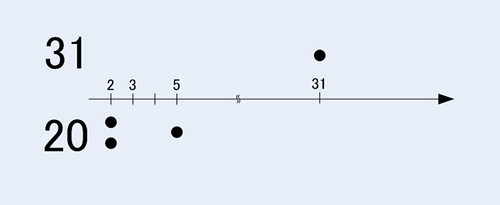
(cf. 2) a=31, b=20
先程に比べ a が1増えた状態ですね, この場合
31 = 20 + 11
20 = 11 + 9
11 = 9 + 2
9 = 2×4 + 1
( 2 = 1×2 )
となるので #[31, 20] = 4, 4回もかかります.
それぞれ素因数分解すると, 31はそのまま, 20は先程と同じで 20 = 22×5 です.
それぞれを要素とする集合として見ると, 31側と20側はかなり離れて分布しています.
(cf. 3) a=25, b=18
この場合はどうなるでしょう?まず回数を調べると
25 = 18 + 7
18 = 7×2 + 4
7 = 4 + 3
4 = 3 + 1
( 3 = 1×3 )
となるので #[25, 18] = 4, こちらも4回かかりますね.
では素因数分解してみましょう, 25 = 52, 18 = 2×32 ですから分布は下のようになります.
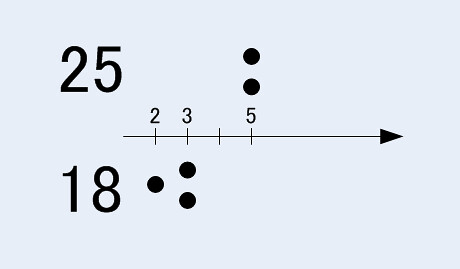
傍目からは密接しているように見受けられますが, 相対的には各々が集合として「狭い」ために, 相対的に互いに孤立しているため, 回数が多いと思われます.
余り (cf. 1) と変わらないように見えますが, これは一つ目の推論である「共通する要素が多い」かどうかが影響しているのでしょう.
〆
まぁこんなことが分かったからって得をする人がいるかは分かりませんけどねw
一応需要が無いとは思いません, 例えば問題を作る人とか.
あんまり計算量が少ないのにしてしまったら簡単すぎでダメですし.
あ, まだ早いですけど夏休みの研究のネタにするとかね.
