もう一人のY君

iPhoneアプリのレビューやアップデートレビューなどを書いています. たまに数学の記事も書きます.

もう一人のY君　MENU 　MENU

【ショートカット】arctanの近似値を計算する

iOS iOS-iOS12 iOS-ショートカット

181215_03

　今回は三角関数の一つであるtanの逆関数 arctan を計算します.

 

ショートカット

ショートカット

  • Apple
  • 仕事効率化
  • 無料

※価格は記事執筆時のものです. 現在の価格はApp Storeから確認ください.

　レビュー時のバージョン　：　v2.1.1

 

スポンサーリンク

 

 

ないなら作るしかない

　arctanは座標系の点から距離と角度を求める際の後者に相当するため, 数学はもちろんですが物理学や航空学などで重宝されます.

 

　しかし現時点で三角関数は通常の3つしか用意されていません.

　それらから各種逆関数は作れませんし他のアクションを利用して「正しいarctan」を作ることはできないため, 我々ができることは近似値を得ることです.

 

 

arctan近似式 - 風の迷路

ルジャンドル多項式 を利用して、定積分を求めるガウス求積という方法を使えるようになりました。 これを利用して、アークタンジェントの近似式を作ります。 アークタンジェントは、1／（1＋x^2）の積分で求まり、 ３次のルジャンドル多項式を利用し...

　近似式についてはルジャンドル多項式を用いたこちらのサイトさんのものを参考にします.

　件のサイトさんでは「計算のしやすさ」を重んじて最終的に

 

{ \displaystyle \arctan{x}\approx \frac{75x^2+285}{3x^2+5}x }

 

としていますが, ショートカットではそんな配慮は無用ですからもうちょっと精度の良い数式にし,

 

{ \displaystyle \arctan{x}\approx \frac{76.39437x^2+286.47889}{3x^2+5}x }

 

とします.

 

　またサイトにもある通り, { \displaystyle |x|\leq 1 } の場合は { \displaystyle \arctan{x} = \frac{\pi}{2} -\arctan\left(\frac{1}{x}\right) } を用います.

　もちろん度数法の場合は { \displaystyle \frac{\pi}{2} } でなく { \displaystyle \frac{180}{2}=90 } となります.

 

　…と, これで良いと思いたかったのですが, 検証の結果 { \displaystyle |x|\leq 1 } の場合ははじめの計算式のほうが精度が良かったため, 条件に応じて使い分けることにしました.

 

 

フロー

　なお今回はラジアンでなく度数法を採用します, ラジアンの場合も同じく上記サイトで紹介されています.

　また計算式は関数としてメインから分けて作成しました.

 

　まずはメインからです.

 

 

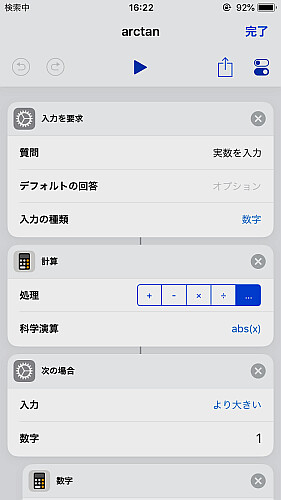
181215_04

　まず { \displaystyle \arctan{x} } の変数 { \displaystyle x } を与えます.

　{ \displaystyle x } が負数である場合を想定し, { \displaystyle |x|\gt 1 } かどうかで場合分けします.

 

 

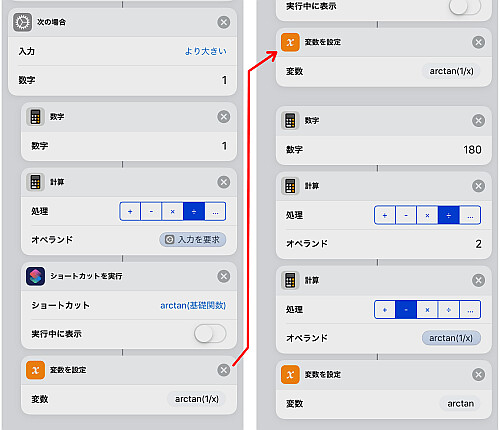
181215_05

　{ \displaystyle |x|\gt 1 } の場合は先程の通り { \displaystyle \arctan{x} = \frac{\pi}{2}-\arctan{\left( \frac{1}{x} \right)} } の式を適用します.

　{ \displaystyle x } の逆数を取ってから計算式の関数(後述)を適用し, { \displaystyle \frac{180}{2} = 90 } から今得た値を引きます.

 

 

181215_06

　同じ条件下に加えて { \displaystyle x\lt 0 } である場合は得た数を { \displaystyle 180 } から引きます.

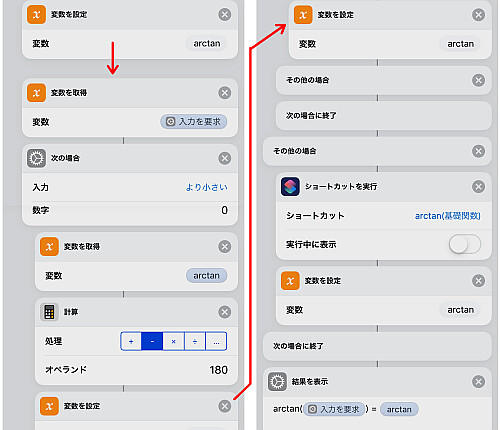
　「次の場合」のその他である { \displaystyle |x|\leq 0 } の場合は変数 { \displaystyle x } にそのまま計算式の関数を当てるだけです.

　最後に「結果を表示」などでそれなりの体裁で表示します.

 

 

関数

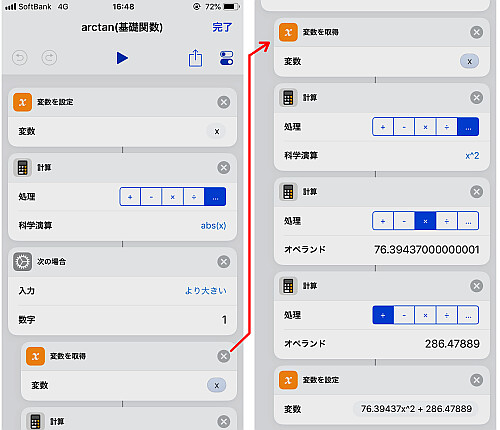
181215_07

　続いて計算式本体の関数です.

　今回は一次変数式のため関数を呼び出した際の値をそのまま「変数を設定」で取り込みます.

　得た値 { \displaystyle x } が { \displaystyle |x|\gt 1 } を満たす場合,

 

{ \displaystyle \arctan{x}\approx \frac{76.39437x^2+286.47889}{3x^2+5} }

 

を適用します(画像では分子の部分まで計算しています.).

 

 

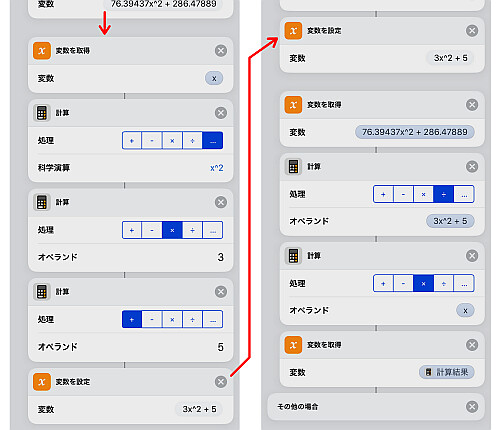
181215_08

　分母に相当する { \displaystyle 3x^2+5 } を計算し, 先程作った分子から割ります.

 

 

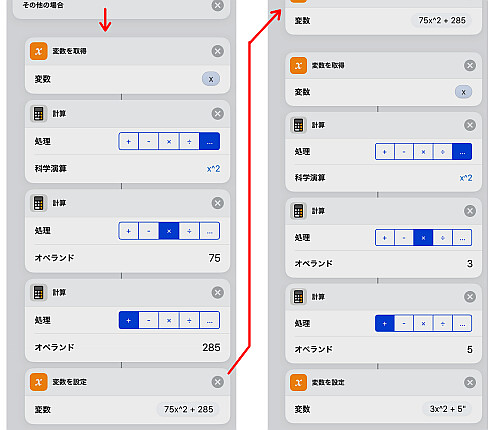
181215_09

　「次の場合」の「その他の場合」に相当する { \displaystyle |x|\leq 1 } の場合は

 

{ \displaystyle \arctan{x}\approx \frac{75x^2+285}{3x^2+5} }

 

を用います.

　分母・分子の部分をそれぞれ計算し,

 

 

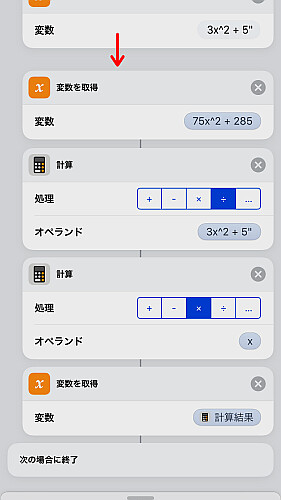
181215_10

　分子から分母を割って計算式を得ます.

　「変数を取得」は今回は必須ではありません.

 

 

実行

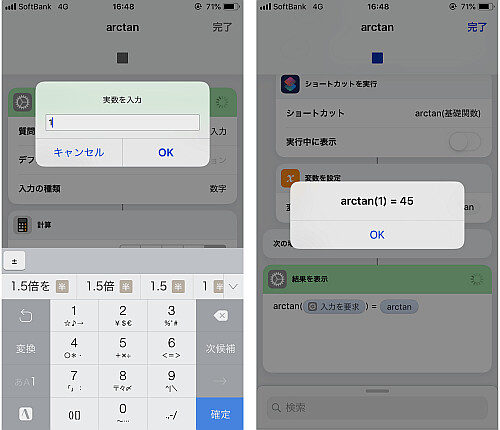
181215_11

　実際に実行して結果を確かめます.

 

 

181215_12

　まったく精度の高い式ではないため多少の誤差は存在します.

 

 

誤差

　なおいくつかの値による誤差などは下の通りです.

変数  近似値  正値  誤差(絶対値) 
0.01  0.56998  0.57293  0.00295 
0.1  5.68091  5.71059  0.02968 
0.5  26.41304  26.56505  0.15201 
1  45  45  0 
5  78.75  78.69006  0.05994 
10  84.31908  84.28940  0.02968 
20  87.15239  87.13759  0.01480 
50  88.86015  88.85423  0.00592 
100  89.43001  89.42706  0.00295 
200  89.71500  89.71352  0.00148 
500  89.88600  89.88540  0.00060 
1000  89.94300  89.94270  0.00030 

 

　{ \displaystyle |x| } が大きければ大きいほど, 誤差が小さくなるのは自然なことです.

　大きな誤差で約 { \displaystyle 0.152 } となりました, 精度を重んじる用途ではこの誤差は大きいですね.

 

 

thetheorier