もう一人のY君

iPhoneアプリのレビューやアップデートレビューなどを書いています. たまに数学の記事も書きます.

もう一人のY君　MENU 　MENU

【数学】確率のパラドックス

数学

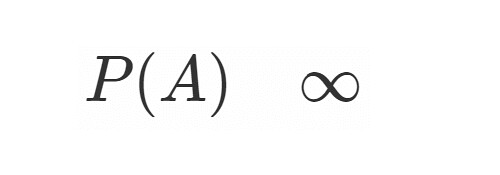
instinct probability

　当たり前のように思えるそれが, ある条件を満たすと覆ってしまうのは数学ではよくあります.

 

 

スポンサーリンク

 

 

直感的な「確率」

　一般に理解されている「確率」と言えば以下のような表現でしょう.

 

 

[定義：直感的確率]

　全事象 { \displaystyle \Omega } とその部分集合 { \displaystyle A }, 根源事象 { \displaystyle N } とし, { \displaystyle A } や { \displaystyle N } などが起こりうる数を { \displaystyle n(A), n(N) } などと書くことにすると, { \displaystyle A } が起こる確率 { \displaystyle P(A) } は

 

{ \displaystyle P(A)=\frac{n(A)}{n(N)} }

 

　多少の表現の違いこそあれ, こういうイメージであろうと思います.

 

 

無限集合でも成り立つか

　では上のような定義は無限集合であっても通用するのでしょうか？

 

　試しに以下のように定義してみましょう.

　{ \displaystyle A } は自然数 { \displaystyle \mathbb{N} } の部分集合とし, { \displaystyle \mathcal{A} } を { \displaystyle A } のクラス(分からなければ集合を要素とする集合でも良いです)以下を満たすようなものとします.

(厳密にはクラスは「集合を要素とする集合」ではありません)

 

{ \displaystyle \mathcal{P}(A):=\lim_{n\to\infty}\frac{^{\#}\{m\mid 1\leq m\leq n,\,m\in A\}}{n} }　…(1)

( { \displaystyle  ^{\#}\{S\} } は集合 { \displaystyle S } の要素の個数のことです)

 

　{ \displaystyle A_n=\{1,2,\dots ,n\} } とすると, 以下が成り立つことがわかります.

 

　任意の { \displaystyle n\in\mathbb{N} } について

  1. { \displaystyle A_n\in\mathcal{A} }
  2. { \displaystyle A_n\subseteq A_{n+1} }
  3. { \displaystyle \cup_{n\in\mathbb{N}}A_n = \mathbb{N} }

 

 

　さて,

 

{ \displaystyle ^{\#}\{m\mid 1\leq m\leq n \}=m }

 

であることから任意の自然数 { \displaystyle m } について

 

{ \displaystyle \mathcal{P}(A_m)=\lim_{n\to\infty}\frac{m}{n}=0 }

 

が言えます.

 

　一方 { \displaystyle \cup A_n=\mathbb{N} } でしたから,

 

{ \displaystyle \mathcal{P}(\mathbb{N})=1 }

 

であるはずです.

 

　このように, 演算の順序によって得られる値が変わってしまいます.

 

 

〆

　アキレスと亀などをはじめ, 我々が日常的にイメージしたり直感的にこうであると思っていることは, 無限という概念が絡むと簡単に崩壊してしまうんですね.

 

　結果, 今回定義した「確率のようなもの」は(公理的)確率論における確率空間を満たしていないことになります.

 

thetheorier